Презентація "Перпендикулярність прямих у просторі"
Про матеріал
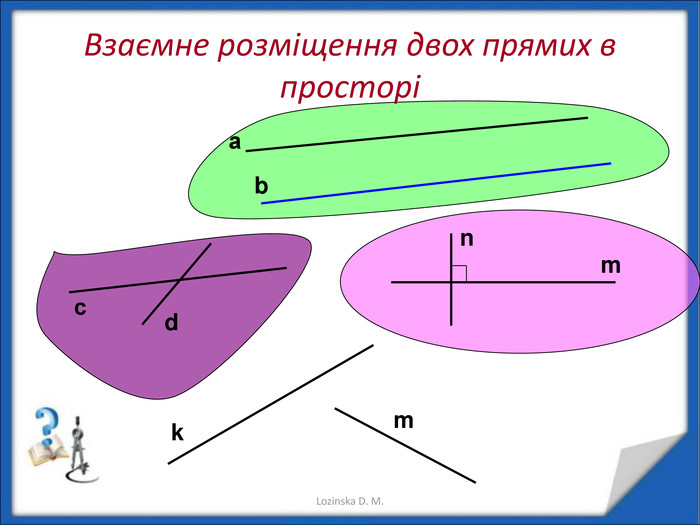
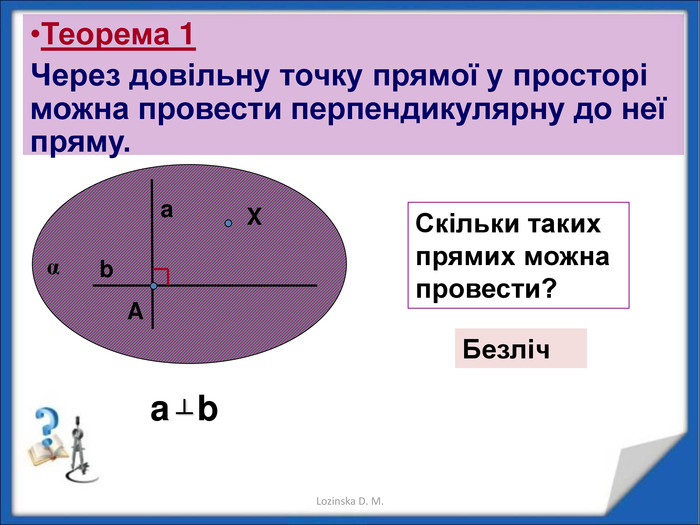
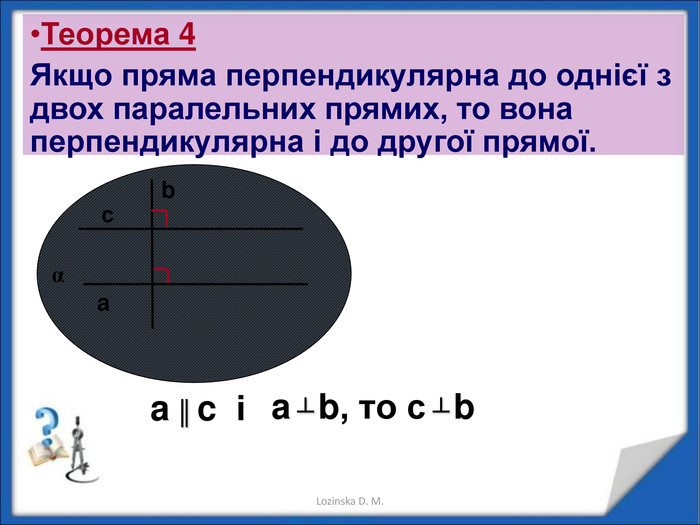
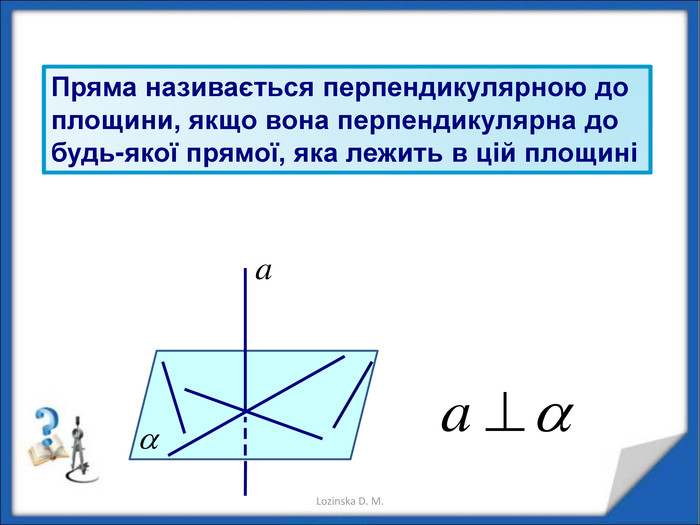
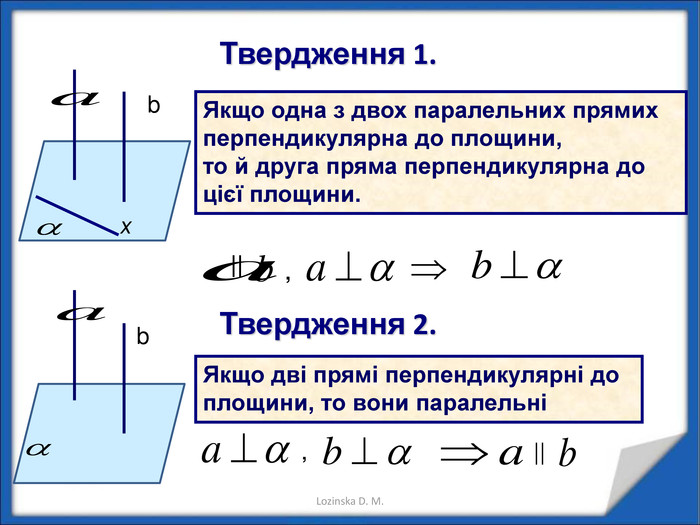
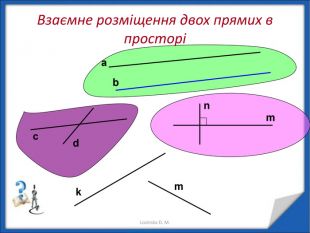
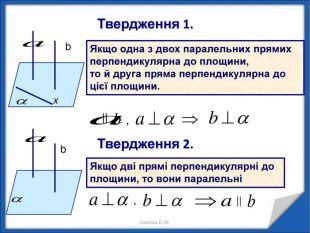
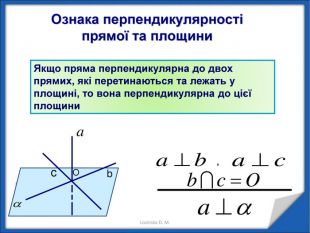
Перпендикулярність прямих у просторі.
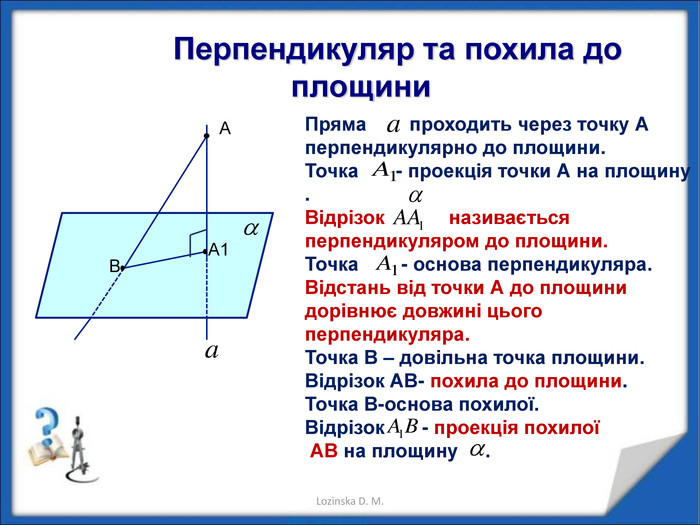
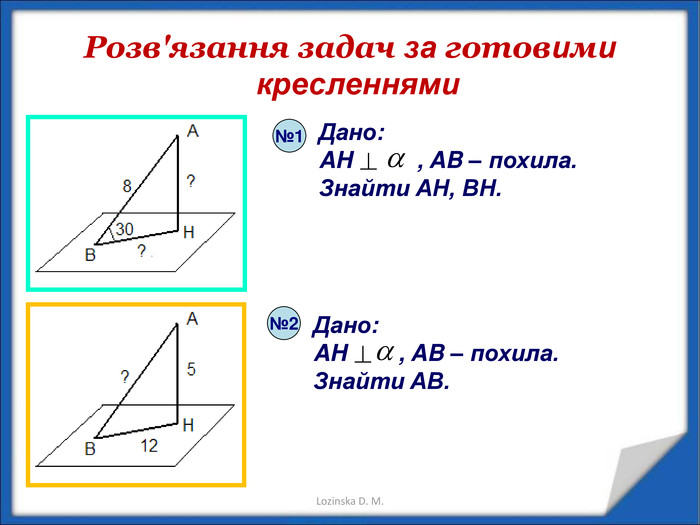
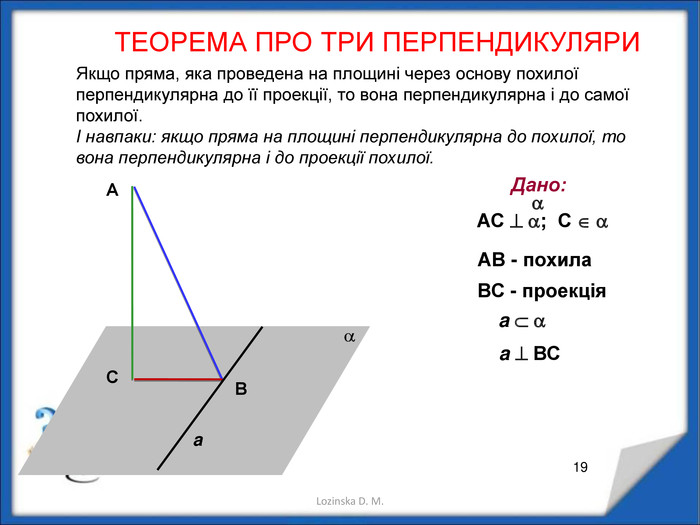
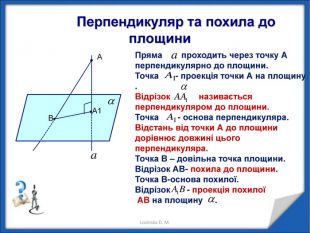
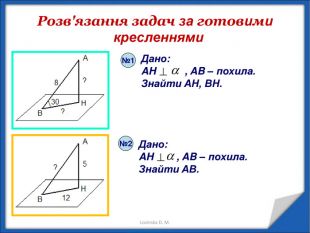
Перпендикулярність прямої і площини. Перпендикуляр і похила. Теорема про три перпендикуляри Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

























-

Гура Олена Федорівна
14.11.2024 в 08:55
Чудовий, змістовний матеріал гарно оформлений. Респект.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
27.11.2023 в 16:17
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мольцан Вікторія Іванівна
06.11.2023 в 17:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Tokar Svetlana
12.04.2022 в 15:31
Загальна:
1.3
Структурованість
1.0
Оригінальність викладу
2.0
Відповідність темі
1.0
Показати ще 1 відгук