Презентація "Площа многокутника. Площа прямокутника, паралелограма"
Про матеріал
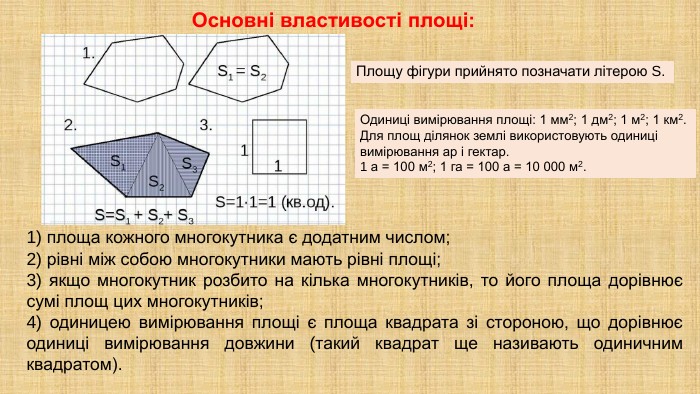
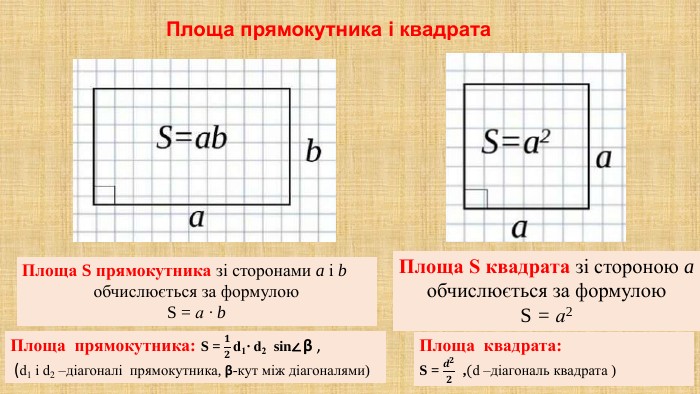
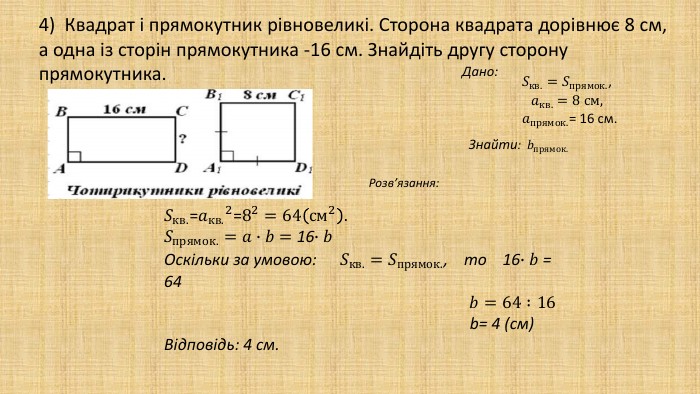
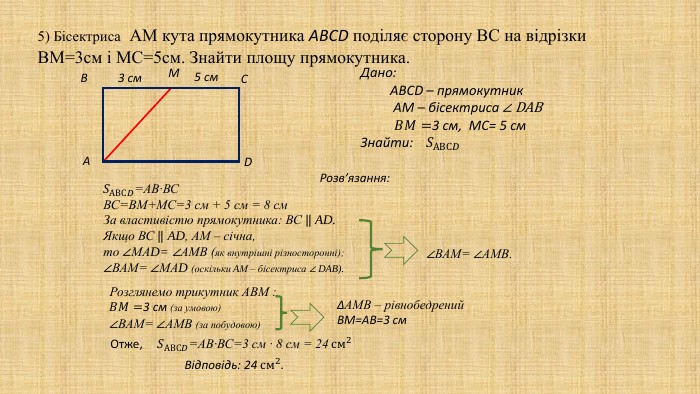
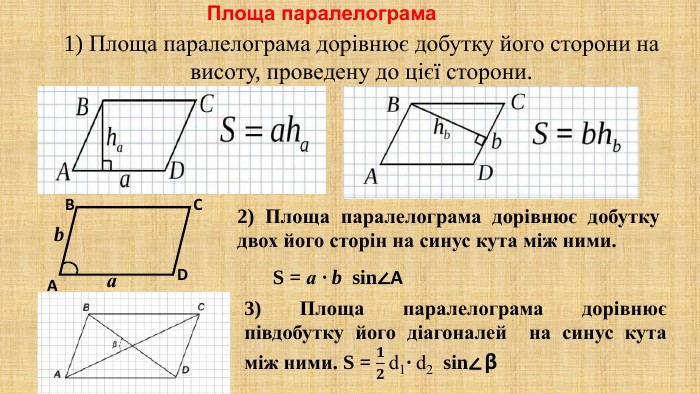
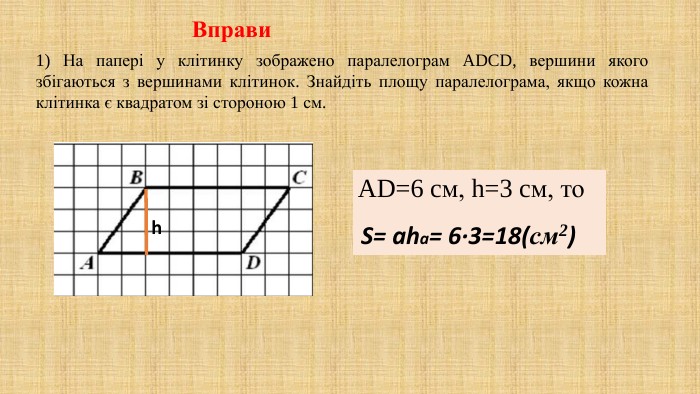
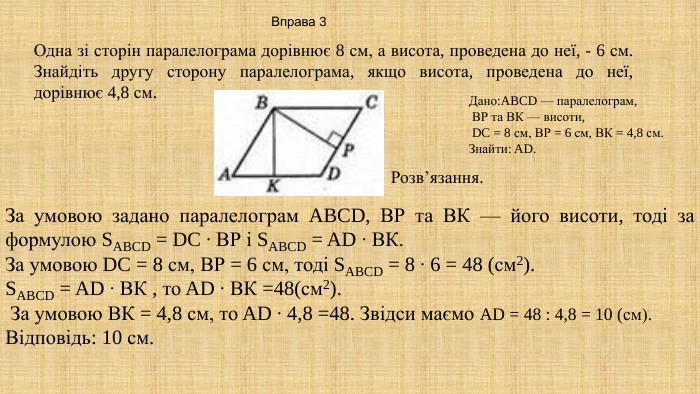
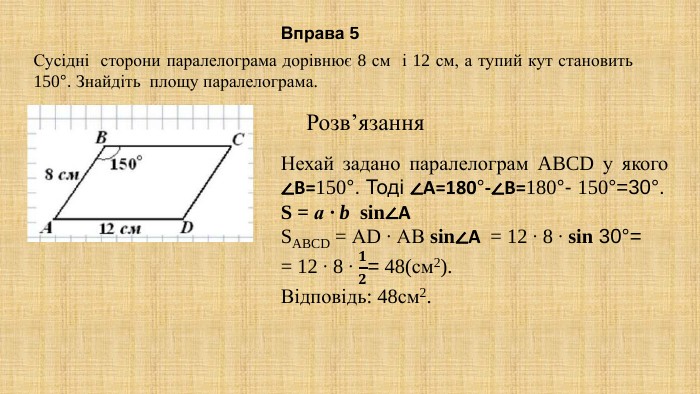
Презентація "Площа многокутника. Площа прямокутника, паралелограма" для здобувачів освіти, які вивчають геометрію у восьмому класі. В презентації дано поняття площі, властивості площі, формули для знаходження площі прямокутника, квадрата, паралелограма та ромба,а також представлено готові розв'язані задачі на застосування формул знаходження площі фігур. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
От в таких презентаціях і показана краса геометрії!
-
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку