Презентація "Площа трикутника"
Про матеріал
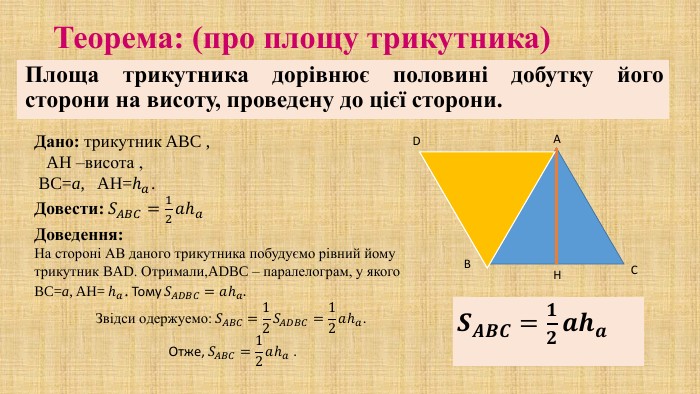
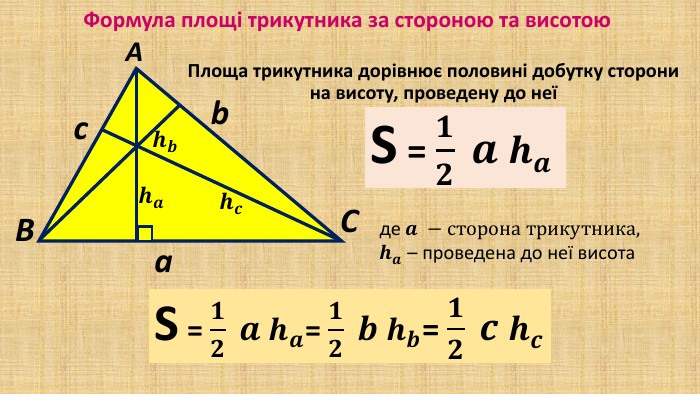
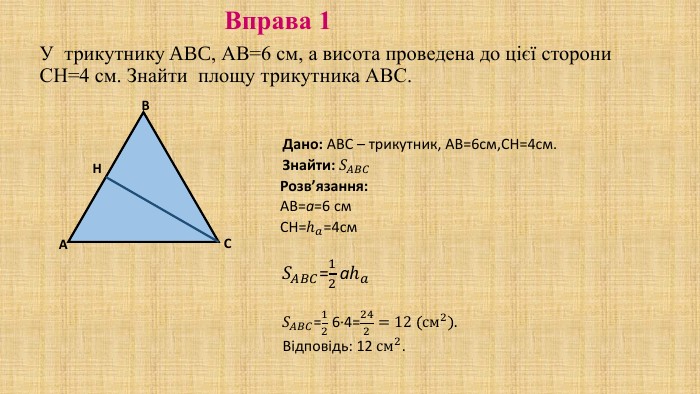
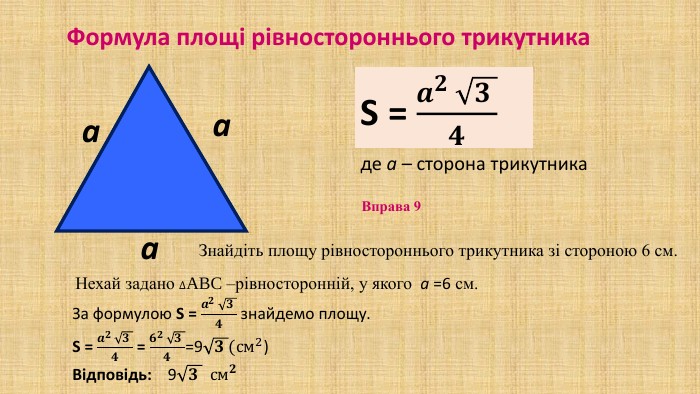
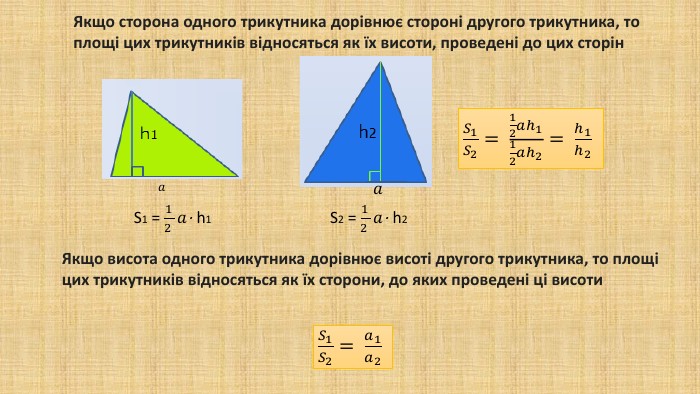
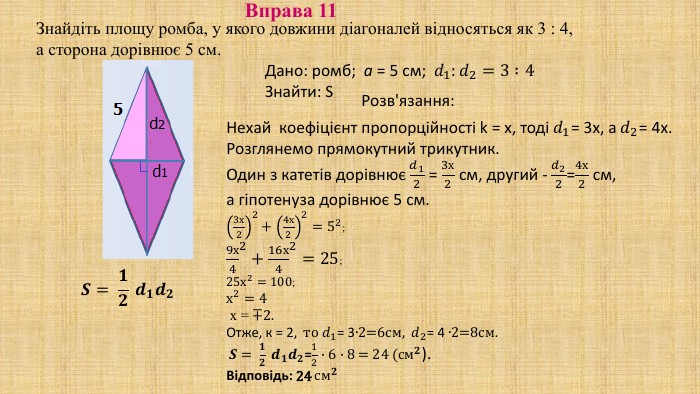
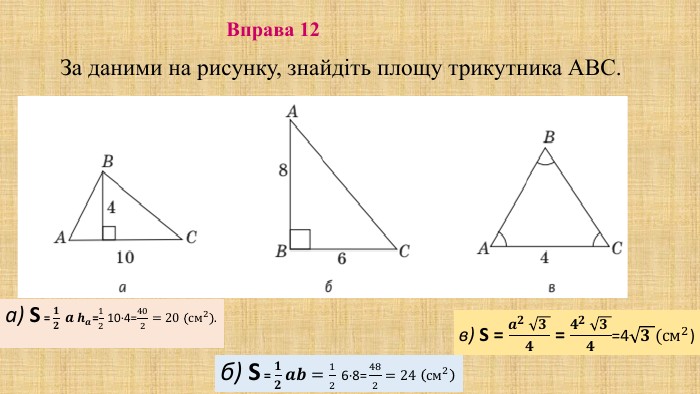
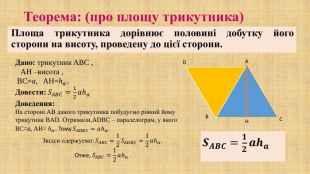
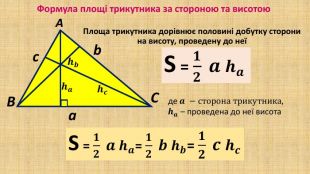
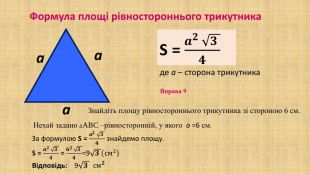
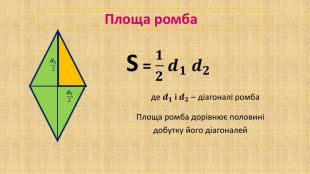
Презентація "Площа трикутника" для здобувачів освіти, які вивчають геометрію у восьмому класі. В презентації дано формули для знаходження площі трикутника, різних видів та за допомогою різних формул, а також представлено готові розв'язані задачі на застосування формул знаходження площі трикутника. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Перепелиця Тетяна Іванівна
11.02.2025 в 23:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іванютіна Вікторія Миколаївна
03.04.2024 в 11:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шидловська Антоніна Сергіївна
29.01.2024 в 02:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Томилова Тамара
03.11.2023 в 20:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
16.05.2023 в 22:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Коляденко Антоніна
12.05.2023 в 09:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
11.05.2023 в 10:43
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Siriachenko Svitlana
02.05.2023 в 22:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Роенко Наташа
19.04.2023 в 06:04
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
07.04.2023 в 09:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кіріяк Наталія
06.02.2023 в 19:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Отдатчикова Людмила Миколаївна
06.05.2022 в 06:04
Дуже гарно і повно відображена тема
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 9 відгуків