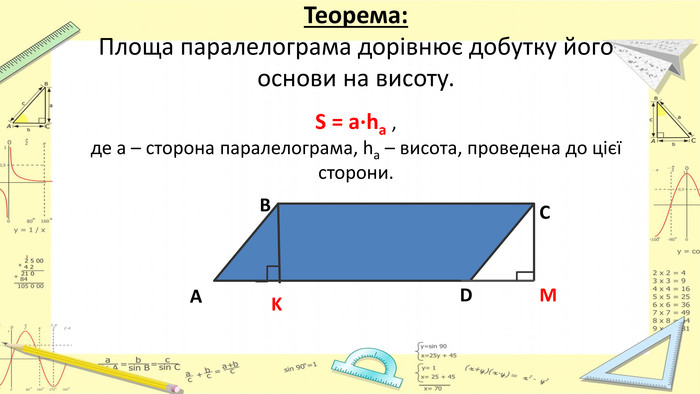
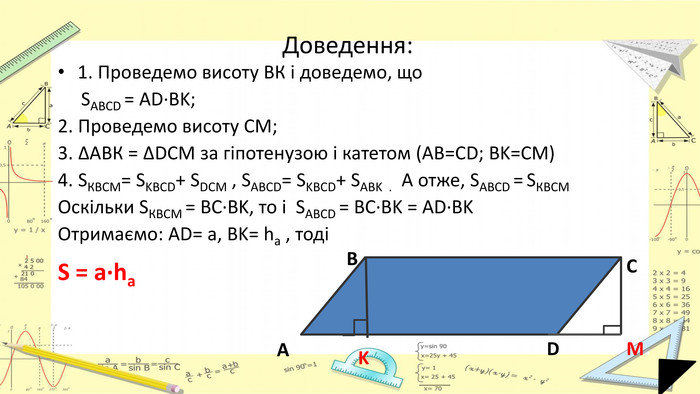
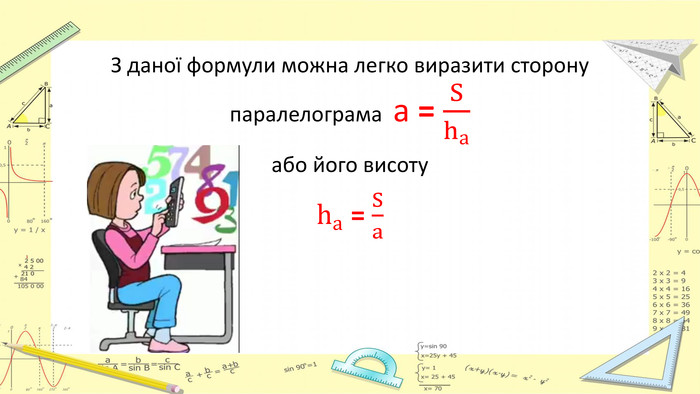
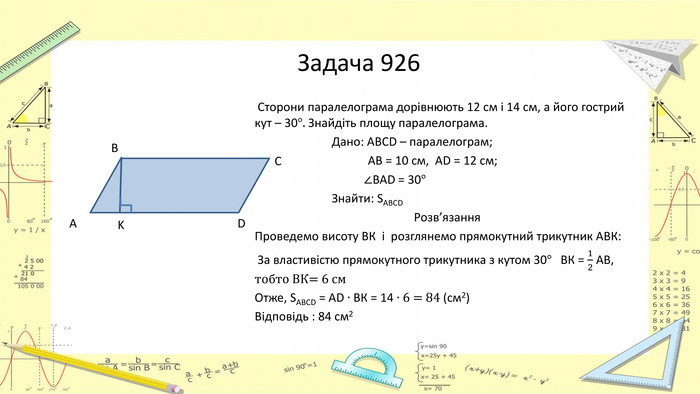
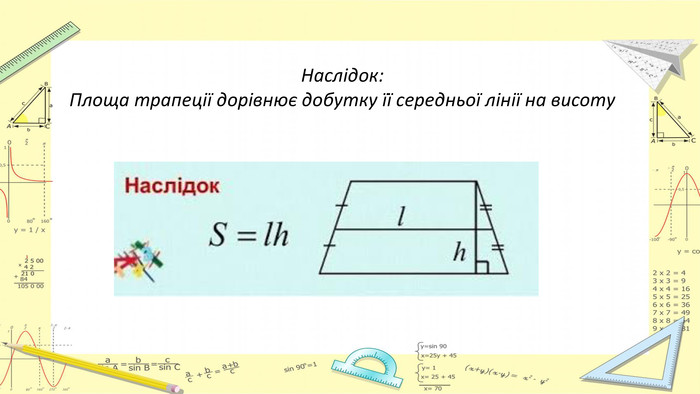
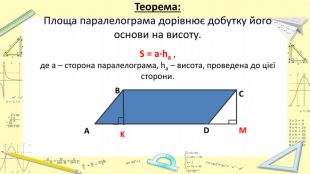
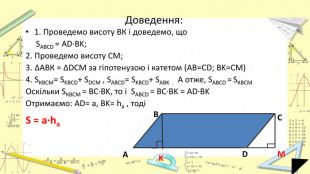
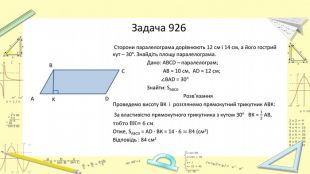
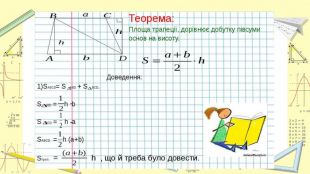
Презентація "Площі паралелограма і трапеції"
Про матеріал
Презентація "Площі паралелограма і трапеції" допоможе учням краще зрозуміти дану тему. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку