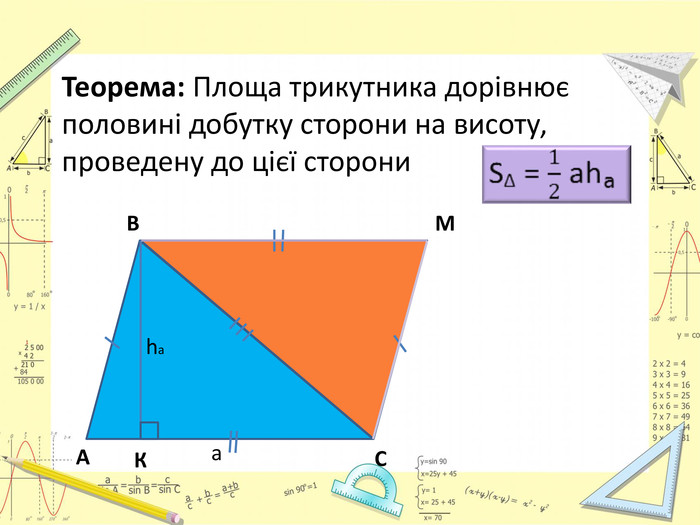
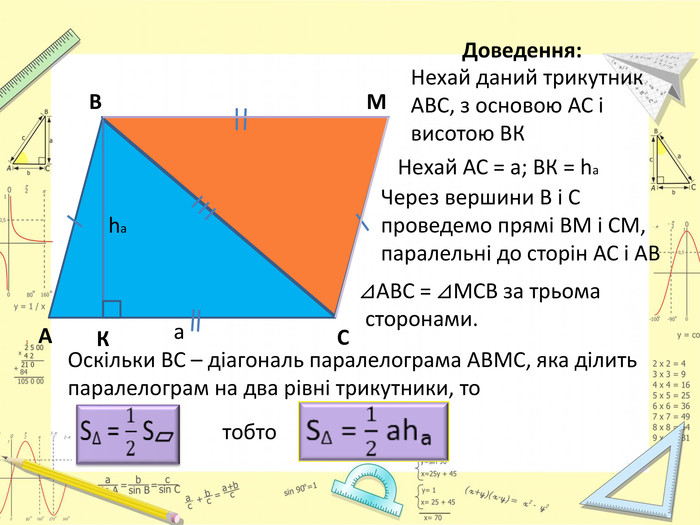
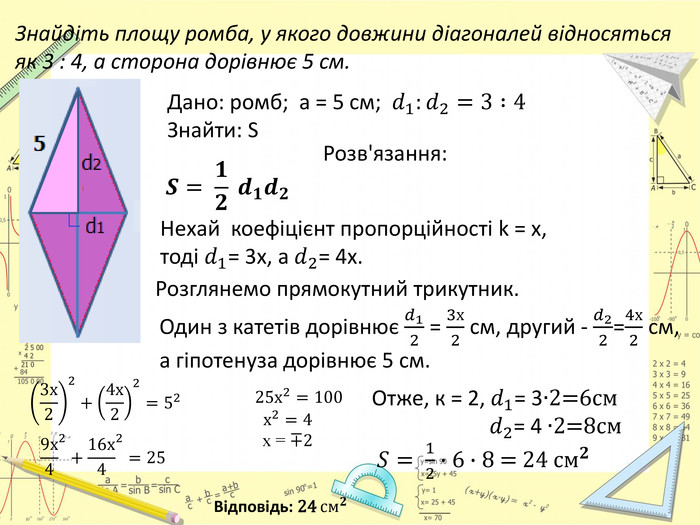
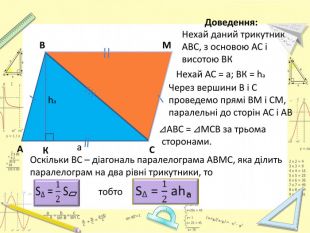
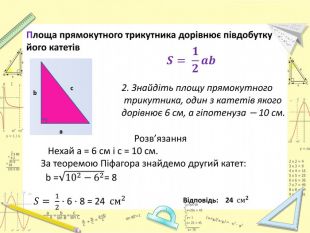
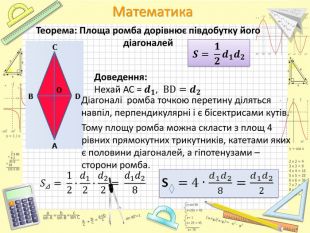
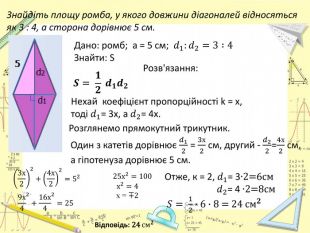
Презентація "Площі трикутника і ромба"
Про матеріал
Презентація "Площі трикутника і ромба" дасть змогу краще зрозуміти дану тему і легко запамятати Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку