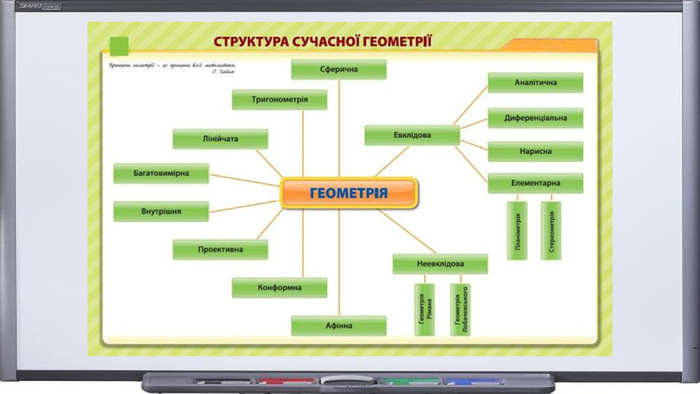
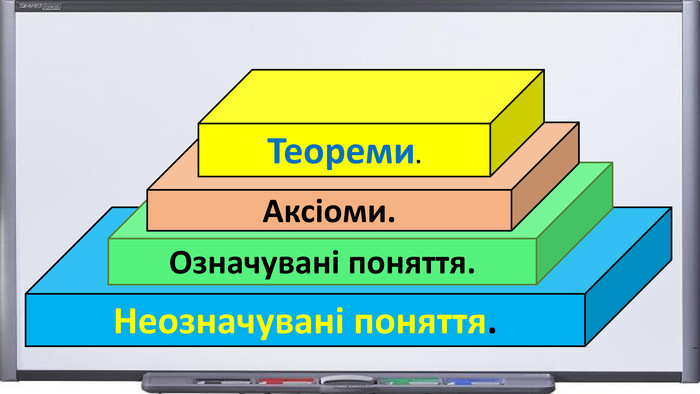
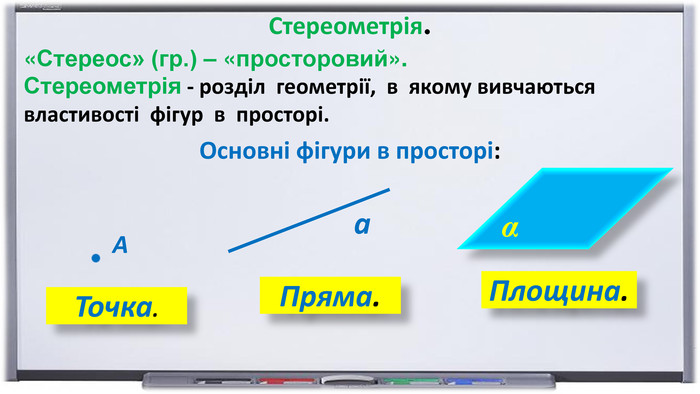
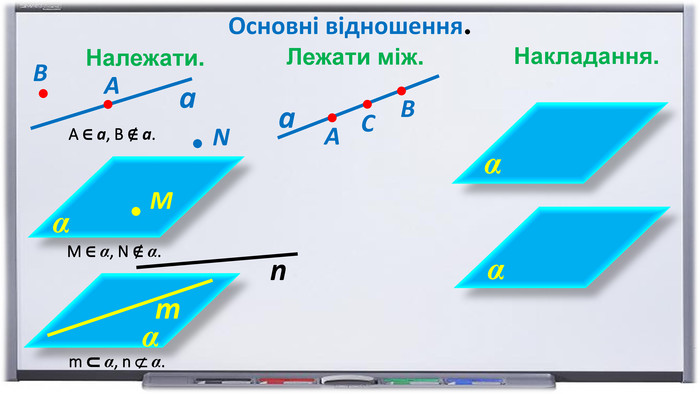
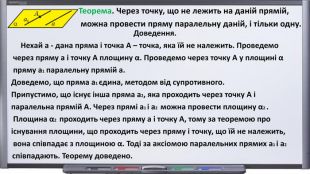
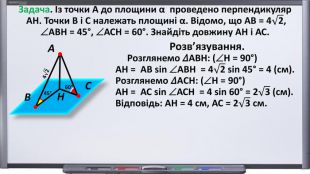
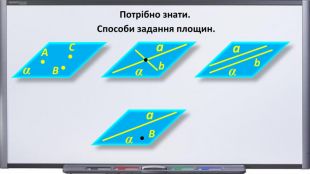
Презентація. "Початкові відомості зі стереометрії. Аксіоми та теореми стереометрії. Прямі і площини в просторі".
Про матеріал
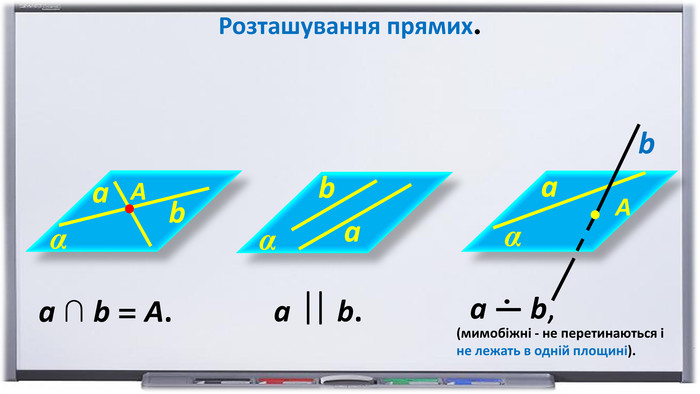
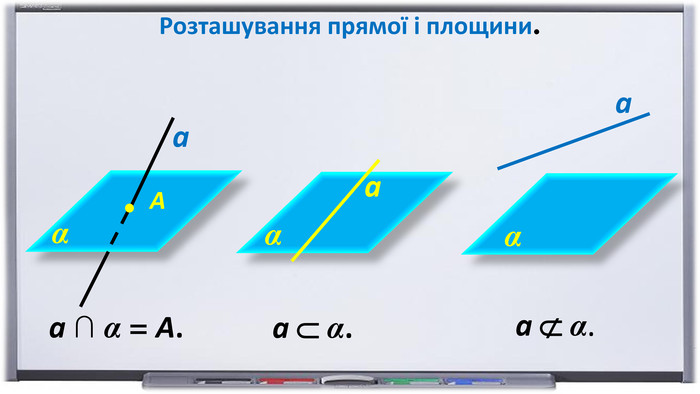
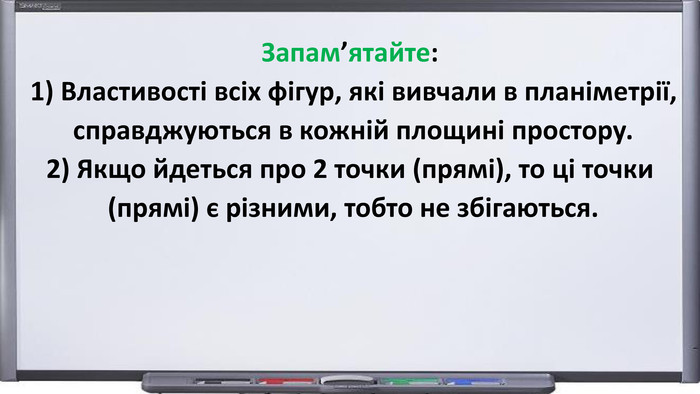
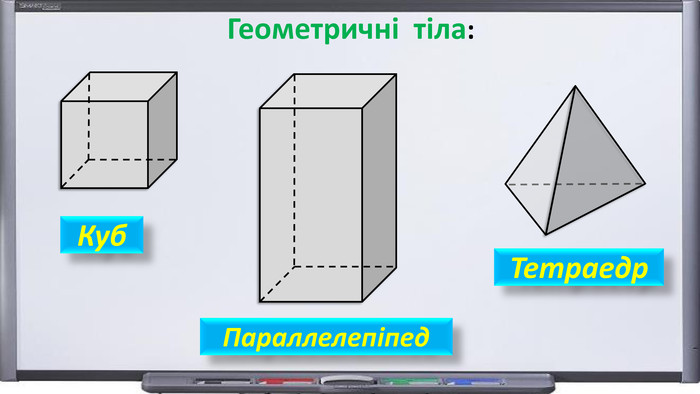
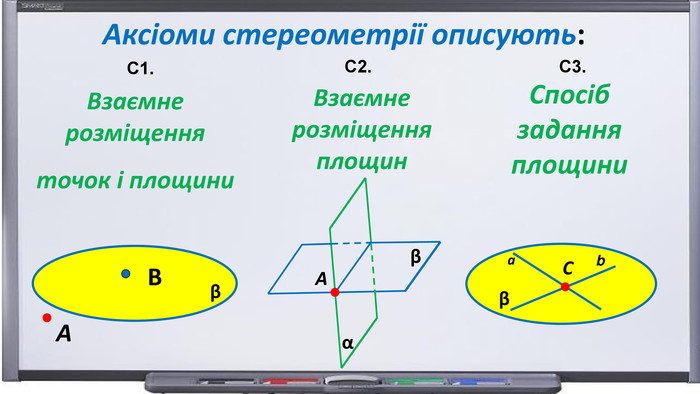
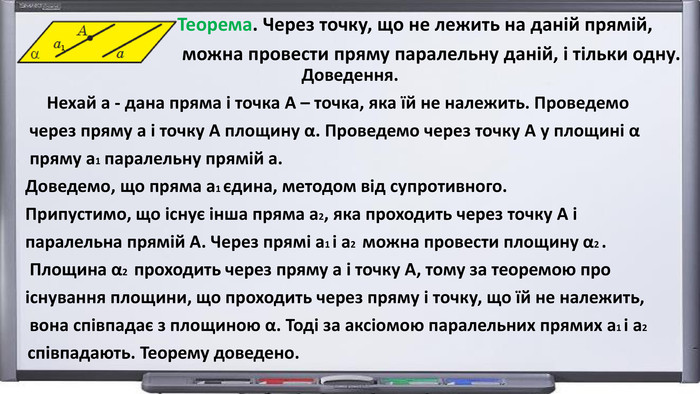
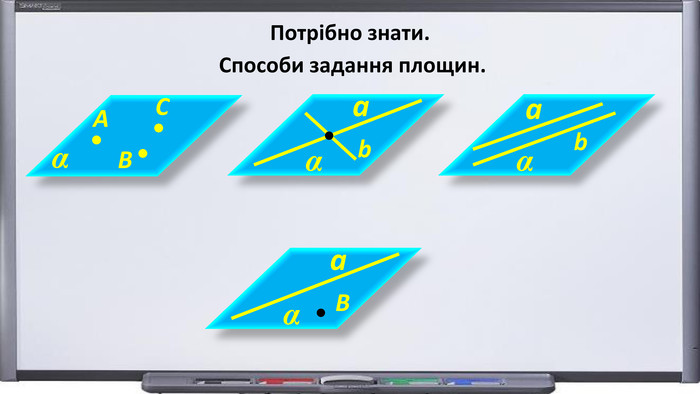
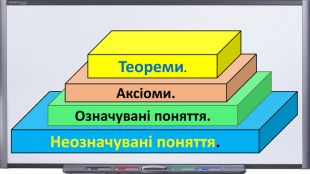
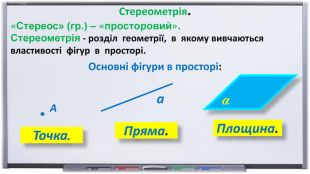
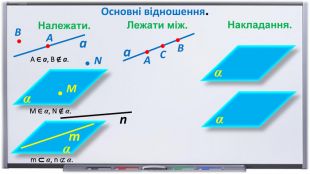
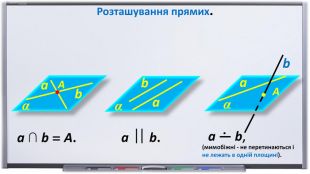
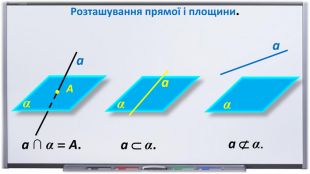
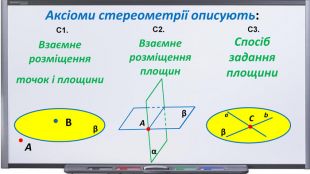
Презентація "Початкові відомості зі стереометрії" створена для учнів 9 класу, які вивчають геометрію в класах з поглибленим вивченням математики та може використовуватись також і для учнів 10 класу. У даному матеріалі використовується аксіоматика за Погорєловим О.В. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія (підручник для класів із поглибленим вивченням математики) 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку