Презентація "Поняття про теорію ймовірностей" 9 клас
Про матеріал
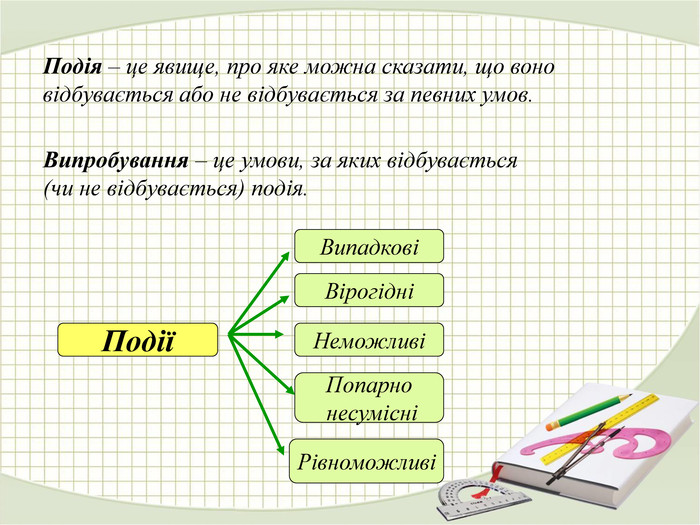
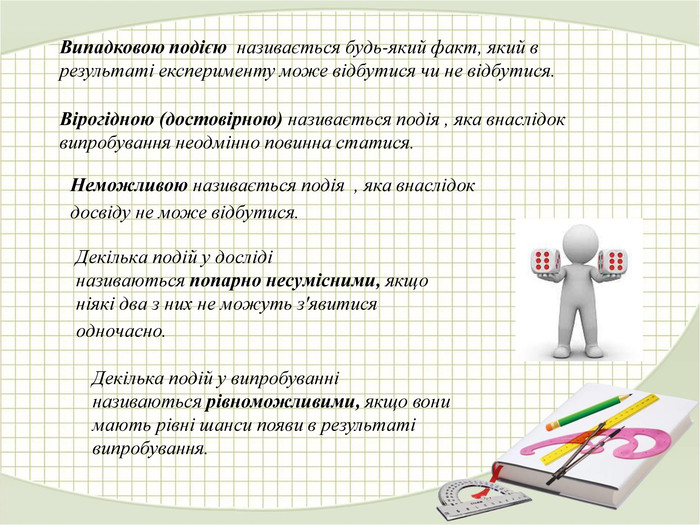
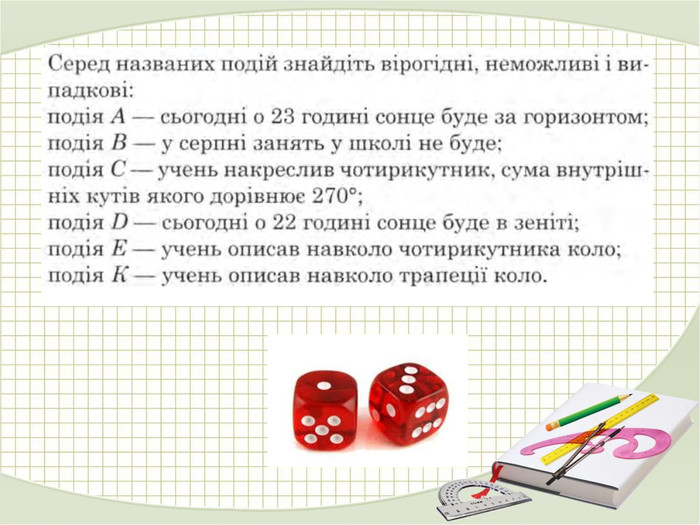
Матеріали презентації "Поняття про теорію ймовірностей" приведені у відповідність до підручника " Алгебра. 9 клас." (Г. П. Бевз, В. Г. Бевз) розділу 4 "Основи комбінаторики, теорії ймовірностей". Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку