Презентація "Просторові фігури. Початкові відомості про многогранники.Зображення фігур в стереометрії Задачі на побудову перерізів "
Про матеріал
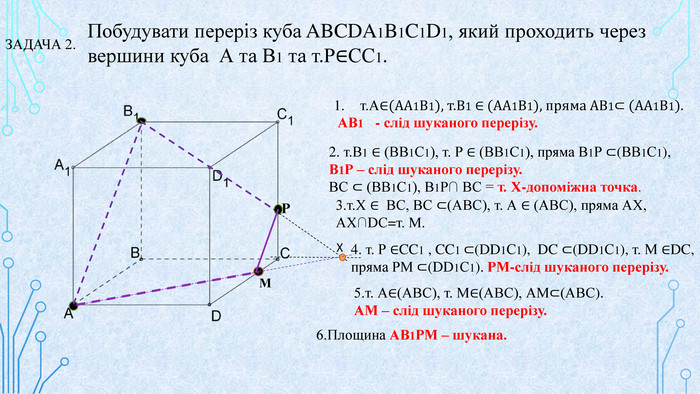
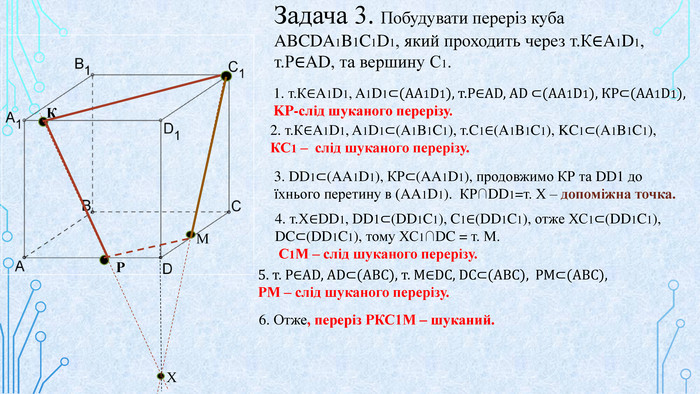
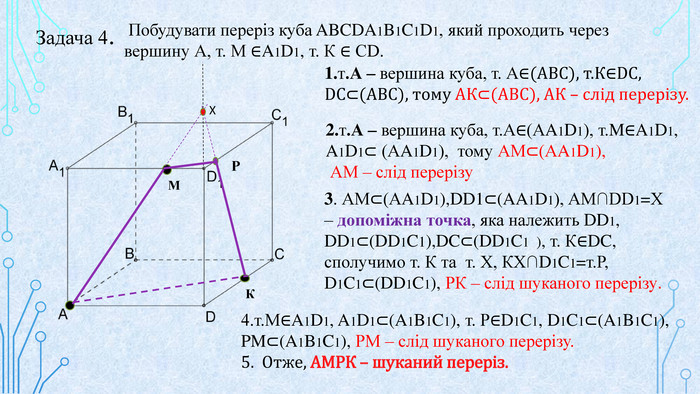
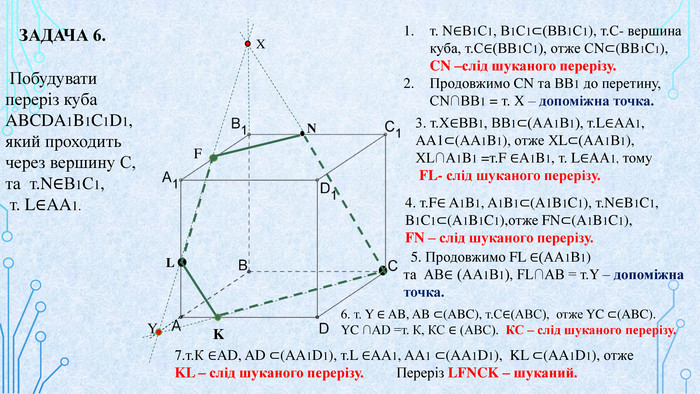
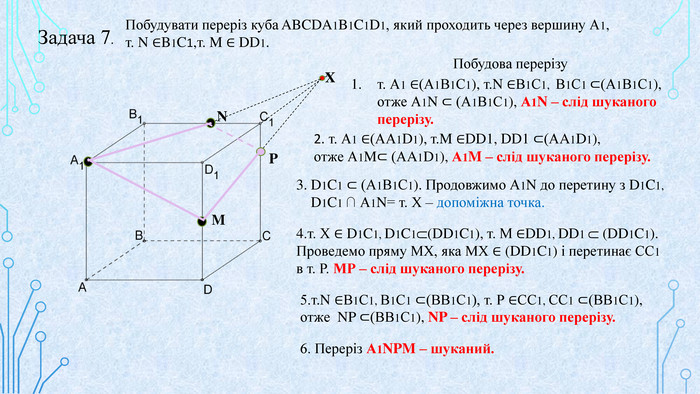
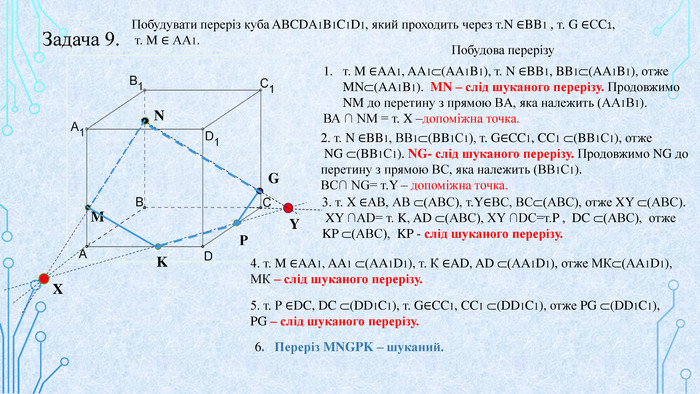
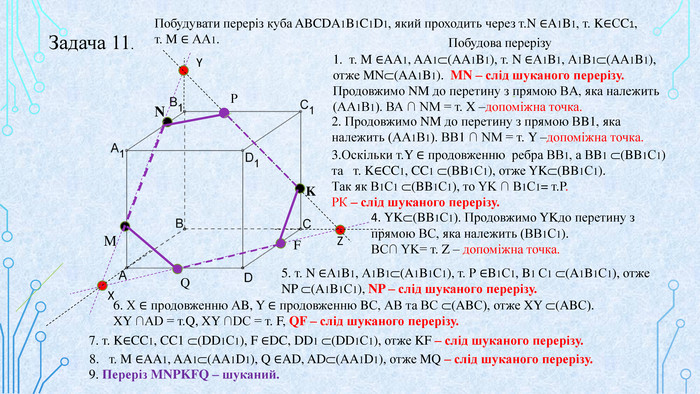
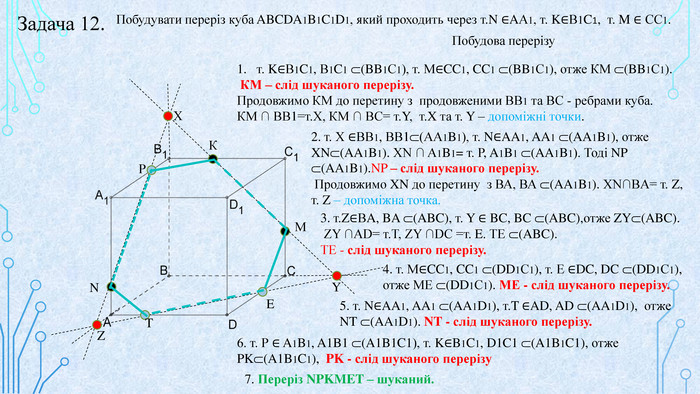
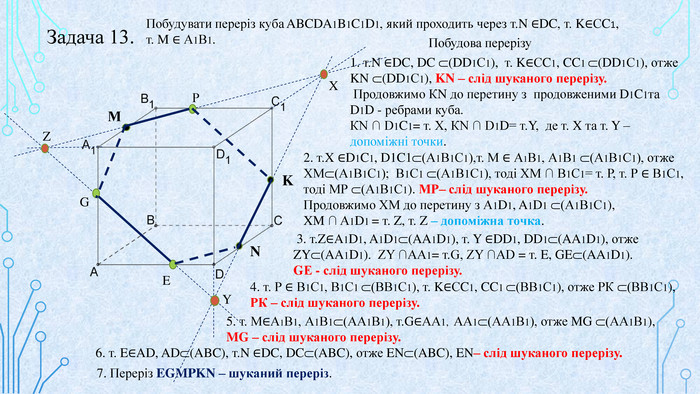
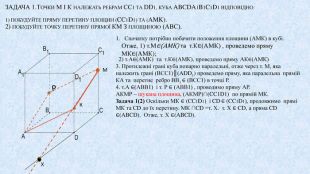
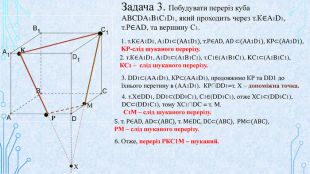
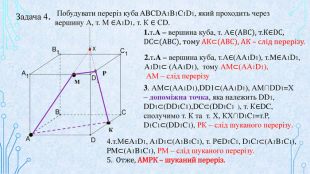
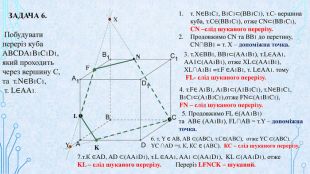
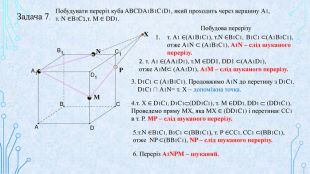
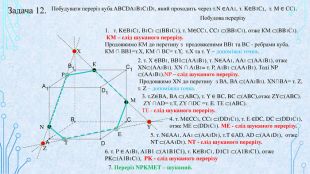
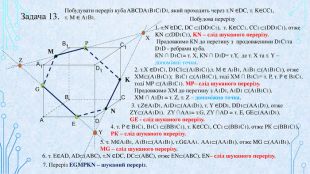
Матеріал призначений для використання на уроках геометрії в 10 кл. за програмою Стандарт, для поглибленого вивчення геометрії, навчання учнів побудови перерізів многогранників. В даній презентації використовується покрокове пояснення побудови перерізів в кубі. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку