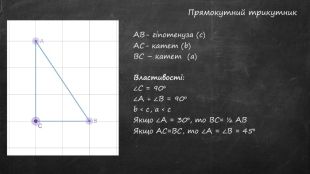
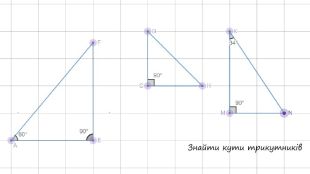
Презентація "Прямокутний трикутник"
Про матеріал
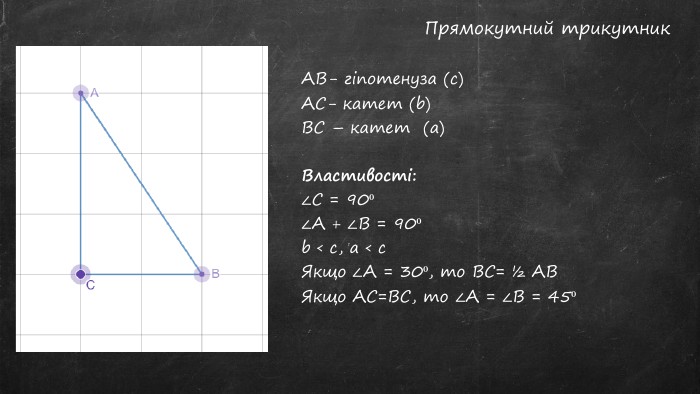
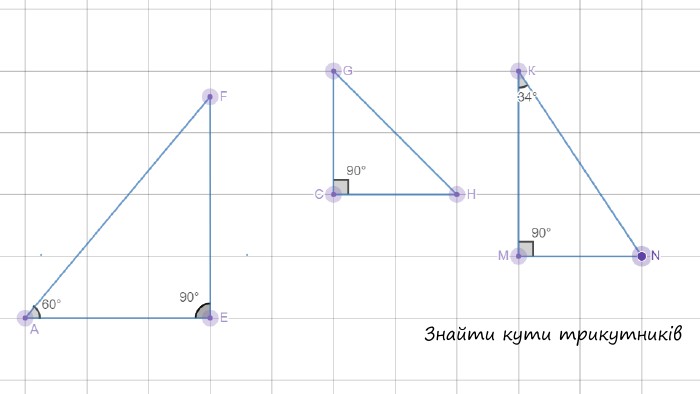
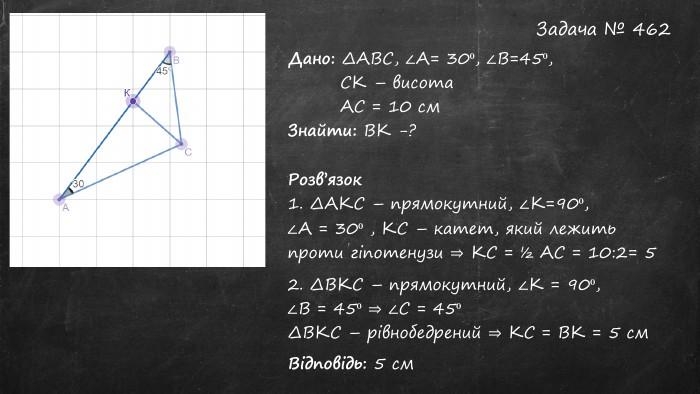
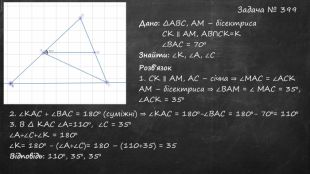
Презентація до уроку. Тема: Прямокутний трикутник. Починається з перевірки Д/З. Містить теоретичний матеріал та задачі, використовуються анімації. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
Чорний фон нічого не нагадує?


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку