Урок на тему " Свума кутів трикутника"

Тема уроку:  «Сума кутів трикутника»

 

Мета уроку:

1. Формувати поняття суми кутів трикутника, вміння знайти невідомий кут;  розширити  знання учнів про властивості трикутників.

2. Розвивати вміння виділяти головне в задачах, застосовувати набуті знання на практиці ,активізувати пізнавальну діяльність учнів, розвивати логічне мислення, математичну компетентність.

3. Виховувати самостійність, наполегливість у досягненні мети, цікавість до математики.

Тип уроку: засвоєння нових знань, умінь та навичок.

                                        Хід уроку.

Гасло : Найвищий прояв духу – це розум.

Найвищий прояв розуму – це геометрія .

Клітина геометрії - це трикутник.

Він такий же невичерпний як всесвіт.»

                                                                   Евклід.

 

І Вступ  Доброго дня діти! Сьогодні ми з вами починаємо вивчати нову тему, але вона буде пов’язана із вже відомою нам геометричною фігурою. Що це за фігура?

Навіть першокласник знає

Як трикутник виглядає

Має три він сторони

І кутів у нього три.

Відомий всім з дитинства трикутник приховує багато цікавого і загадкового, таємниці  якого ми й почали розкривати на уроках геометрії.

- Діти, скажіть мені, будь ласка, чого ви очікуєте від уроку? Які побажання, можете сказати один одному? (відповіді учнів)

Вправа на уважність .Скільки трикутників на малюнку. ( 13)

ІІ. Актуаліація опорних знань

Перш ніж опанувати нові знання треба пригадати «фундамент», який ми з вами заклали під час вивчення теми «Трикутник».

Яку фігуру називають трикутником?

Назвіть основні елементи трикутника?

Що таке периметр трикутника?

Як класифікують трикутники? Трикутники забули свої назви. Подивимось на малюнки і скажемо, які види трикутників ви бачите?

                        А                                                                           В

 

 

С

 

 

 

 

             В                         С            А                          В                 С                   А

 

Доповніть речення: (діти по черзі читають питання і доповнюють його).

1. Трикутник у якого дві сторони рівні є … .
2. Трикутник у якого всі сторони рівні є … .
3. Трикутник у якого є прямий кут називається … .

 

Гра «Встанови відповідність »

1 С   2 А    3 В     4 D

 ІІІ. Мотивація навчальної діяльності учнів

Завдання.  Побудувати трикутник за даними кутами

А = 90 ⁰                                   

В = 30 ⁰      

С = 90 ⁰                      

Запитання до класу:

Чи завжди можна побудувати трикутник за даними кутами?

 

Оголошення теми уроку : «Сума кутів трикутника».

 ІV. Засвоєння нових знань

Практичне завдання : Побудуйте трикутник.

1. Виміряти сторони трикутника
2. Вказати вид трикутника
3. Виміряти кути трикутника
4. Знайти суму кутів трикутника
5. ∟А+∟В + ∟С=180Зробити висновок

1.Теорема про суму кутів трикутника (з доведенням).

Теорема. Сума кутів трикутника дорівнює 180.

Дано: ∆ АВС

Довести: ∠А+∠В+∠С= 180

Доведення: Проведемо через вершину В пряму а∥АС. Утворені кути позначимо ∠1 та ∠2. Тоді ∠1= ∠С,а ∠2= ∠А. (як внутрішні різносторонні при а∥ AC і січних AВ і АС відповідно) кути 1, 2, В утворюють розгорнутий кут 180.

Наслідки з теореми.

Чи може трикутник мати два прямих кути?

 

V.

Усні вправи.

1 Чи існує  трикутник з кутами :

а) 6070;80

б) 20; 120 ;40 ( так)

в) 40; 80; 50 (ні)

г) 150; 10;20. ( так)

2. Знайдіть третій кут трикутника, та назвати його вид.

1) 20; 20;                     ( 120.) – тупокутний

2) 35; 55;                          (90 ) –прямокутний

3)60;80;                           (40) – гострокутний

Робота з підручником.

1. № 402.Кут при основі  рівнобедреного трикутника дорівнює 70⁰. Знайти кут при вершині.
2. Кут при вершині рівнобедреного трикутника в 2 рази  менший кута при основі. Знайдіть кути трикутника. (72 ; 36 ;72 )
3.  Трикутник з такими кутами називається  « Золотий трикутник». Існування поняття «Золотого трикутника»  не  тільки геометричне.

 Довідкова інформація.

Маркетингове правило золотого трикутника, як один із принципів мерчандайзингу. Використання золотого трикутника при розміщенні основного необхідного повсякденного товару, дає змогу на довше затримати покупців у магазині Вхід ⇒ Необхідна йому вітрина ⇒ Каса і є золотим трикутником. Чим далі одне від одного знаходяться “вершини” трикутника, тобто, чим більшу площу він охоплює, тим більше часу покупець проводить в торговому залі та тим більша кількість товарів попадає в поле його зору. Цим самим пояснюється, як і чому покупці купують більше, ніж запланували, навіть якщо “я всього на хвилинку” і “тільки за хлібом

 

 

Знайти висоту дерева, якщо з точки А, яка розміщена на відстані 5 м від основи дерева, його вершину видно під кутом 45˚.

 

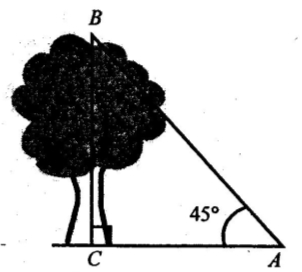
№ 406 (підручник )

414. У  трикутнику АВС <A:<B:<C= 3:4:5.Знайдіть ці кути.

 

VІ.  Підсумок  уроку:

 

Закінчіть речення:

Сума кутів трикутника дорівнює ….

Сума гострих кутів прямокутного трикутника дорівнює …

Прямокутний трикутник може мати  лише…

Тупокутний трикутник може мати лише…

 

VІІ. Домашнє завдання.

Параграф 17 № 396, 399,403.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Наслідок  з теореми про суму кутів трикутника

 

Чи може трикутник мати два прямих кути?

Чи може трикутник мати два тупих кути?  

Чи може трикутник мати прямий і тупий кути?

Висновок: Трикутник не може мати двох прямих або тупих кутів.

У кожному трикутнику принаймні два кути гострі (Наслідок із теореми про суму кутів трикутника)

 

Історична довідка.

Те,  що сума кутів трикутника дорівнює 180⁰ , було відомо в стародавньому Єгипті, проте доведено було значно пізніше. Вважають, що теорему про суму кутів трикутника довів Піфагор (VІ ст. до н. е.).