Презентація "Рівняння cos x = b"
Про матеріал
Презентація містить матеріал для вивчення даної теми на уроці алгебри 10 клас. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


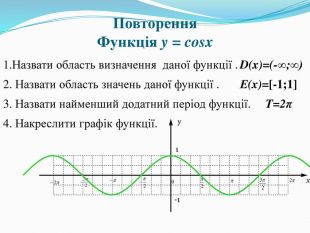
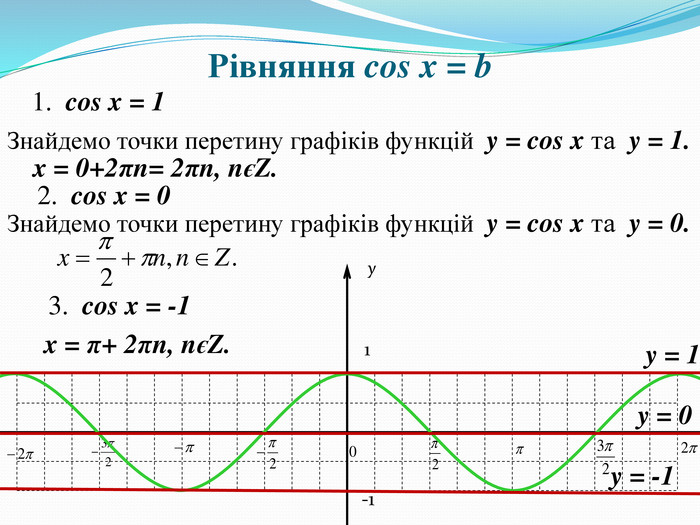
![Повторення. Функція y = cosx1. Назвати область визначення даної функції . D(x)=(-∞;∞)2. Назвати область значень даної функції . Е(x)=[-1;1]3. Назвати найменший додатний період функції. T=2π4. Накреслити графік функції.y1-1x Повторення. Функція y = cosx1. Назвати область визначення даної функції . D(x)=(-∞;∞)2. Назвати область значень даної функції . Е(x)=[-1;1]3. Назвати найменший додатний період функції. T=2π4. Накреслити графік функції.y1-1x](/uploads/files/20687/115150/125934_images/2.jpg)

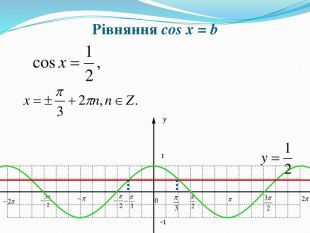
![Рівняння cos x = by1-1x. Корінь α має спеціальну назву – арккосинус. Означення. Арккосинусом числа b, де |b|≤1, називають таке число α, з проміжку[0;π], косинус якого дорівнює b. Рівняння cos x = by1-1x. Корінь α має спеціальну назву – арккосинус. Означення. Арккосинусом числа b, де |b|≤1, називають таке число α, з проміжку[0;π], косинус якого дорівнює b.](/uploads/files/20687/115150/125934_images/7.jpg)