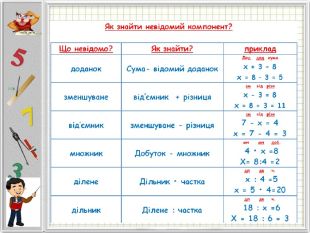
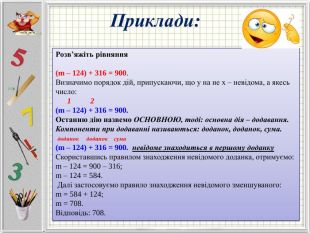
Презентація "Рівняння". Математика 5 клас за підручником Мерзляк.
Про матеріал
Презентація на тему "Рівняння" для 5 класу за підручником "Математика 5 клас" автори: Мерзляк, Полонський. НУШ. Перший урок. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку