Презентація "Розв'язування геометричних задач методом векторів."
Про матеріал
Матеріал для повторення та більш глибокого вивчення теми "Вектори у просторі"
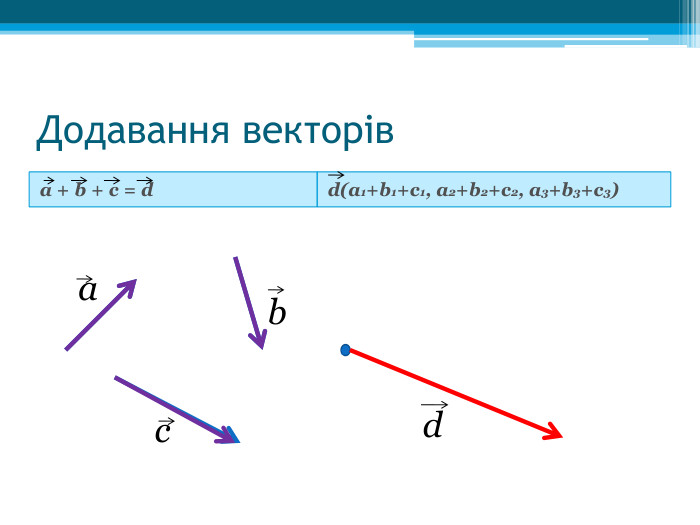
Суть методу векторів полягає в тому, щоб певне геометричне розміщення точок, прямих, площин у просторі
записати мовою векторів, точніше - у вигляді векторної рівності, і, навпаки, мову векторних формул і рівностей
наповнити геометричним змістом, тобто перевести ту чи іншу векторну рівність на мову геометрії, надати їй
геометричного звучання.
Особливістю методу векторів є те, що він не вимагає розгляду складних геометричних конфігурацій, а зводить
геометричну задачу до алгебраїчної, яку, звичайно, легше розв`язати, ніж вихідну геометричну.
Перегляд файлу
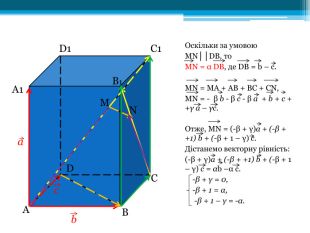
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку