Презентація: " Розв'язування показникових нерівностей з параметром"

Розв’яування показникових нерівностей з параметром

Перед людиною є три шляхи до пізнання: шлях мислення – найбільш благородний; шлях наслідування –найбільш легкий; шлях особистого дослідження – найбільш важкий. Конфуцій

Формування компетентностей:

1) предметна компетентність: удосконалити вміння розв’язування показникових нерівностей з параметром; 2) спілкування державною мовою: виховувати   культуру математичного мовлення;

3) математична компетентність: розвивати здібності учнів та креативний підхід до розв’язування нестандартних задач та проблем, формувати ціннісні орієнтації ; 4) уміння вчитися впродовж життя – уміння використовувати знання в новій ситуації.

При    розв’язуванні  задач з параметрами    потрібно пам’ятати наступне:

-            при різних значеннях параметра задача може розв’язуватись по-

різному;

-            при розв’язуванні нерівностей з параметром хід розв’язку може

залежати від взаємного розміщення коренів відповідного рівняння;

-            графічний метод (тобто аналіз властивостей функцій за допомогою зображення їх графіків при різних значеннях параметра) дозволяє полегшити аналітичні викладки.

Приклад 1. За яких значень параметра а нерівність 4^х-а − 42^х + 4 > 0 виконується для будь-яких дійсних значень х? У відповідь записати найбільше ціле значення а.

Розв’язання. Нехай 2^х =t, t> 0. Одержимо квадратну нерівність 𝑡² -(a-4)t+4> 0. Тоді завданя полягає: визначити за яких значень параметра а графік функції f(t) =𝑡² -(a-4)t+4 на проміжку (0; +∞) розміщений над віссю t? Це можливо у двох випадках.

1) Графік функції y=f(t) міститься над віссю t для будь-якого t, а отже, і на інтервалі (0; t), якщо дискримінант квадратного тричлена f (t) від’ємний, тобто (а-4)²-16< 0; а²-8а+16-16< 0; а(а-8) < 0. Графіком даної квадратичної функції є парабола, вітки якої напрямлені вгору і нулями є 0 та 8. А тому розв’язок останньої нерівності: а∈(0; 8). 2) Якщо D≥ 0, то тричлен f(t) не повинен мати додатних коренів. А це можливо за умови:

                        f(0) ,                       4>0,

0,  звідки        а<4,                             а ∈ (-∞;0]. Об’єднавши розв’язки 1) і 2)

D≥  0;                            а ∈ (-∞;0] U[8; ∞);      одержимо а ∈ (-∞;8]. Найбільше ціле значення а=7.

Відповідь: 7.

Приклад 2. Знайдіть всі значення параметра а при яких  нерівність 4^х-а 2^х-а+3≤ 0 має хоча б один розв’язок.

Розв’язання. Дану нерівність можна переписати у вигляді  а, яка рівносильна  нерівності а .

Зрозуміло, що якщо а ≥ min f(x), то початкова нерівність має хоча б один розв’язок. Введемо заміну 2^х =t, дослідимо  на найбільше та найменше значення функцію ^{g(t) =𝑡2+3} з областю визначення D(g) = (0;∞). Маємо

𝑡+1

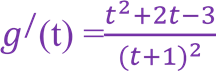 . Враховуючи, що t >0, одержимо, що 𝑔^/(t)=0, якщо t=1.

Якщо 0 < t < 1, то 𝑔^/(t) < 0. Якщо t > 1, то 𝑔^/(t) > 0. Звідси на проміжку (0; ∞) min g(t)= g(1) =2, a min f(x)=f(0)=2 на проміжку (-∞; ∞). Таким чином, початкова нерівність має хоча б один розв’язок, якщо а ≥ 2. Відповідь: а 𝜖 [2; ∞).

Домашнє завдання. Для кожного значення параметра а розв’яжіть нерівність (х-а) 3 ∙ 2^х − 2 ∙ 3^х ≥ 0.

Бажаю успіху!