Презентація "Розв'язування задач на відсотки за допомогою систем лінійних рівнянь з двома змінними"
Про матеріал
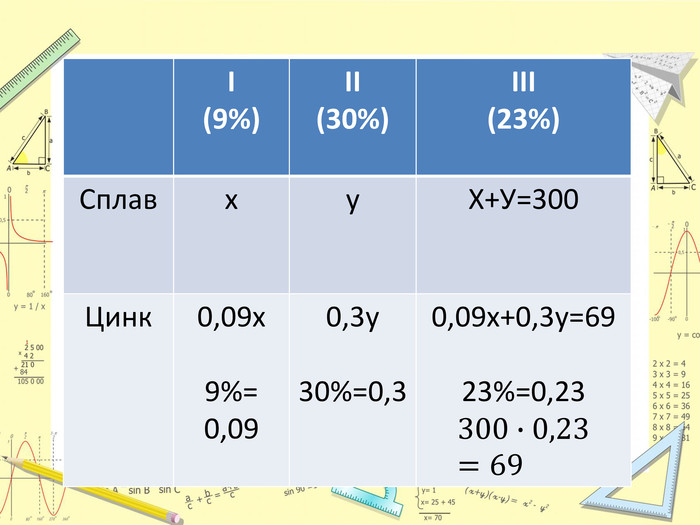
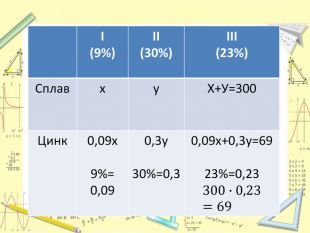
Дана розробка містить задачі на відсотки, задачі на суміші та сплави, задачі на знаходження двозначного числа. Можна використовувати на уроках та під час дистанційного навчання. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Розв'язування задач за допомогою систем лінійних рівнянь Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку