Застосування формул скороченого множення

Тема уроку:  ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ

Мета уроку:    

                          – навчальна формувати, удосконалити та поглибити знання та вміння учнів використовувати формули скороченого множення при розв'язуванні вправ, формувати навички їх творчого застосування при розв'язуванні завдань високого рівня складності;

• розвивальна

розвивати логічне мислення, математичну мову, вміння чітко висловлювати думки, узагальнювати, активність;

• виховна
• виховувати пізнавальну діяльність учнів, активність, уважність, самостійність, інтерес до математики.

 

Очікувані результати:

учні повинні знати формули скороченого множення, вміти застосовувати формули до обчислення значень виразів, розв’язування рівнянь.

 

Тип уроку: урок застосування знань умінь навичок.

Обладнання: роздатковий матеріал, картки з відповідями, картки самоконтролю. Форми роботи: колективна, індивідуальна.

 

ХІД УРОКУ

 

Девіз уроку: «Найкращий спосіб вивчити що-небудь – це відкрити самому»                (Д . Пойа, угорський, швейцарський, американський математик)

 

І. ОРГАНІЗАЦІЙНА ЧАСТИНА

 

ІІ. ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ

Вже від початку навчального року ми з вами подорожуємо містами нової для вас країни Алгебри. Нещодавно ми дісталися ще одного міста – ФСМ, що означає Формули скороченого множення.

Сьогодні ми пройдемося вулицями цього міста, щоб дізнатися, що тут є цікавого і незвичайного.

Працювати ми будемо над темою «Повторення та застосування формул скороченого множення».

 У кожного з вас на парті лежать картки самооцінювання. Сьогодні ми будемо працювати на довірі. Оцінювати себе ви будете самі.

Мотивація навчальної діяльності учнів.

Сьогодні на уроці ми підіб’ємо підсумки вивчення теми «Формули скороченого множення», будемо продовжувати виробляти навички застосування формул скороченого множення при тотожних перетвореннях многочленів.

Отже, наскільки ви компетентні у застосуванні формул скороченого множення при тотожних перетвореннях многочленів, покаже сьогоднішній урок.

 

ІІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

Для  подорожі містом, нам слід бути впевненими, настільки добре  ми до неї підготувались.

Звірте з дошкою правильність розв’язання домашнього завдання та оцініть його.

    1) (х+3)²=х²+6х+9;   

    2) (a²-c)²=a⁴-2a²c+c²;    

    3) (ax+b²)²=a²x²+2axb²+b⁴;      

    4) (-1+2c³)²=4c⁶-4c³+1;    

    5)   12ab-(2a+3b)²=12ab-4a²-12ab-9b²= -4a²-9b²;    

    6)  (х-3)² =(х-5)(х+4);                          

         х²-6х+9=х²+4х-5х-20;                        

        -6х-4х+5х= -20-9;                               

        -5х= -29;                                             

              х= 5,8.  

                                              

ІV. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Щоб зайти в місто я повинна бути впевнена, що ви бадьорі і сповнені сил

• Графічний тренінг

Якщо вираз записано правильно, то учні ставлять в зошиті ˄, а якщо не правильно, то _

Вправа «Знайди помилку»

1. (b-y)²=b²-2by+y²
2. (3a+5b)²=9a²+30ab+25b²
3. (3п-2р)²=3п²-12пр+2р²
4. (2a+1)²=4a²+4a+1
5. 49-c²=(49-c)(49+c)
6. (p-10)²=p²-20p+100
7. (2а-с)(2а+с)=4а²-с²

 (Правильний запис ˄˄_˄_ ˄˄)

На що схожі ваші записи? На кардіограму. Отже, ваша кардіограма вказує на те, що настрій у вас гарний і ви готові відвідати наше місто ФСМ.

 

Але для успішної подорожі містом нам потрібно придбати перепустки, які ви отримали на попередніх уроках.

Давайте разом пригадаємо з вами основні формули скороченого множення

- квадрат суми двох виразів

- квадрат різниці двох виразів

a²-b²=(a-b)a+b)- різниця квадратів двох виразів

 

• Гра «Дивись, не помились!».

На дошці записані завдання. Потрібно відновити записи – вставити пропущені символи.

 

Завдання. Відновіть записи:

1. (a+b)²=a²+2ab+…
2. (m-…)²=m²-2mn+n²
3. (…+y)²=…+2xy+y²
4. (a²…b)²=…-2a²b+b²
5. (3-y)²=9…6y…y²
6. (3x+2y)(3x-…)=9x²-4y²
7. (6x-…)²=36x²-…+1

 

 

- Конкурс-розминка «Мозковий штурм»

1. Укажіть за допомогою сигнальних карток номер правильної відповіді. Якщо правильної відповіді немає, то укажіть її.

Завдання	Вибери відповідь	Відповідь
1. ;	1. ;	4-1
2. ;	2. ;	2-5
3. ;	3. ;	3-2
4. ;	4. ;	4-1
5. ;	5. .	5-3

 

2. Закінчить вирази: Відповідь:

1) ;    ;

2) ;    ;

3) ;      ;

4);     ;

5);    .

 

3.Обчисліть:Відповідь:

1);    ;

2);   .

4. Знайдіть суму коренів рівняння .

Відповідь: 1.

5. Заповніть порожні клітинки: Відповідь:

1) (+6b)(-)=25a²-;

;

2) (3с-)²=-+25;.

 

Отже, сьогодні ми будемо працювати над повторенням формул скороченого множення, і дізнаємось, де їх можна використовувати.

 

V. ІСТОРИЧНА ДОВІДКА

Ось ми уже в місті ФСМ. І одразу ж потрапили на станцію «Історичну». Розгляньте уважно рисунок.

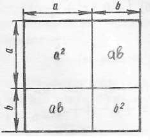          Формули скороченого множення, які ми зараз вивчаємо, античні математики використовували задовго до нашої ери. На той час формули подавалися не у звичному нам символічному вигляді, а формулювалися словами.

 Учені Давньої Греції алгебраїчні твердження, формули, що виражають певні залежності між величинами, трактували геометрично. Так, добуток вони розглядали як площу прямокутника зі сторонами та .

 Подивимося з вами на приклад алгебраїчного твердження, яке було відомим давньогрецьким ученим, і яке в геометричній термінології формулювалося так:

Площа квадрата, побудованого на сумі двох відрізків, дорівнює сумі площ квадратів, побудованих на кожному з цих відрізків, плюс подвоєна площа прямокутника, побудованого на цих відрізках. Як ви вважаєте, про яку формулу скорочено множення йдеться мова?

 Мова йдеться про формулу квадрата суми, яку ми символічно записуємо так:

.

Давньогрецький учений Евклід (3 ст. до н. е.), який створив посібник з математики «Начала», першим геометрично вивів формулу квадрата двочлена (буквенна символіка була введена пізніше у XVI-XVII ст.)

 

VІ.  ФІЗКУЛЬТХВИЛИНКА

Не можна пройти повз   вулиці «Спортивної». Погляньте як тут цікаво!  Давайте і ми з вами приєднаємося до жителів цієї вулиці.

 

     VІІ. РОЗВ’ЯЗУВАННЯ ВПРАВ НА ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ

Продовжуємо свою подорож. І ось вулиця «Рахувати-Хитрувати». Завітаємо сюди.

• Застосування формул скороченого множення для виконання обчислень (швидкої лічби).

1.   За допомогою якої формули  скороченого множення легко обчислити значення

 99·101

 99·101= (100-1)(100+1)=100² - 1=9999

 

Показати учням кілька прикладів знаходження квадратів двоцифрових чисел, що закінчуються цифрою 5.

Наприклад, 25²=625; 35²=1225; 75²=5625 і. т. д.

 

2. Обчислити: 57·53.

Розв’язання:

Приклад 2. Знайти 99².

Розв'язок. Застосуємо формулу для різниці в квадраті

Як можна переконатися з обчислень - це легше, ніж часом знайти в потрібний момент калькулятор.

 

Приклад 3. Піднести до квадрату вираз
(x+y-3).

Розв'язок. Суму перших двох доданків уявно вважаємо одним доданком і за другою формулою скороченого множення знаходимо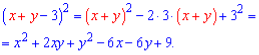

В такий спосіб отримали вадратичну залежність для двох змінних.

 

Приклад 4. Знайти різницю квадратів
11²-9².

Розв'язок. Оскільки числа невеликі то можна просто підставити значення квадратів

Але мета в нас зовсім інша – навчитися використовувати формули скороченого множення для спрощення обчислень. Для цього прикладу застосуємо третю формулу

При великих числах і невеликою різницею між ними така схема набагато ефективніша ніж підносити до квадратів, а пізніше шукати різницю квадратів.

 

Приклад 5. Знайти різницю квадратів
17²-3².

Розв'язок. На цьому прикладі Ви вже захочете вивчити правила, щоб обчислення звести до одного рядка
 

Приклад 6. Спростити вираз
(x-y)²-(x+y)².

Розв'язок. Можна розкладати квадрати, а пізніше сумувати подібні доданки. Проте можна прямо застосувати різницю квадратів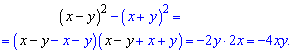
 

 

 

• Застосування формул скороченого множення для піднесення довільного многочлена до квадрата.

Наша подорож триває. Ми дістались вулиці «Дослідників». Давайте заглянемо, що тут відбувається.

Перейдемо до одного узагальнення, початок якому поклали стародавні вавілоняни.

 Ви знаєте тотожність (a+b)²=a²+2ab+b².

Запропонуйте спосіб піднесення двочлена до кубу.  (a+b)³=(a+b)²(a+b)=(a²+2ab+b²)(a+b)=a³+a²b+2a²b+ab²+b³=

=a³+3a²b+3ab²+b³.

Що ви можете сказати за показники числа а? (спадають); числа b? (зростають).

А якщо піднесемо двочлен до четвертого степеня, які будуть показники степенів? (Розписати без коефіцієнтів:

(a+b)⁴=   a⁴+  a³b+   a²b²+   ab³+   b⁴

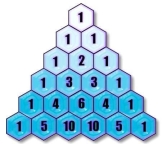
 Чого не вистачає в цій формулі? (Коефіцієнтів.) Спробуємо знайти їх за допомогою незвичайного трикутника.

 Можна побачити, що “сторони” цього трикутника складені із одиниць, а числам, які стоять всередині трикутника, притаманна властивість. Яка? (Кожне число можна подати у вигляді суми чисел, які стоять над ним у попередньому ряду праворуч і ліворуч:

Спробуйте дописати наступні рядки і виправити формулу четвертого степеня двочлена:

(a+b)⁴ =a⁴+4a³b+6a²b²+4ab³+b⁴.

 Піднесіть двочлен до п’ятого степеня, використовуючи вказані властивості: 

(a+b)⁵ =a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵.

 Трикутник, складений за вказаним правилом, називають трикутником Паскаля, названим ім’ям відомого математика, фізика, філософа, письменника Блеза Паскаля (1623 - 1662), сучасника Декарта і Ферма.

 Де ви чули це прізвище?

• На уроках фізики: тиск вимірюється в паскалях.
• На уроках інформатики: існує мова програмування Паскаль.

 Отже, яким чином ми узагальнили формулу квадрата двочлена?

(Навчились підносити двочлен до будь-якого натурального степеня)

 

• Застосування формул скороченого множення для спрощення і перетворення виразів.

Продовжуємо свою подорож. І ось ми дісталися «Вулиці письменників». Які цікавинки нас чекають тут?

Математичне лото

Відповіді знаходяться на зворотному боці карток, де записані завдання. При правильному виконанні учні мають отримати  вислів М. Горького: «Немає сили могутнішої за знання; людина, озброєна знаннями, - непереможна».

Спростіть вираз:

Робота в парах:

1. (5х-3)(5х+3)-25х²
2. (а-5)²-а(а-10)
3. (х+4)²+(х+1)(х-9)
4. (х-1)²-(х-2)²
5. (3х+2)²+(3х-2)²
6. (х-2)²-(х-3)(х+3)

 

 

Картки із диференційованими завданнями;

 

Рівень А

 

Виконайте за зразком:

Відповідь:

1. ;

2. ;    ;

3. ;    ;

4. ;    ;

5. ;

6. ;     ;

7. ;     .

 

 

Рівень Б

Обчисліть:Відповідь:

1. ;  ;

2. Спростіть ;  9;

Розв’язання: .

3. (+7)( -7)=с²-²;(с+7)(с-7)=с²-7²=с²-49.

 

Рівень В

 

1. Доведіть, що вираз ділиться на 7.

Доведення. ділиться на 7, отже ділиться на 7.

2. Спростіть вираз Відповідь:

..

 

 

 

• Застосування формул скороченого множення для розв’язування рівнянь.

І наша подорож закінчується відвідуванням будинку, де проживає «Містер Х»

1. 2х(8х-5)-(4х+1)²=35 – з поясненням біля дошки
2. х(х-2)-(х+5)²=-1 – самостійно.

 

КВИТОК ДОДОМУ.  Знайдіть у правій колонці відповіді до прикладів у лівій колонці.

1.                                                                       1.

2.                                                               2.

3.                                                                  3.

4.                                                                       4.

5.                                                                    5.

6.                                                             6.

 

Правильні відповіді
        1 - 5
        2 - 6
        3 - 1
        4 - 3
        5 - 2
        6 - 4

 

VІІІ. ПІДСУМКИ УРОКУ

 

Наш урок закінчується. Згадайте, які слова частіше зустрічалися на уроці: «знаю», чи «вмію»?

Підсумок уроку.

Рефлексія
Учитель:
Ян Амос Коменський сказав: «Вважай нещасним той день і годину, в який ти не засвоїв нічого нового і не додав до своїх знань»
1) Що ви додали в свої знання сьогодні на уроці?
2) Які завдання були найскладнішими?
3) У чому причина помилок, яких припустилися під час розв’язування вправ?
4) Які завдання виявилися легкими?
5) Що найбільше сподобалося на уроці?

 

ДОМАШНЄ ЗАВДАННЯ.№705, тестові завдання №4.с.113(підручник" Алгебра " авт. Мерзляк А.Г., Полонський В.Б., Якір М.С.)

гр.Б завдання 7, 10, сторінка 149.

 

• Учні ставлять собі оцінку за урок і здають картки самооцінювання.
• Вчитель дякує за урок.

Я сподіваюсь, що вам сподобалася подорож містом ФСМ і ви відкрили для себе щось нове і цікаве; ви переконалися, що знання формул є досить важливим, оскільки набагато скорочує нашу роботу, а також допомагає при розв’язуванні нестандартних завдань і навіть завдань олімпіадного типу. І цим самим наші сили після цього уроку зміцніли. Тож, я бажаю вам набиратися сил з великою швидкістю, щоб у майбутньому стати непереможними!