Презентація "Синус, косинус, тангенс гострого кута прямокутного трикутника"
Про матеріал
Презентація містить повний теоретичний матеріал до уроку "Синус, косинус, тангенс гострого кута прямокутного трикутника. Також подані завдання практичної роботи та вправи на усне опрацювання.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



























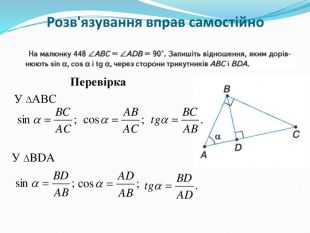



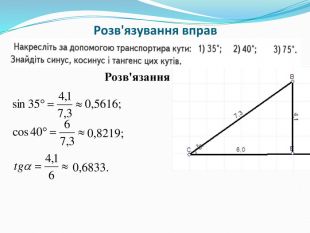
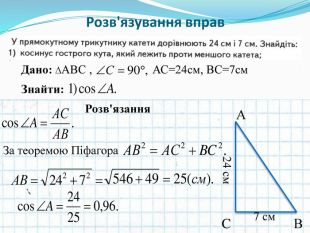
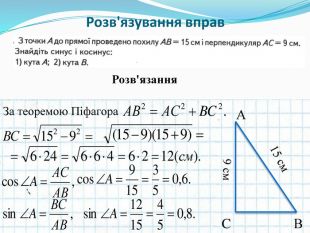

-

Мирошниченко Зоя Михайлівна
28.01.2025 в 09:51
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
17.03.2024 в 23:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шилик Яна Олександрівна
03.03.2024 в 11:19
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Мірінська Тетяна
06.03.2023 в 21:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
02.02.2023 в 16:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
14.02.2022 в 22:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Модягина Наталія
15.04.2021 в 08:08
СУПЕР
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Полинюк Тамара Михайлівна
02.02.2021 в 22:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
02.12.2020 в 20:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Назаратій Світлана Василівна
08.04.2020 в 10:52
Дякую колезі за гарну роботу!
Чітко, влучно, виважено. Найважливіші слайди навіть помічено.
Планую використати для актуалізації знань перед вивченням теми "Тригонометричні функції" у старшій школі.
Дякую! Наснаги та успіхів!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мисік Марина Олександрівна
10.04.2019 в 08:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 8 відгуків