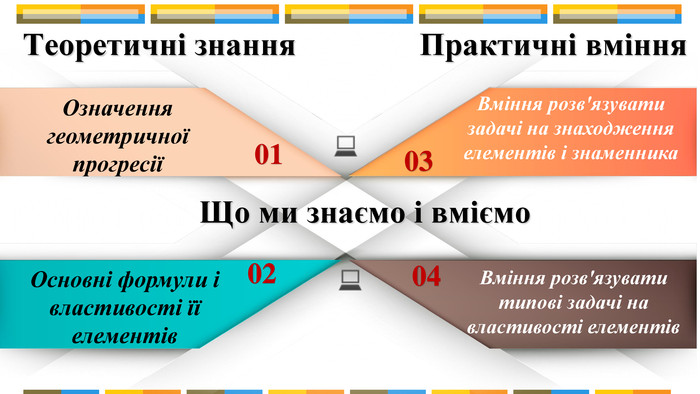
Презентація :"Сума геометричної прогресії"

Алгебра 9 клас

Геометрична прогресія2 Формула суми геометричної прогресіїАлгебра 9

0102 Означення геометричної прогресії0304 Теоретичні знання. Основні формули і властивості її елементів. Практичні вміння. Вміння розв'язувати задачі на знаходження елементів і знаменника. Вміння розв'язувати типові задачі на властивості елементів Що ми знаємо і вміємо

Яка послідовність є геометричною прогресією?1234

Знайти знаменник прогресії123420,14-2

4 Введемо формулу суми n перших елементів геометричної прогресії.123 Сьогодні на уроці : Розглянемо прикладні задачі на прогресіїРозв'яжемо типові задачіРозглянемо легенду про шахи

У Стародавній Греції в часи Евкліда і Архімеда (ІІІ ст. до н. е.) властивості прогресій розглядались у зв’язку з теоретичними дослідженнями. Так, у книзі Евкліда “Начала” доводиться властивість трьох послідовних членів геометричної прогресії.

Історична задача. Задача із папірусу Рінда “Є 7 будинків, в кожному будинку по 7 котів, кожен кіт з’їдає 7 мишей, кожна миша з’їдає по 7 колосків ячменю, кожен колосок, якщо посіяти зерно з нього, дає 7 мір ячменю. Знайти суму загального числа будинків, котів, мишей, колосків і мір”. Ця стародавня задача на геометричну прогресію не раз зустрічається в різних народів з дещо зміненим текстом.

Умова математичною мовою: Дано: геометрична прогресія 𝑏𝑛:𝑏1=7;q=7. Знайти :𝑆5. 

Розв'язання: Знайдемо всі необхідні елементи: 𝑏2=𝑏1∙𝑞=7∙7=49; 𝑏3=𝑏2∙𝑞=49∙7=343; 𝑏4=𝑏3∙𝑞=343∙7=2401; 𝑏5=𝑏3∙𝑞=2401∙7=16807. 𝑆5=7+49+343+2401+16807=19607. 

Виникає питання: Чи обов'язкове визначати всі елементи прогресії, суму яких треба знайти ?Чи є формула, яка дозволяє виконати це раціональним способом?24.03.202011

Формула суми n перших елементів .24.03.202012

Умова математичною мовою: Дано: геометрична прогресія 𝑏𝑛:𝑏1=7;q=7. Знайти :𝑆5. 

Розв'язання: Знайдемо  шукану суму за відповідною формулою: 

Типові задачі на визначення суму геометричної прогресіїРозвиваємо практичне вміння розв'язування задач .

24.03.202016№1

Прикладні задачі на геометричну прогресію. Математика безумовно має прикладне значення. Яку б тему ми не вивчали, існують задачі економічного, екологічного, хімічного, фізичного змісту, які розв'язуються за допомогою математичного апарату.

В посудині є 50 л 80% спирту. Скільки літрів чистого спирту буде в посудині, якщо з неї відливати 20 раз по 1 л рідини і щоразу доливати по 1 л чистої води (відповідь округлити до десятих частин)?№1 Розв’язання: Знайдемо початкову кількість спирту: 50⋅0,8=40(л). Концентрація спирту у розчині постійно зменшується за правилом спадної геометричної прогресії.

24.03.202019 Нехай прогресія (сn ), тоді її перший член с1 =0,8, а останній с21 ( так як 20 раз проводився певний цикл переливання). Об’єм рідини постійний (50 л),бо доливали і відливали одну й ту саму кількість літрів ( 1 л ). Кількість спирту наприкінці циклу 50⋅ с21 ,А за крок до цього ця ж сама кількість спирту (50-1)⋅ с20 , тоді 50⋅ с21 = (50-1)⋅ с20 .

Так як знаменник прогресії 𝒒=𝒄𝟐𝟏𝒄𝟐𝟎,  тоді  q=𝟒𝟗𝟓𝟎=𝟎,𝟗𝟖. За формулою геометричної прогресії: с21 =с𝟏∙𝒒𝟐𝟎=0,8⋅𝟎,𝟗𝟖𝟐𝟎  . Кількість спирту: 𝟓𝟎⋅𝟎,𝟖⋅𝟎,𝟗𝟖𝟐𝟎  ≈𝟐𝟔,𝟕л. Відповідь: 26,7 л.  

Доведено, щопри підвищенні температури у арифметичній прогресії швидкість деяких хімічних реакцій зростає у геометричній прогресії.24.03.202021

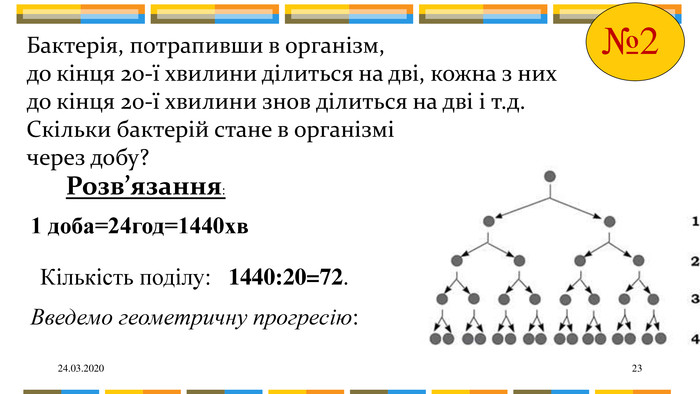
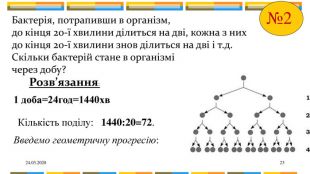
Біологія. Відомо , що бактерії розмножуються за законом: одна бактерія ділиться на дві. Саме тому їх кількість швидко зростає, якщо їх помістити в сприятливе середовище. В повсякденному житті, коли хочуть підкреслити швидке зростання якоїсь величини, кажуть: “зростає в геометричній прогресії ”.

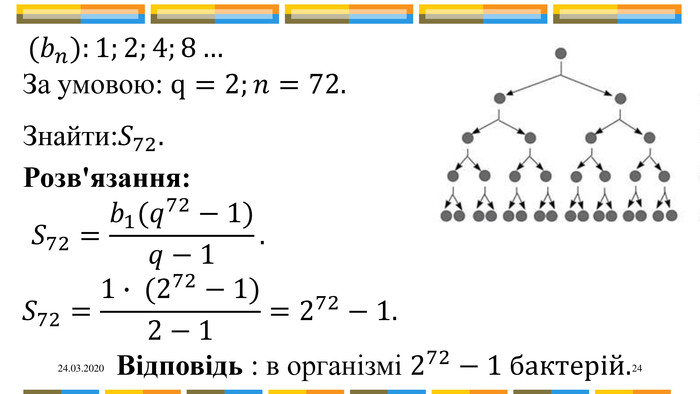
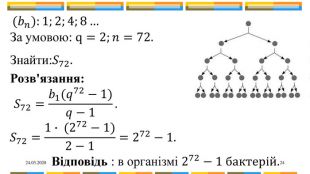
24.03.202023 Бактерія, потрапивши в організм, до кінця 20-ї хвилини ділиться на дві, кожна з них до кінця 20-ї хвилини знов ділиться на дві і т.д. Скільки бактерій стане в організмі через добу?№2 Розв’язання:1 доба=24год=1440хв Введемо геометричну прогресію: Кількість поділу: 1440:20=72.

24.03.202024(𝑏𝑛):1;2;4;8… За умовою: q=2;𝑛=72. Знайти:𝑆72. Розв'язання:𝑆72=𝑏1(𝑞72−1)𝑞−1. 𝑆72=1∙ (272−1)2−1=272−1. Відповідь : в організмі 272−1 бактерій. 

Інтенсивність розмноження бактерій використовується в…в харчової промисловості для виготовлення кисломолочних Продуктівпри квашении, заквасці та засолці.в фармацевтичній промисловості (для створення ліків та вакцин)в сільському господарстві: для Виготовлення силосу кормів для тварин

Задача-легендаІндійському царю Шераму дуже сподобалась гра у шахи. Він вирішив нагородити свого підданого Сету за винахід такої чудової гри . І запропонував вибрати нагороду винахідцу самостійно. На це Сета відповів, що йому нічого казкового не треба, але попросив видати зерна пшениці за такою умовою:на першу шахову клітинку покласти 1 зерно, на другу — 2 зерна, на третю — 4 зерна і т. д. Царь, посміхаючись над Сетой , наказав видати йому таку «скромну» нагороду. style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Задача-легенда. Але наступного дня, коли Сета з'явився за винагородою, виявилось, що виконати таке просте, на перший погляд, прохання винахідника неможливо. Причина : такої кількості зерен немає і бути не може. Виходить, Шерам посміхався дарма. Ця задача належить до початку нашої ери. А тепер розв'яжемо її :style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Дано: геометрична прогресіяb1 = 1, q = 2, n = 64. S64 - ?Розв'язання: Багатий раджа був приголомшений, коли дізнався, що він не в змозі задовольнити це “скромне” бажання. Для того, щоб зрозуміти, наскільки величезним є це число, уявимо, що зерно зберігають у коморі площею 12 га, висота якої була б більшою за відстань від Землі до Сонця.

Творче завдання:24.03.202029 Знайдіть приклади практичного використання арифметичної , геометричної прогресії в нашому житті.

Дякую за увагу24.03.202030

24.03.202031