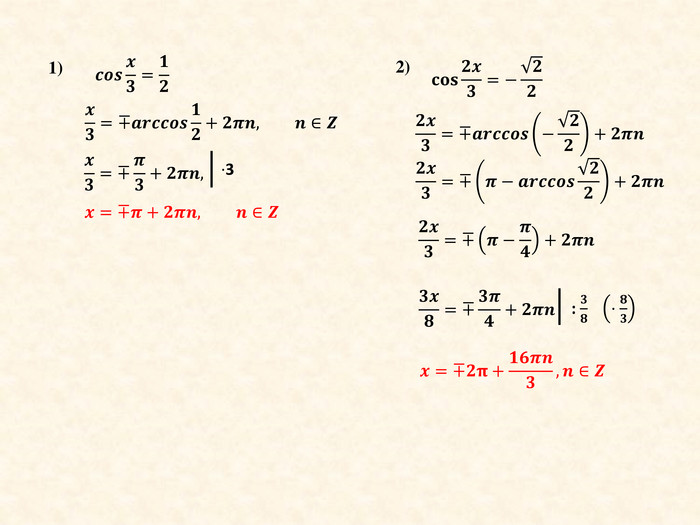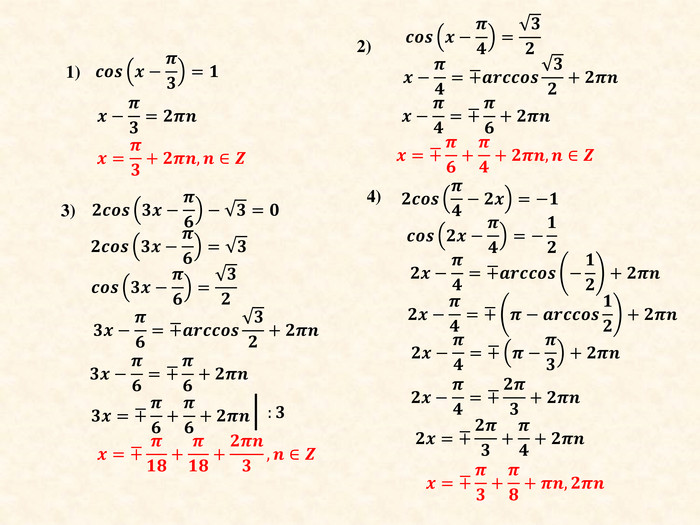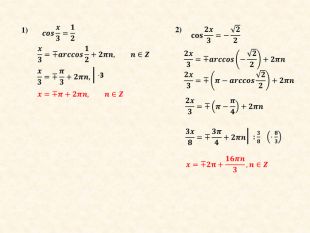Презентація до уроку "Розв'язування тригонометричних рівнянь y=cosx" (ІІ частина)
Про матеріал
Продовження розв'язування більш складних тригонометричних рівнянь y=cosx. Матеріал створювався для проведення онлайн-уроків під час карантину
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку