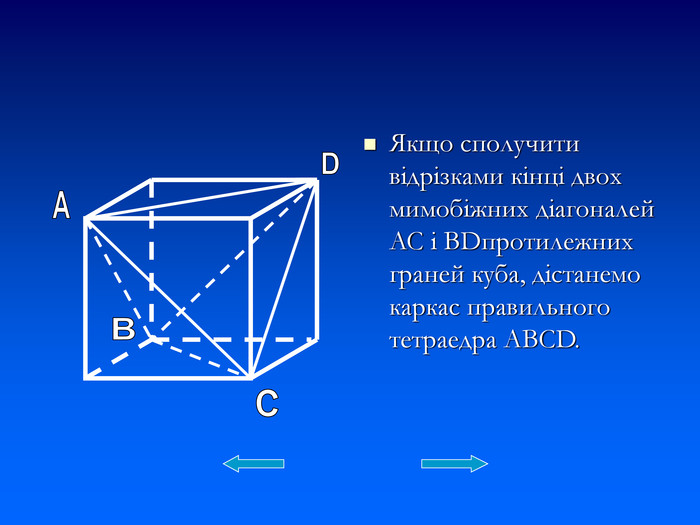
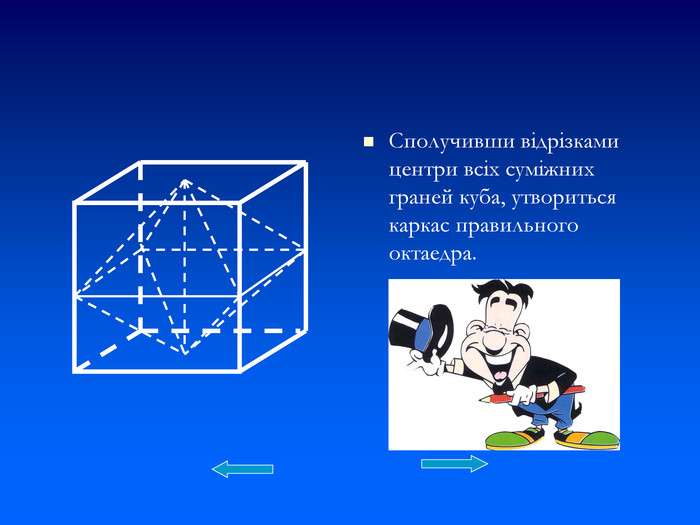
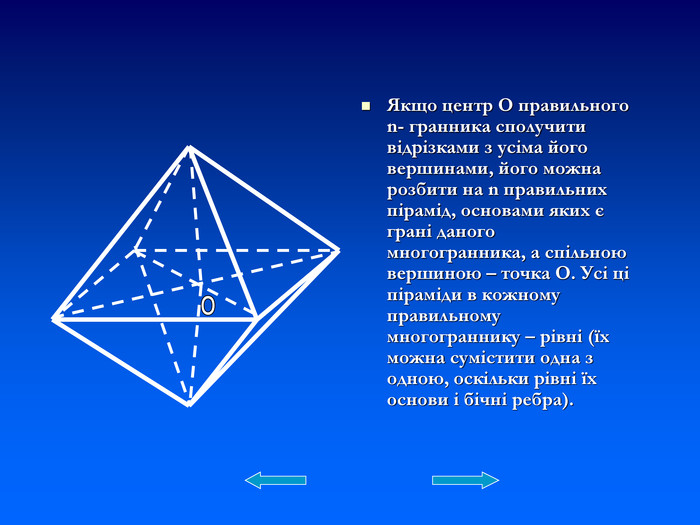
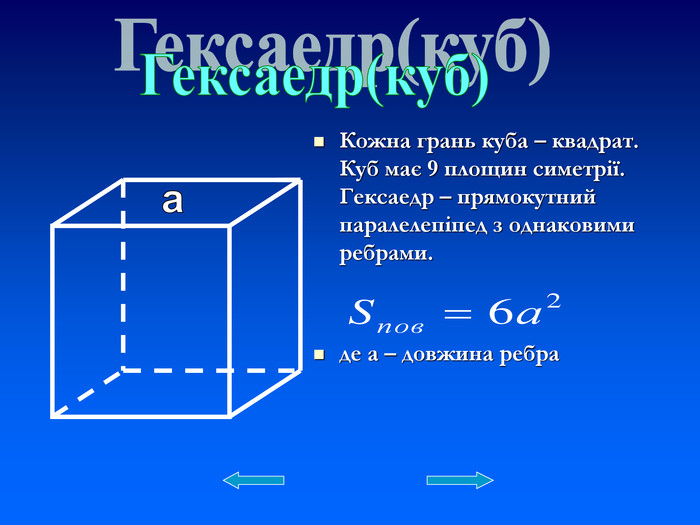
Презентація. Тема "Правильні многогранники".
Про матеріал
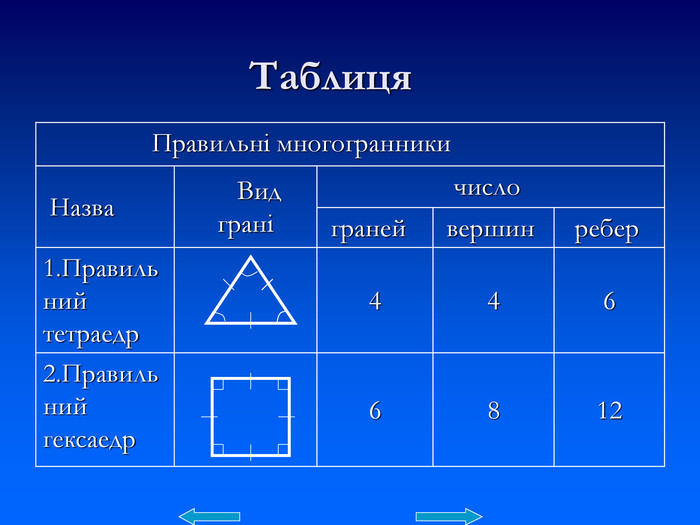
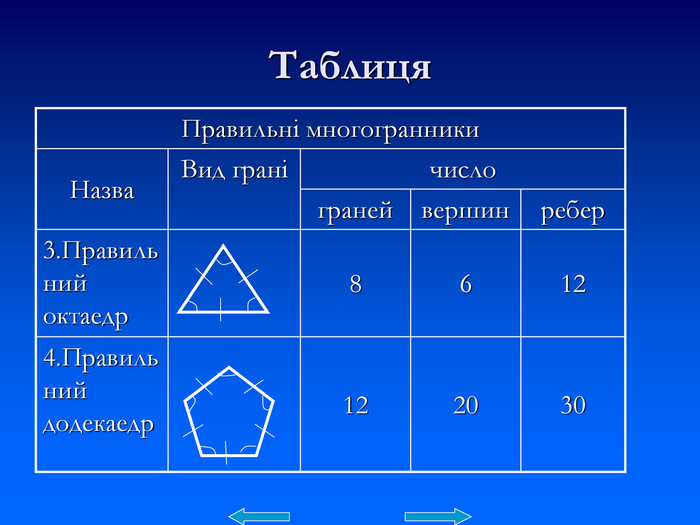
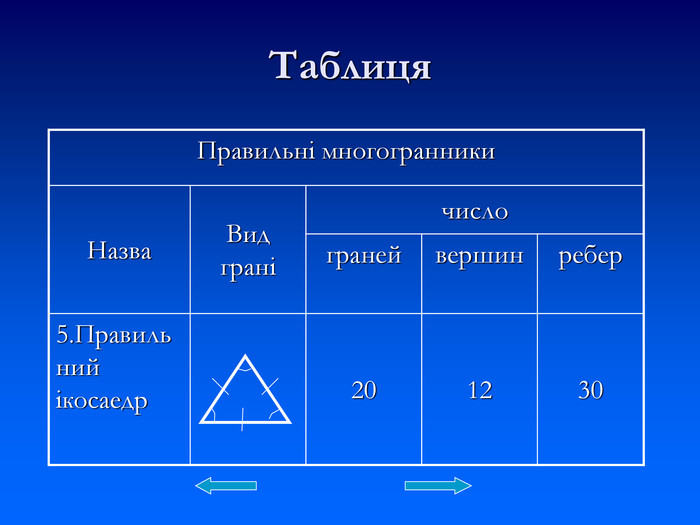
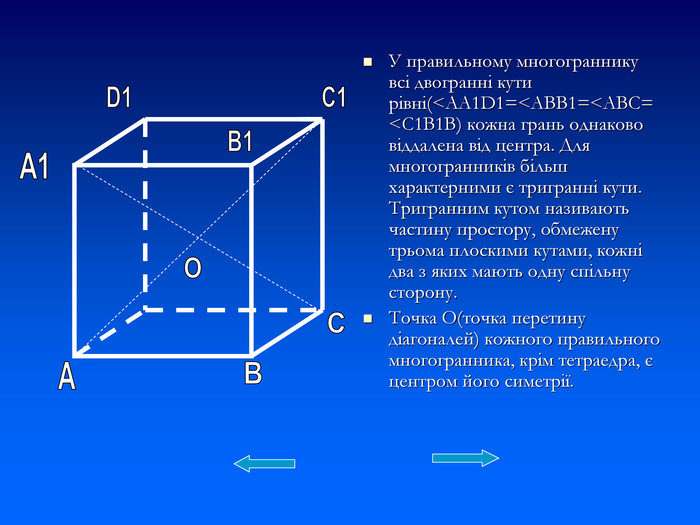
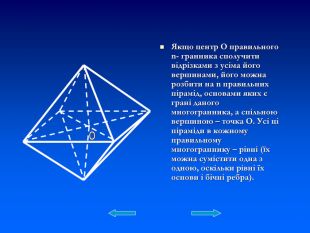
Презентація "Правильні многогранники" познайомить із видами та формою правильних многогранників. Презентація містить таблиці характерні для кожного виду правильного многогранника та деякі формули. Презентація розрахована на учнів які цікавляться позапрограмовим матеріалом. Її можна використати на факультативах та додаткових заняттях з геометрії. Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку