Презентація "Теорема Піфагора у техніці і не тільки"
Про матеріал
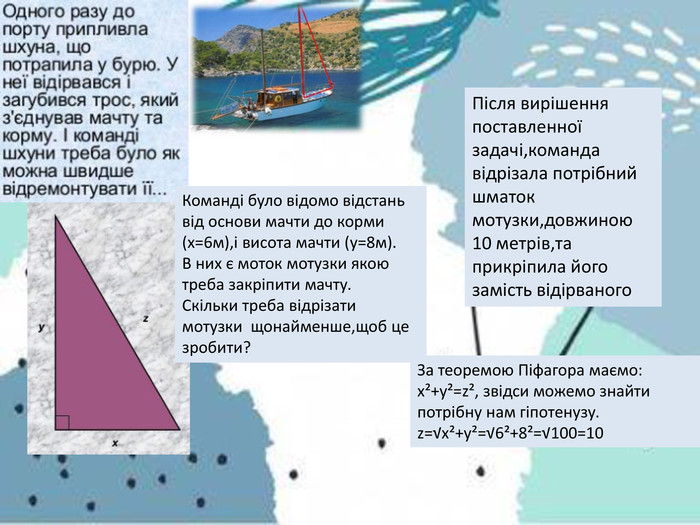
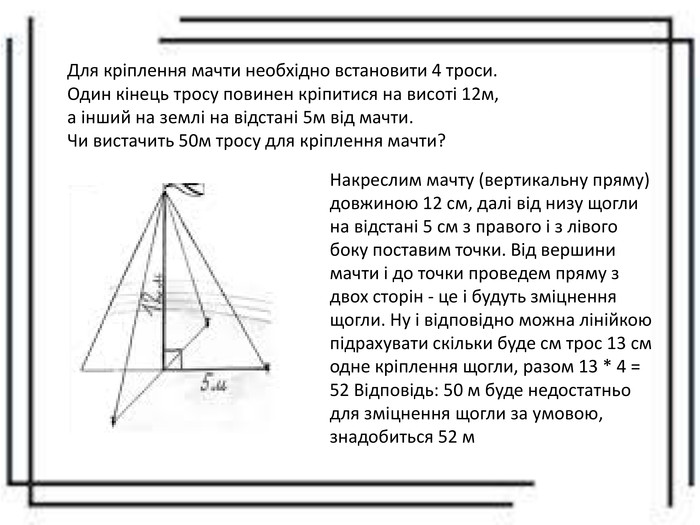
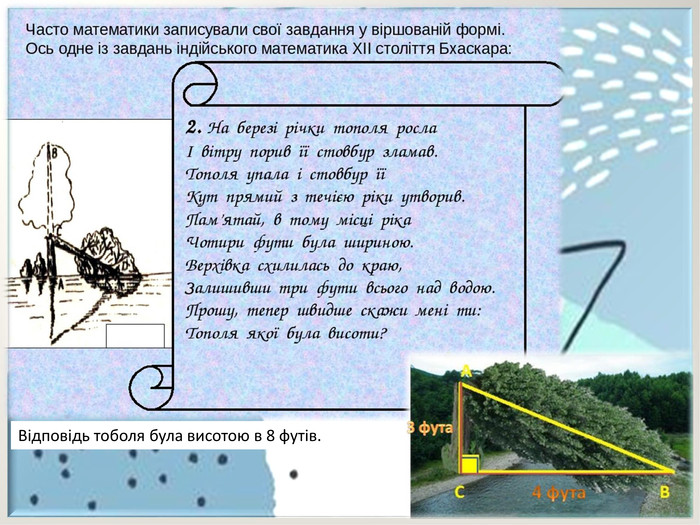
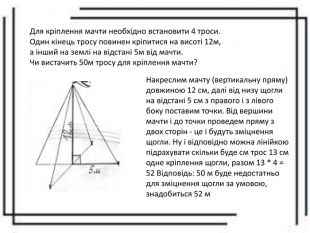
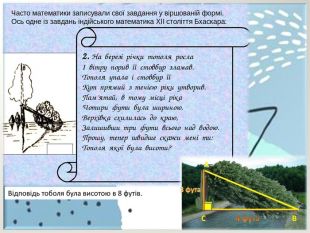
Учнівський проєкт "Застосування теореми Піфагора у техніці і не тільки". У роботі учні демонструють цікаві сторони застосування теореми Піфагора у прикладних задачах. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку