Презентація " Теорема синусів і теорема косинусів. Прикладні задачі"
Про матеріал
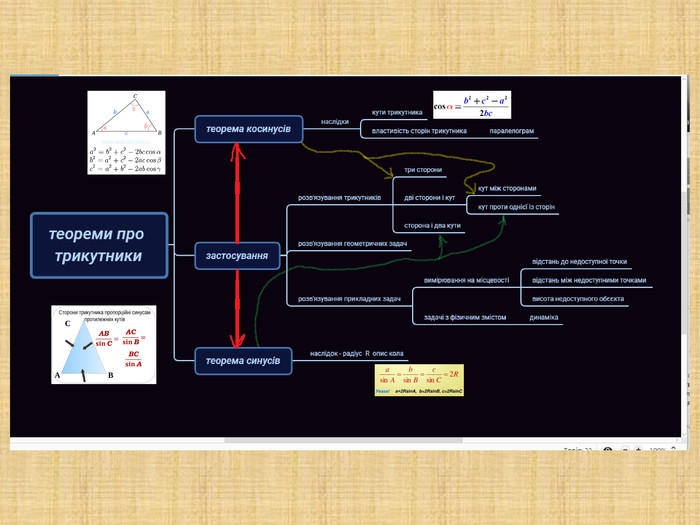
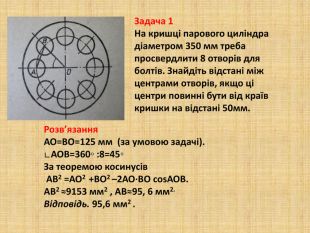
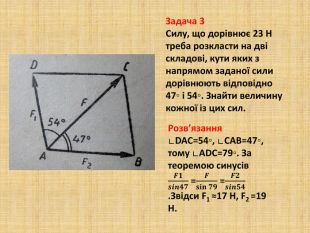
Презентація -супровід до уроку розв'язування прикладних задач на застосування теореми синусів і теореми косинусів. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже гарна презентація!! Практичні задачі це велика цінність.
-
-
Дуже класна презентація. Цікаво, де Ви знаходите такі задачі. Єдине, у першій задачі, у відповіді одиниці вимірювання лінійні, а не квадратні, мабуть не звернули увагу.
pptx
До підручника
Геометрія 9 клас (Єршова А. П., Голобородько В.В., Крижановський О.Ф., Єршов С. В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку