Конспект уроку і презентація до уроку "Відстань між двома точками із заданими координатами"

 УРОК №

ТЕМА:  ВIДСТАНЬ МIЖ ДВОМА ТОЧКАМИ IЗ ЗАДАНИМИ КООРДИНАТАМИ.

Мета: домогтися  засвоєння учнями змiсту теореми, що виражає формулу вiдстанi мiж двома точками в прямокутнiй системi координат, а також способу її доведення, сформувати в учнiв уявлення про сферу застосування формули вiдстанi мiж двома точками, сформувати вмiння вiдтворювати вивчену формулу, записувати  її  вiдповiдно до умови задачi, а також використовувати для розв’язу
вання задач на обчислення, розвивати пам'ять, увагу, логічне мислення

Тип уроку: засвоєння нових знань, умiнь, навичок.

 

ХІД УРОКУ

I. Органiзацiйний етап

II. Перевiрка домашнього завдання

Тестовая самостійна робота з подальшою взаємоперевiркою

1.  Яке твердження неправильне?
    1) Якщо точка лежить на осi абсцис, то її ордината дорiвнює нулю.
    2) Якщо точка лежить на осi ординат, то її абсциса дорiвнює нулю.
    3) Кожна координата середини вiдрiзка дорiвнює сумi вiдповiдних координат

       його кiнцiв.
    4) Абсциса й ордината початку координат дорiвнюють нулю.

2.  Точка C - середина вiдрiзка AB. Знайдiть її координати, якщо A(2; 4); B(4; 2).

     а) (6; 6);      б) (3; 6);      в) (3;3);     г(−3;−3).

3.  У трикутнику ABC проведено медiану BM. Знайдiть координати точки M, якщо

     A(0;3); C(-4;-5).

     а) (4; −7);     б) (-2; -1);   в) (-4; -2);    г) (4; −4).  

4.  AB—дiаметр кола з центром у точцi O. Знайдiть координати точки B, якщо

     A(0; 2);  O(2; 1).

         а) (4; 0);     б) (2; 2);     в) (4; 4);     г) (0; 4).

5.  Знайдiть координати точки перетину дiагоналей квадрата ABCD, якщо

     A(0;4), C(4;0).

    а)  (4; 4);     б) (0; 2);    в) (4; 0);     г) (2; 2).

 

ІІІ. Актуалізація опорних знань.

Інтерактивна гра «Математичне лото»

1. Знайдіть відстань між парами точок зображених на рисунку

 

 

 

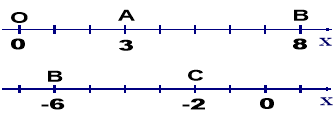
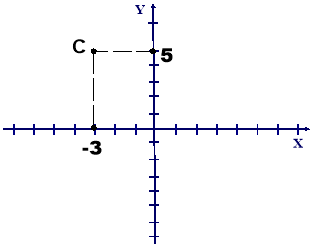
2. Знайдіть відстань  від т. С до осі абсцис?

   Знайдіть відстань  від т. С до осі ординат?

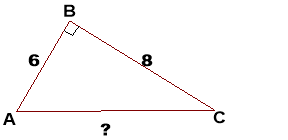3. Знайдіть довжину сторони АС?

  

 

 

 

4. Знайдіть довжину відрізка АВ

1) А (3;1),  В (7;1);        2) А (5;2),  В (5;8);       3) А (0;4),  В (3;0).

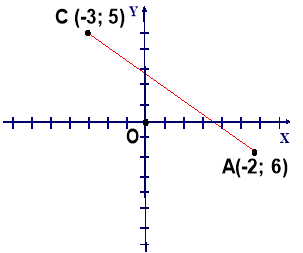IV. Мотивація навчальної діяльності.

      Проблемне завдання

Знайдіть відстань між т. С і А.

 

 

V. Засвоєння нових знань і вмінь.

Розв’язуємо разом

1. Дано точки A (−2; 1), B (0; 4), C (4; 1),

D (2 ; -2;). Доведiть, що ABCD — паралелограм.

2. Знайдiть x, якщо вiдстань мiж точками M (2; 1) і N (x; -2) дорiвнює 5.

 

 

Робота в парах

Картка №1

У трикутнику АВС т. А (3;-1), В(-5;7), С (1;5). Знайдіть довжину середньої лінії КР трикутника АВС, де т. К і Р – середини сторін АВ і ВС відповідно.

 

Картка №2

Вершини трикутника знаходяться в точках із координатами (5;1), (7;2), (9;-2). Знайдіть площу цього трикутника.

 

Картка №3

Знайдіть координати точки, яка поділяє відрізок АВ у відношенні 3: 1,  рахуючи від т. А, якщо А(3; -5) і В (-1;7).

Додатково:

Знайдіть довжини сторін трикутника, якщо відомі координати середин його сторін (5;1),  (9;4),  (9;-2).

Працюємо самостійно.

Аукціон задач.

1.  Знайдіть відстань між точками А і В, якщо А (-1;2) і В (4; -3).                      0,5  б.

2.  Доведіть, що т. М (0; -1) є центром кола, описаного навколо трикутника АВС, якщо А (6; - 9), В (-6; 7), С (8; 5).                                                                               1 б.

3. Знайдіть периметр трикутника, вершини якого знаходяться в точках із координатами (1;2), (8; 26), (19; 26).                                                                         1 б.

Точки А(1;4),  В(9;6), С (9;4) – вершини трикутника. Доведіть, що трикутник АВС – прямокутний.

4. Чи існує трикутник, вершини якого знаходяться в точках із координатами (3; 4), (-1; 6), (1; 5)?                                                                                                                 2 б.

5. При якому значенні х відстань між точками С (3; 2) і D (x; -1) дорівнює 5?     2 б.

6.  Вершини трикутника є точки А (-1; 3), В (5; 9), С (6; 2). Доведіть, що трикутник АВС- рівнобедрений.                                                                                                  2 б.

7.   У трикутнику АВС т. А (3;-1), В(-5;7), С (1;5). Знайдіть довжину середньої лінії КР трикутника АВС, де т. К і Р – середини сторін АВ і ВС відповідно.               2 б.

8. Знайдіть координати вершини А рівностороннього трикутника АВС, якщо відомі координати вершин В (-2; 0) і С (4; 0).                                                                      3 б.

9. Всередині квадрата АВС D існує така точка М, що МА=7, МВ=13, МС=17. Знайдіть довжини сторони і діагоналі квадрата.                                                     5 б.  

 

VІ. Підсумок уроку.

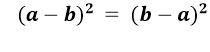Дайте відповіді на запитання лише «так» чи «ні».

1. Чи правильно, що

     2) Чи правильно, знайдена відстань між т. А (-2;1) і т. В (0;4)?

 

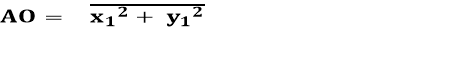
    3) Якщо  А (х₁, у₁)    О (0; 0),  то

   4) Чи правильно, знайдена відстань між т. А (3; 4) і т. В (2; -1)?

 

VІІ. Рефлексія. У вас на партах лежать смайлики. Як ви охарактеризуєте свій емоційний стан під час уроку.

VІІІ. Домашнє завдання. §8, стор. 77-78 (вчити), №8.2; 8.5; 8.10; 8.12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Картка №1

У трикутнику АВС т. А (3;-1), В(-5;7), С (1;5). Знайдіть довжину середньої лінії КР трикутника АВС, де т. К і Р – середини сторін АВ і ВС відповідно

 

 

Картка №2

Вершини трикутника знаходяться в точках із координатами (5;1), (7;2), (9;-2). Знайдіть площу цього трикутника.

 

 

 

 

Картка №3

Знайдіть координати точки, яка поділяє відрізок АВ у відношенні 3: 1,  рахуючи від т. А, якщо А(3; -5) і В (-1;7).

 

 

 

 

 

5	4
-4	-3
3	6

 

Опорний конспект

Приклад: Знайдіть довжину відрізку CD, якщо т. С (4; 1), т. D (2 ; -2;).

Приклад:  Знайдіть координати середини відрізка ВС, якщо В (5; 4), С (3; 2).                     хс =            ус =       т. С (4; 3)

10	10
10	10
10	10

 

Аукціон задач

 

1.  Знайдіть відстань між точками А і В, якщо А (-1;2) і В (4; -3).

                                                                                                                   0,5  б.

2.  Доведіть, що т. М (0; -1) є центром кола, описаного навколо трикутника АВС, якщо А (6; - 9), В (-6; 7), С (8; 5). 

                                                                                                                       1 б.

3. Знайдіть периметр трикутника, вершини якого знаходяться в точках із координатами (1;2), (8; 26), (19; 26).    

                                                                                                                       1 б.

4. Чи існує трикутник, вершини якого знаходяться в точках із координатами (3; 4), (-1; 6), (1; 5)?  

                                                                                                                       2 б.

5. При якому значенні х відстань між точками С (3; 2) і D (x; -1) дорівнює 5?                                                                                               

                                                                                                                       2 б.

6.  Вершини трикутника є точки А (-1; 3), В (5; 9), С (6; 2). Доведіть, що трикутник АВС- рівнобедрений.

                                                                                                                      2 б.

7.   У трикутнику АВС т. А (3;-1), В(-5;7), С (1;5). Знайдіть довжину середньої лінії КР трикутника АВС, де т. К і Р – середини сторін АВ і ВС відповідно.           

                                                                                                                      2 б.

8. Знайдіть координати вершини А рівностороннього трикутника АВС, якщо відомі координати вершин В (-2; 0) і С (4; 0). 

                                                                                                                      3 б.

9. Всередині квадрата АВС D існує така точка М, що МА=7, МВ=13, МС=17. Знайдіть довжини сторони і діагоналі квадрата.

                                                                                                                      5 б.

Оціночний лист учня _______________________________

Завдання	Тестова робота   (1 б.)	Математичне лото            (0,1 б)	Робота в парі     (2 б.)	Аукціон задач	Додаткові бали	Всього
Отримані бали

 

 

 

 

 

Оціночний лист учня _______________________________

Завдання	Тестова робота   (1 б.)	Математичне лото            (0,1 б)	Робота в парі     (2 б.)	Аукціон задач	Додаткові бали	Всього
Отримані бали

 

 

 

 

 

Оціночний лист учня _______________________________

Завдання	Тестова робота   (1 б.)	Математичне лото            (0,1 б)	Робота в парі     (2 б.)	Аукціон задач	Додаткові бали	Всього
Отримані бали