Презентація Теореми ферма, Ролля, Лагранжа

ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ

П'єр Ферма П'єр де Ферма (1601-1665) - французький математик-самоук, один з творців аналітичної геометрії, математичного аналізу, теорії ймовірностей і теорії чисел. За професією юрист, поліглот. Автор Великої теореми Ферма, «найзнаменитішою математичної загадки всіх часів».

Мішель Ролль (1652-1719) Французький математик, член Паризької академії наук. Основні праці присвячені методам чисельного розв’язування рівнянь. Більшість наукових здобутків М. Ролля не були помічені науковою спільнотою за його життя; їх оцінили значно пізніше. Мішель Ролль

Жозеф Луї Лагранж Жозеф Луї Лагранж (1736-1813) Французький математик, механік і астроном, президент Берлінської академії наук, член Паризької академії наук. Основні праці — у галузі математичного аналізу, варіаційного числення, алгебри, теорії чисел, диференційних рівнянь, механіки. Кавалер ордена Почесного легіону.

ТЕОРЕМА 1 (Ферма). Нехай функція y = f(x) визначена на проміжку [a; b] і в точці хо(a; b) набуває свого найменшого (найбільшого) значення. Тоді, якщо функція f є диференційовною в точці хо , тобто існує f (хо) , то f (хо) = 0 . ГЕОМЕТРИЧНИЙ ЗМІСТ теореми Ферма Дотичні, проведені у точках, де функція набуває найбільшого (найменшого) значення, будуть горизонтальними прямими. Оскільки кутовий коефіцієнт горизонтальної прямої дорівнює нулю, то f (хо) = 0 і g (хо) = 0.

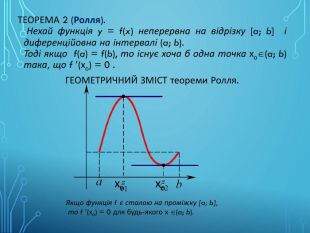
ТЕОРЕМА 2 (Ролля). Нехай функція y = f(x) неперервна на відрізку [a; b] і диференційовна на інтервалі (a; b). Тоді якщо f(a) = f(b), то існує хоча б одна точка хо(a; b) така, що f (хо) = 0 . ГЕОМЕТРИЧНИЙ ЗМІСТ теореми Ролля. хо хо Якщо функція f є сталою на проміжку [a; b], то f (хо) = 0 для будь-якого х (a; b).

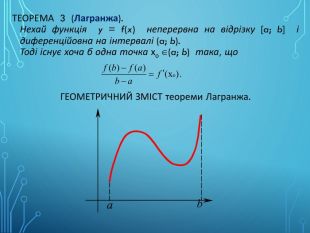
ТЕОРЕМА 3 (Лагранжа). Нехай функція y = f(x) неперервна на відрізку [a; b] і диференційовна на інтервалі (a; b). Тоді існує хоча б одна точка хо (a; b) така, що ГЕОМЕТРИЧНИЙ ЗМІСТ теореми Лагранжа.

ГЕОМЕТРИЧНИЙ ЗМІСТ теореми Лагранжа. Якщо функція y = f(x) задовольняє вказаним в теоремі умовам, то на інтервалі (a; b) існує хоча б одна точка хо така, що у відповідній ій точці графіка функції y = f(x) дотична паралельна січній AB.

Теорема Лагранжа є узагальненням теореми Ролля. Якщо f(a) = f(b), то за теоремою Лагранжа Теореми Ролля і Лагранжа не вказують, як знайти точку хо. Вони лише гарантують, що існує точка з певною властивістю.

Підручник з алгебри (поглиблене вивчення) для 10 класу, автори: Мерзляк А. Г., Номіровський Д. А., Полонський В. Б., Якір М. С., 2018р.

Якщо функція набуває свого найменшого або найбільшого значення, то f (хо) = 0.

ДОМАШНЄ ЗАВДАННЯ