Презентація "Тіла обертання"
















Куля. Куля - тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу. Поверхня кулі називається сферою. Також дуже часто кулею називають частину простору, обмежену сферою. Куля утворюється при обертанні півкруга навколо його діаметра як осі. Цей діаметр називають віссю кулі, а його кінці — полюсами кулі. Відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі. Площа сфери та об'єм куліПереріз кулі площиною. Сегмент. Сектор. Зріз
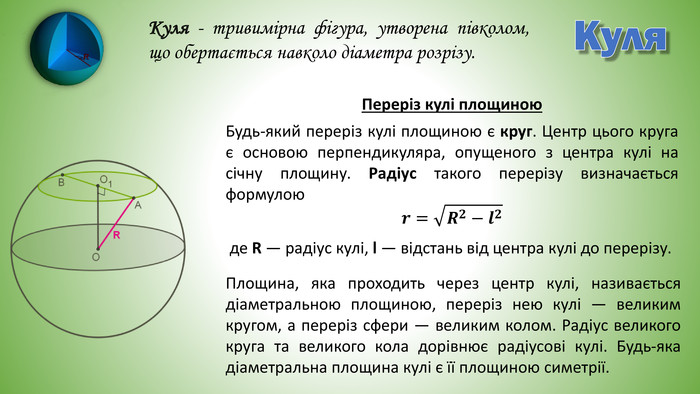
Куля. Куля - тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу. Будь-який переріз кулі площиною є круг. Центр цього круга є основою перпендикуляра, опущеного з центра кулі на січну площину. Радіус такого перерізу визначається формулою де R — радіус кулі, l — відстань від центра кулі до перерізу.𝒓=𝑹𝟐−𝒍𝟐 Переріз кулі площиною. Площина, яка проходить через центр кулі, називається діаметральною площиною, переріз нею кулі — великим кругом, а переріз сфери — великим колом. Радіус великого круга та великого кола дорівнює радіусові кулі. Будь-яка діаметральна площина кулі є її площиною симетрії.
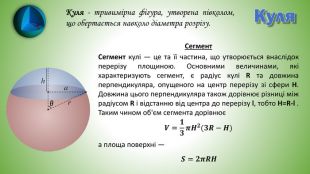
Куля. Куля - тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу. Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною. Основними величинами, які характеризують сегмент, є радіус кулі R та довжина перпендикуляра, опущеного на центр перерізу зі сфери H. Довжина цього перпендикуляра також дорівнює різниці між радіусом R і відстанню від центра до перерізу l, тобто H=R-l . Таким чином об'єм сегмента дорівнюєа площа поверхні —𝑽=𝟏𝟑𝝅𝑯𝟐(𝟑𝑹−𝑯) Сегмент𝑺=𝟐𝝅𝑹𝑯
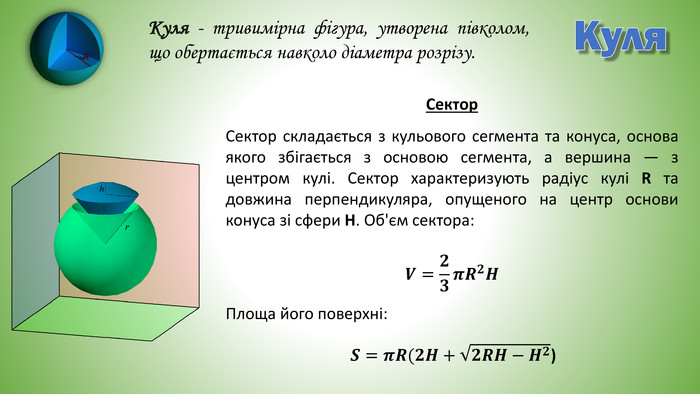
Куля. Куля - тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу. Сектор складається з кульового сегмента та конуса, основа якого збігається з основою сегмента, а вершина — з центром кулі. Сектор характеризують радіус кулі R та довжина перпендикуляра, опущеного на центр основи конуса зі сфери H. Об'єм сектора: Площа його поверхні:𝑽=𝟐𝟑𝝅𝑹𝟐𝑯 Сектор𝑺=𝝅𝑹(𝟐𝑯+𝟐𝑹𝑯−𝑯𝟐)
Куля. Куля - тривимірна фігура, утворена півколом, що обертається навколо діаметра розрізу. Зріз (кульовий шар) — це стереометричне тіло, утворене перерізами кулі двома паралельними площинами. Він характеризується такими величинами: Радіус відповідної кулі, R;Відстань між двома перерізами, H;Радіуси обох перерізів, 𝒓𝟏, 𝒓𝟐. Об'єм зрізу визначається формулою Площа його поверхні:𝑽=𝟏𝟔𝝅𝑯𝟑+𝟏𝟐𝝅(𝒓𝟏𝟐+𝒓𝟐𝟐)𝑯 Зріз𝑺=𝟐𝝅𝑹𝑯
Циліндр Циліндр - тривимірна фігура, утворена прямокутником, що обертається навколо однієї із сторін. Круги, що утворюють циліндр називаються основами циліндра. Вони рівні і лежать у паралельних площинах. Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні між собою. Поверхня циліндра складається з основ і бічної поверхні. Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами основ. Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним. Площа та об'єм циліндра. Переріз циліндра
Циліндр Циліндр - тривимірна фігура, утворена прямокутником, що обертається навколо однієї із сторін. Розгортка циліндра являє собою прямокутник з висотою h і довжиною 2πR, отже площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:𝑺𝒃=𝟐𝝅𝑹𝒉 Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та його основ:𝑺𝒑=𝟐𝝅𝑹(𝒉+𝑹) Площа та об'єм циліндра. Об’єм циліндра дорівнює: 𝑽=𝝅𝑹𝟐𝒉=𝝅𝒅𝟐𝟒𝒉
Циліндр Циліндр - тривимірна фігура, утворена прямокутником, що обертається навколо однієї із сторін. RαПереріз, який утворився при перетині циліндра заданою площиною називається еліпсом з великою піввіссю 𝒂=𝑹𝐜𝐨𝐬𝜶 і малою піввіссю b=R, тому його площа: 𝑺𝒑=𝝅𝑹𝟐cos𝜶 Осьовим перерізом циліндра є прямокутник, що проходить через вісь циліндра. Його площа:𝑺𝒐𝒑=𝟐𝑹𝒉=𝑫𝒉 Rh. Переріз циліндра
Конус. Конус — тривимірна фігура, утворена прямокутним трикутником, що обертається навколо одного з катетів. Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Відрізок, що сполучає вершину конуса з точкою границі його основи називається твірною конуса Множина всіх твірних конуса називається бічною поверхнею конуса. Якщо основою конуса є круг, то конус називають круговим. Площа та об'єм конуса. Зрізаний конус. Прості перерізи конуса. Конічні перерізи конуса
Конус. Конус — тривимірна фігура, утворена прямокутним трикутником, що обертається навколо одного з катетів. Площа бічної поверхні зрізаного конуса. Довжина твірної𝑺𝒃=𝝅𝒍(𝑹+𝒓) 𝒍=𝒉𝟐+(𝑹−𝒓)𝟐 Зрізаний конус. Об'єм зрізаного кругового конуса𝑽=𝟏𝟑𝝅𝒉(𝑹𝟐+𝑹𝒓+𝒓𝟐) Зрізаний ко́нус — геометричне тіло, що знаходиться між площиною, що перетинає конус паралельною до його основи і самою основою
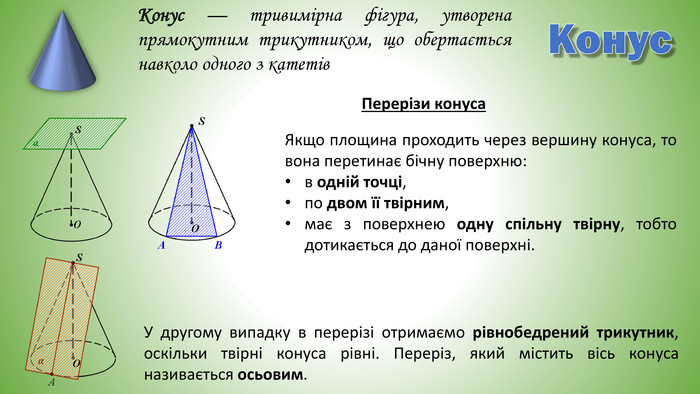
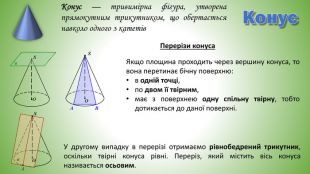
Конус. Конус — тривимірна фігура, утворена прямокутним трикутником, що обертається навколо одного з катетів. Перерізи конуса. У другому випадку в перерізі отримаємо рівнобедрений трикутник, оскільки твірні конуса рівні. Переріз, який містить вісь конуса називається осьовим. Якщо площина проходить через вершину конуса, то вона перетинає бічну поверхню:в одній точці, по двом її твірним, має з поверхнею одну спільну твірну, тобто дотикається до даної поверхні.
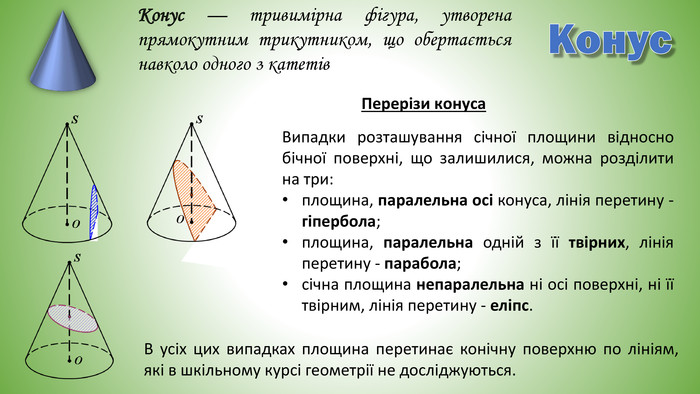
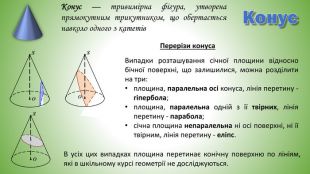
Конус. Конус — тривимірна фігура, утворена прямокутним трикутником, що обертається навколо одного з катетів. Перерізи конуса. В усіх цих випадках площина перетинає конічну поверхню по лініям, які в шкільному курсі геометрії не досліджуються. Випадки розташування січної площини відносно бічної поверхні, що залишилися, можна розділити на три:площина, паралельна осі конуса, лінія перетину - гіпербола;площина, паралельна одній з її твірних, лінія перетину - парабола;січна площина непаралельна ні осі поверхні, ні її твірним, лінія перетину - еліпс.
Тор. Тор — тривимірна фігура, утворена колом, що обертається навколо прямої, яка не перетинає його. Тор — геометричне тіло, що утворюється обертанням кола навколо осі, котра лежить у одній площині з колом, але не перетинає його. Форма тора зовні нагадує бублик. З топологічної точки зору тор - це замкнута поверхня, яка визначається як добуток двох кіл: S¹ × S¹.Інтуїтивно це означає, що траєкторія, що спочатку обходить «дірку» тора, а потім його тіло може бути деформована у траєкторію, що спочатку обходить тіло тора, а потім - дірку. Таким чином, обходи тора «по широті» та «по довготі» комутують. Площа та об'єм тора
Тор. Тор — тривимірна фігура, утворена колом, що обертається навколо прямої, яка не перетинає його. Площа поверхні тора. Об’єм тора. Площа та об'єм тора𝑺=𝟒𝝅𝟐𝑹𝒓=(𝟐𝝅𝑹)(𝟐𝝅𝒓) 𝑽=𝟐𝝅𝟐𝑹𝒓𝟐=(𝝅𝒓𝟐)(𝟐𝝅𝑹) Ці формули точно збігаються з формулами для площі та об'єму циліндра з висотою 2πR та радіусом r, який утворюється при розрізанні тора та випрямленні його вздовж лінії, що проходить через центр труби. Втрати площі та об'єму на внутрішньому боці тора точно компенсуються збільшенням площі та об'єму на зовнішньому боці.
Об'єм і площа поверхні тіл обертання можна дізнатися за допомогою теорем Гульдіна-Паппа. Перша теорема Гульдіна-Паппа стверджує: Наприклад, для тора радіусом R i з радіусом кола r, довжина лінії s=2πr, довжина кола для центру мас l=2πR, звідки площа поверхні тора 𝒔∙𝒍=𝟒𝝅𝟐𝒓𝑹. Теореми Гульдіна-Паппа. Площа поверхні, утвореної при обертанні лінії, що лежить в площині цілком по одну сторону від осі обертання, дорівнює добутку довжини лінії s на довжину кола l = 2πrs, яке пробігає центр мас (т. С) цієї лінії.
Об'єм і площа поверхні тіл обертання можна дізнатися за допомогою теорем Гульдіна-Паппа. Друга теорема Гульдіна-Паппа стверджує: Наприклад, для тора радіусом R i з радіусом кола r, площа кола 𝑨=𝝅𝑹𝟐, довжина кола обертання центру мас 𝒍=𝟐𝝅𝑹, звідси об'єм тора 𝑨∙𝒍=𝟐𝝅𝟐𝒓𝟐𝑹 Теореми Гульдіна-Паппа. Об'єм тіла, утвореного при обертанні фігури, що лежить в площині цілком по одну сторону від осі обертання, дорівнює добутку площі А фігури на довжину кола l = 2πRs, яке пробігає центр мас (т. CA) цієї фігури.


про публікацію авторської розробки
Додати розробку


















-

Котовський Євгеній
21.01.2024 в 11:10
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
4.0
-

Крупник Людмила Віталіївна
20.10.2023 в 18:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kosyhina Elena
01.04.2023 в 20:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Молоткова Татьяна
11.09.2021 в 17:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Малець Ірина Василівна
17.02.2021 в 20:53
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 2 відгука