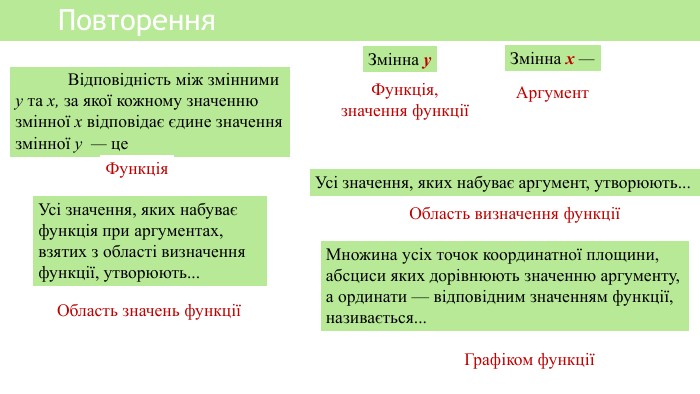
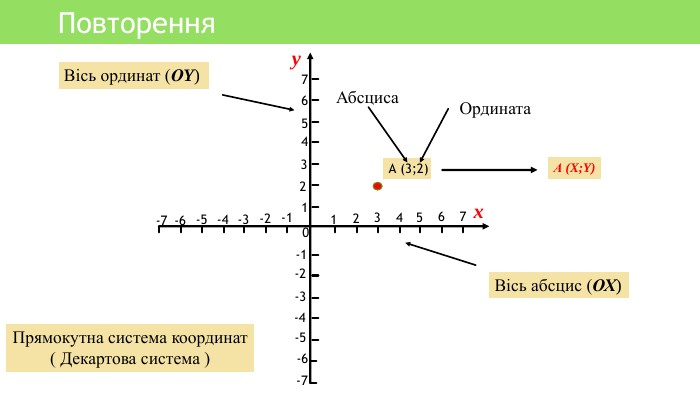
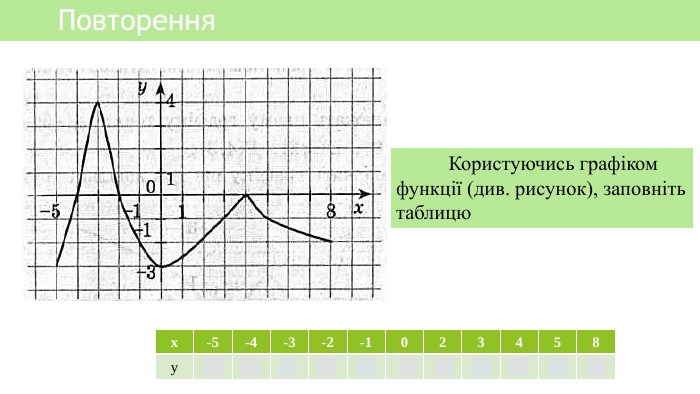
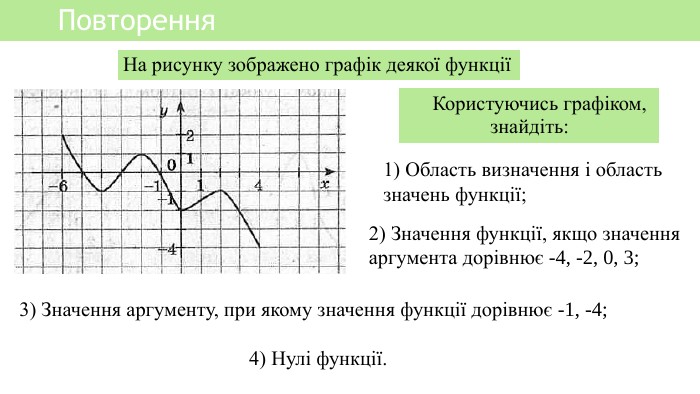
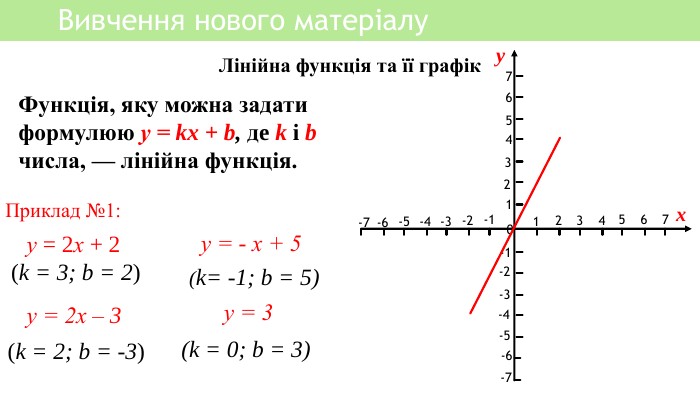
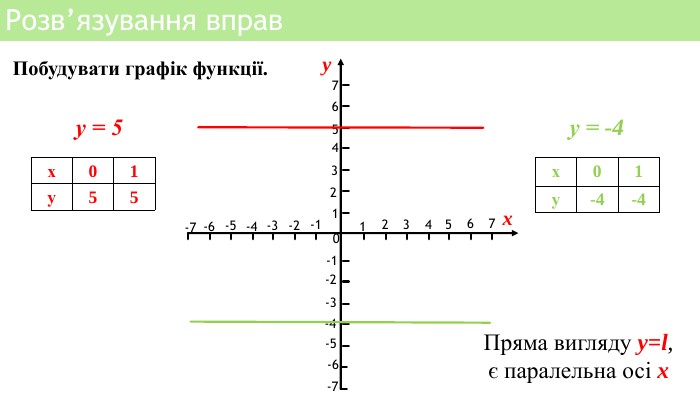
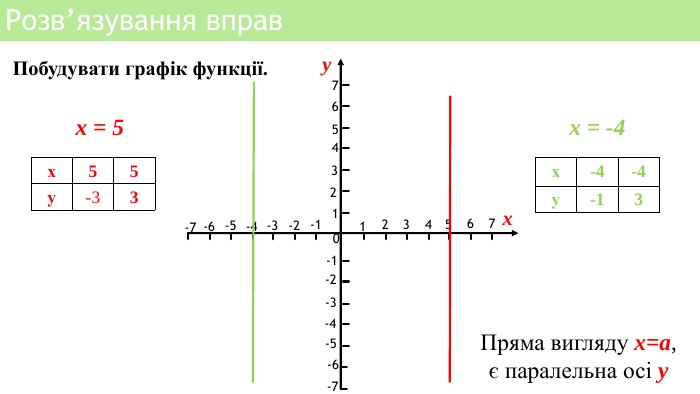
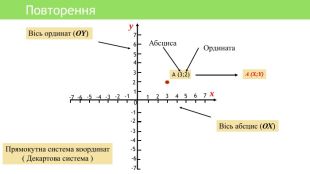
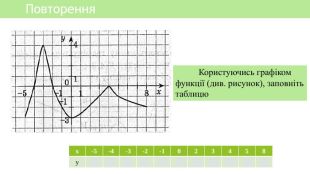
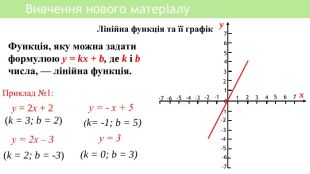
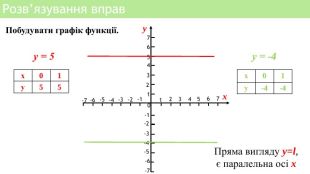
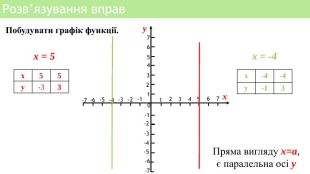
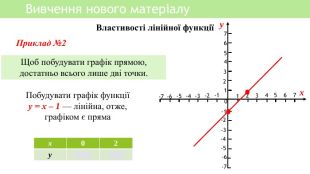
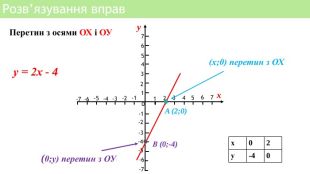
Презентація уроку алгебри "Лінійна функція, її властивості і графік"
Про матеріал
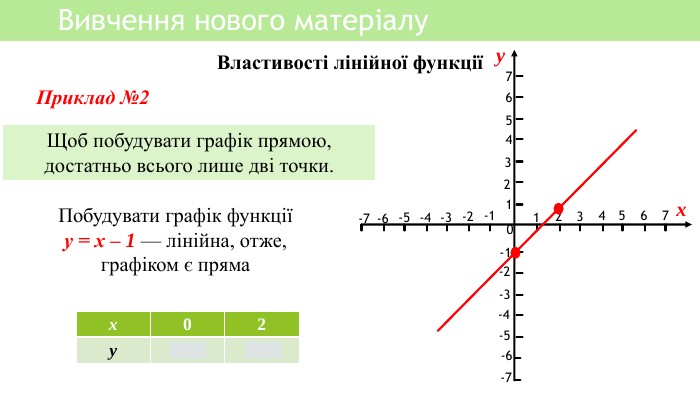
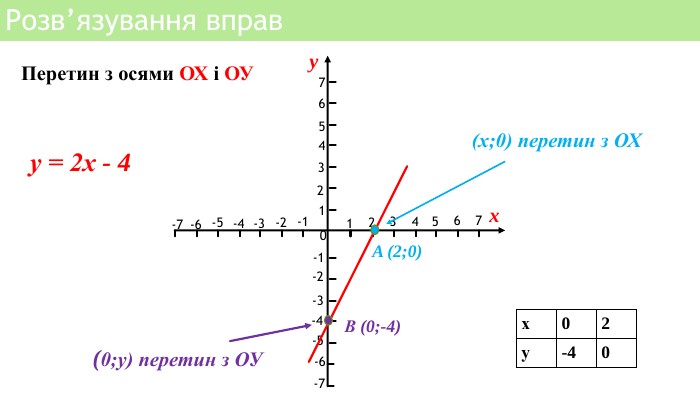
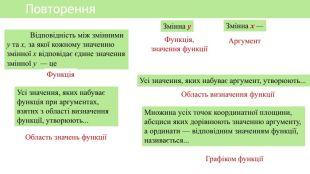
Презентація уроку алгебри з теми Лінійна функція, підійде для дистанційного уроку. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку