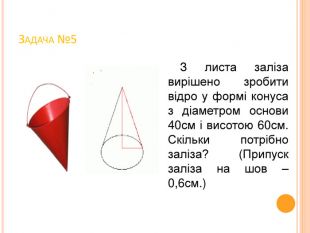
Презентація уроку на тему: "Навчальні проекти:Тіла обертання навколо нас! Розв'язування прикладних задач"

«Ми живемо в геометричний період і навкруги нас – геометрія» Лє Корбюзьє

Тема уроку: Навчальні проекти з теми: «Тіла обертання навколо нас!». Розв’язування прикладних задач. Підготувала вчитель математики Монастириського ЗЗСО І-ІІІ ст. Синюк Наталія Іванівна

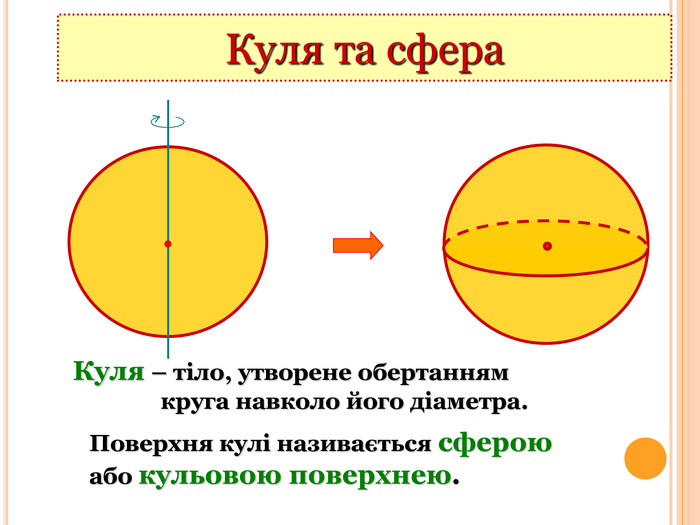
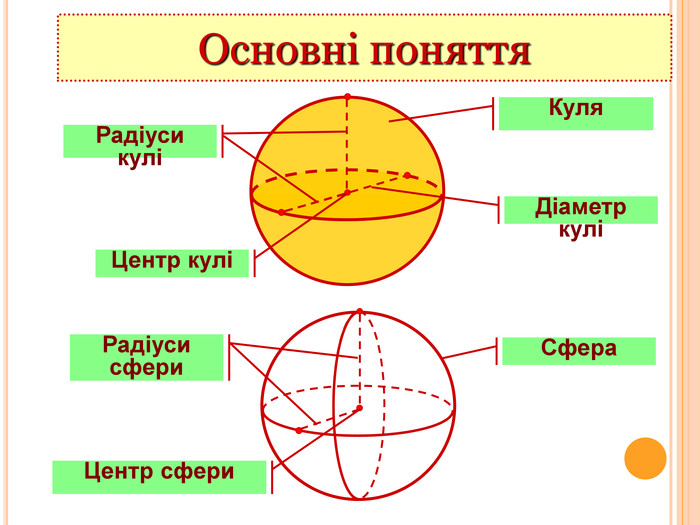
Важливим чинником розвитку особистості є формування в учнів умінь застосовувати набуті знання у реальних життєвих ситуаціях. У наш час немає такої галузі науки, де не застосовують досягнень математики. Під час виконання навчальних проектів з теми «Многогранники» учні одинадцятих класів працювали групами, розділяли ролі, вчилися взаємодіяти в колективі, шукати та аналізувати інформацію, застосовувати набуті знання на практиці, презентувати власні напрацювання на загал. На цих заняттях учні самостійно виготовляли вироби, проводили виміри та звітували за виконану роботу. Виготовлені шедеври прикрашають кабінет математики Монастириської ЗОШ І-ІІІ ступенів.

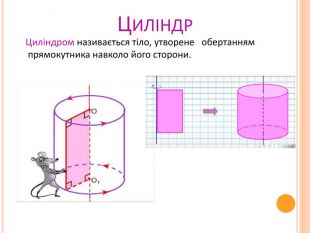
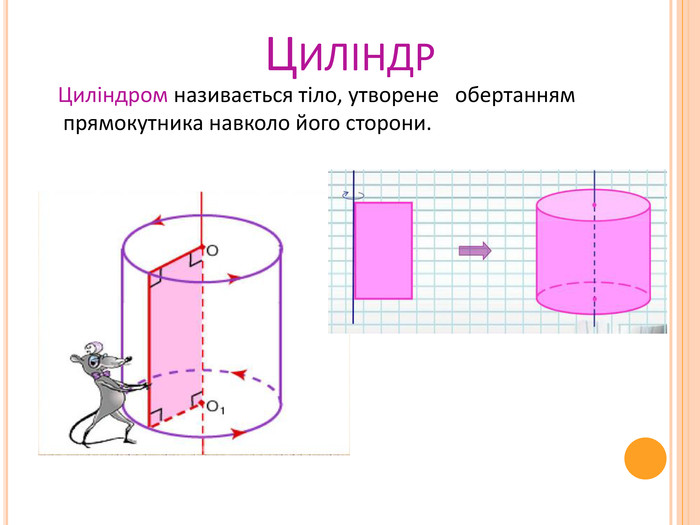
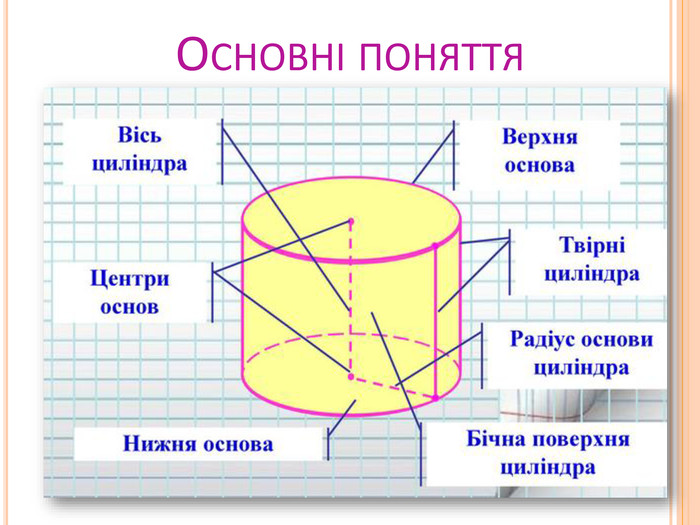
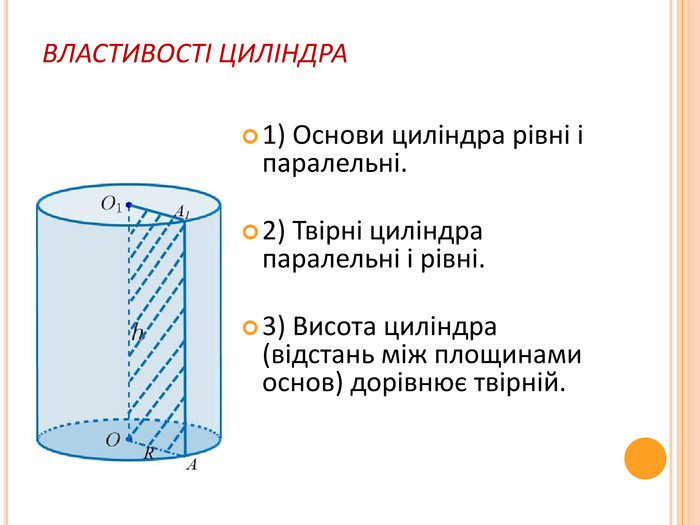
Світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творіннями природи й людини. Геометрія є могутнім інструментом пізнання природи і створення техніки. Вона виявляється скрізь, де потрібна найменша точність у визначенні форми і розмірів. Техніку, інженеру, робітнику, архітектору, автослюсарю – всім необхідна геометрична уява. Багатогранники знаходять широке застосування у повсякденному житті, науці і техніці.

ІСТОРІЯ ВИНИКНЕННЯ ТА ВИВЧЕННЯ ТІЛ ОБЕРТАННЯ

Початкові відомості про властивості геометричних тіл люди знайшли, спостерігаючи навколишній світ і в результаті практичної діяльності.  До Фалеса в світі геометрією майже ніхто не займався. У геометричних фігур не було назв. Тому люди почали вигадувати їм свої назви.

Розвиток геометрії Геометрія в ранній період свого розвитку досягла особливо високого рівня в Єгипті. Ученим того часу вдалося дістати ряд визначних результатів. У першому тисячолітті до нашої ери геометричні відомості від єгиптян перейшли до греків. За період з VII по III століття до нашої ери грецькі геометри не тільки збагатили геометрію численними новими теоремами, але зробили також серйозні кроки до суворого її обгрунтування. Багатовікова робота грецьких вчених за цей період була підсумована Евклідом в його знаменитій праці «Початки».

ВСІ ДОСЛІДЖЕННЯ ОПИСАНІ У ТРАКТАТІ АРХІМЕДА «ПРО КУЛІ І ЦИЛІНДРИ»

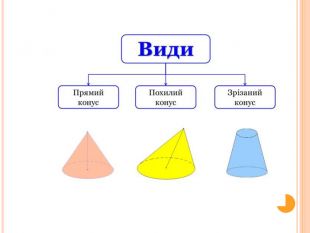
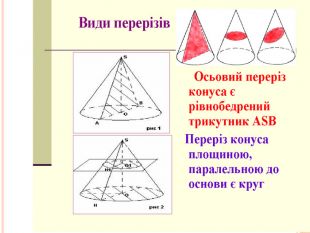
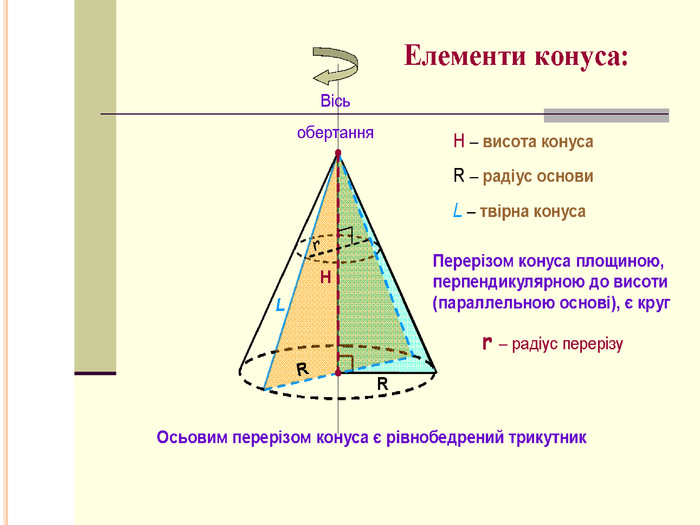
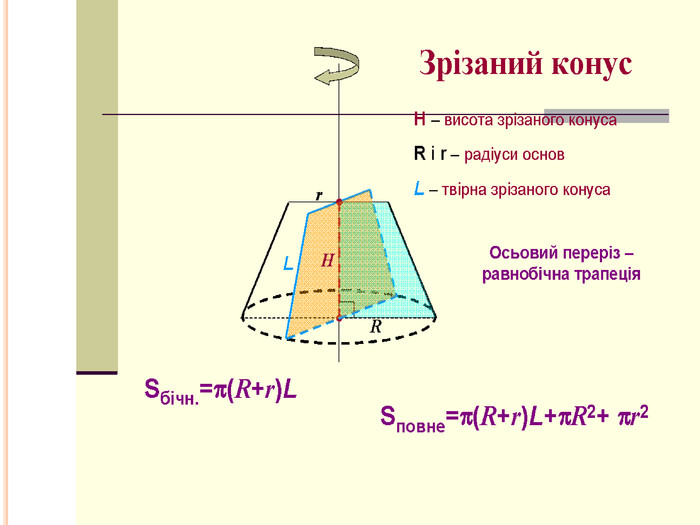
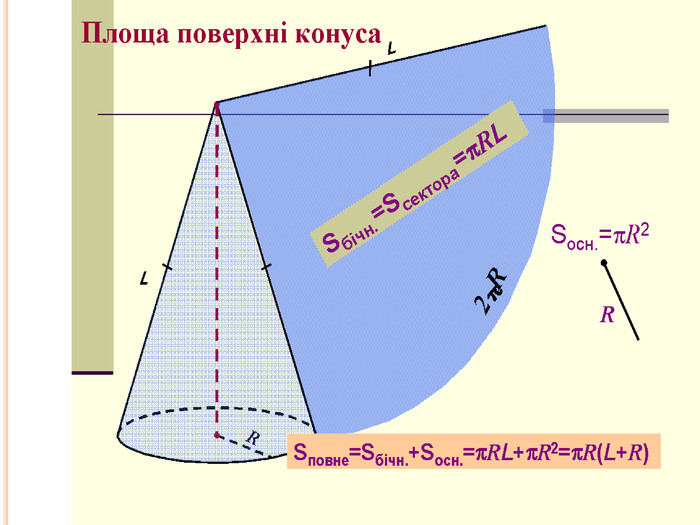
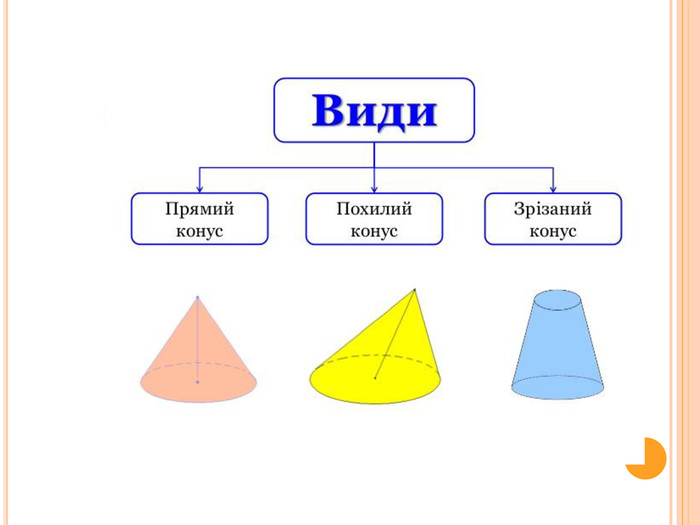
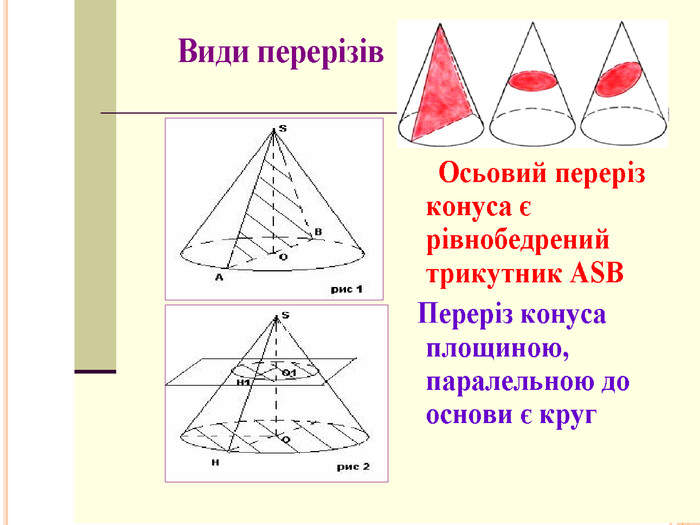
АПОЛЛОНІЙ І КОНУС Аполлоній Пергський давньогрецький математик і астроном. В залежності від взаємного розташування конуса і січної площини отримують три типи фігур: параболу, еліпс, гіперболу. У Евкліда немає поняття конічної поверхні, воно було введено Аполлонієм в його «Конічних перетинах». Ось що пише Аполлоній Пергський: «Якщо від будь-якої точки окружності кола, яка не знаходиться в одній площині з деякою точкою, проводити прямі, що з'єднують цю точку з колом, і при нерухомості точки переміщати пряму по колу, повертаючи її туди, звідки почався рух, то поверхню описану, я називаю конічною поверхнею, нерухому ж точку - її вершиною, а віссю - пряму, проведену через цю точку і центр кола»

ТАКОЖ ПРО ЦИЛІНДР ЗГАДУВАВ І ЙОГАНН КЕПЛЕР У ХVІ СТОЛІТТІ ДОСЛІДЖУЮЧИ ІДЕАЛЬНУ ФОРМУ ВИННИХ БОЧОК

Дослідники кулі та сфери.

ЗАВДАННЯ ГРУПИ: зібрати основні відомості про тіла обертання - кулю та сферу; з’ясувати де зустрічаються предмети, які мають форму кулі та сфери в повсякденному житті.

Історична довідка Куля походить від грецького слова (σφαίρας). Сфера походить від грецького слова «сфайра» , яке перекладається як «м’яч».

Куля – тіло, утворене обертанням круга навколо його діаметра. Куля та сфера Поверхня кулі називається сферою або кульовою поверхнею.

Основні поняття Куля Радіуси кулі Центр кулі Сфера Діаметр кулі Центр сфери Радіуси сфери

Формула для знаходження

Кульові форми в архітектурі, дизайні та флористиці Світлові ліхтарики

Кульові форми в природі Валун Моєраки сферичної форми Кульові блискавки

Кульові форми в сфері розваг Гелеві кульки

Кульові форми, вирощені та виготовлені людиною

Кульові форми в спорті Футбол Волейбол Баскетбол Гандбол Теніс

Кульові форми у Всесвіті Водно-гелієві кулі Сонячної системи: Сонце, Юпітер, Сатурн, Уран, Нептун Сонячна система Метеорити

Кульові форми та МИ

КОНУС

ЗАВДАННЯ ГРУПИ: зібрати основні відомості про тіло обертання – конус; з’ясувати де зустрічаються предмети, які мають форму конуса в повсякденному житті.

ЯЛИНКОВА ШИШКА З ГРЕЦЬКОЇ ОЗНАЧАЄ СЛОВО "КОНОС" . ТОМУ ТІЛА ТАКОЇ ФОРМИ ОТРИМАЛИ НАЗВУ КОНУС. КОНУС - ТРИВИМІРНА ФІГУРА, УТВОРЕНА ПРЯМОКУТНИМ ТРИКУТНИКОМ, ЩО ОБЕРТАЄТЬСЯ НАВКОЛО ОДНОГО З КАТЕТІВ.

ЧОМУ ВІДРА НА ПОЖЕЖНИХ ЩИТАХ РОБЛЯТЬ КОНІЧНОЇ ФОРМИ? Звичай робити пожежні відра конічними пішов з флоту. Під час пожежі треба швидко опустити відро прив'язане до кінця канату за борт і набрати води. Якщо дно у відра буде плоским воно не відразу потоне. Згадайте як іноді важко набрати води з глибокої криниці. Воно вперто не хоче тонути. З конічним дном цього не відбувається. Але все-таки пожежні відра роблять у вигляді конусів з інших причин. Річ у тім, що такими відрами зручніше черпати пісок з пожежного ящика (адже вогонь гасять не тільки водою, але і піском). Щоб зачерпнути пісок, треба взятися однією рукою за руків'я відра, а іншою - за його дно. З плоского днища звичайного відра рука в громіздкій пожежній рукавиці зісковзує. Набагато зручніше триматися за кінець конуса. До того ж конусоподібне відро легше занурювати в пожежну бочку з водою і виймати з неї вже наповненим. Крім того, взимку вода в бочці може перетворитись на лід. Кінчиком конуса пробити його легше. Пожежники також стверджують, що з відра-конуса воду можна виплеснути дальше і влучніше, ніж зі звичайного. 

КОНУС У НАУЦІ, ТЕХНІЦІ

КОНУС В АРХІТЕКТУРІ

КОНУС У ПРИРОДІ

ТА КОНУС У ЖИТТІ…

ЦИЛІНДР

ЗАВДАННЯ ГРУПИ:

Цилі́ндр від грецького κύλινδρος (kylindros)— вал, коток — геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.

ЦИЛІНДР Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.

ОСНОВНІ ПОНЯТТЯ

ВЛАСТИВОСТІ ЦИЛІНДРА 1) Основи циліндра рівні і паралельні. 2) Твірні циліндра паралельні і рівні. 3) Висота циліндра (відстань між площинами основ) дорівнює твірній.

ФОРМУЛИ C=2πr r r

ПЕРЕРІЗИ ЦИЛІНДРА ПЛОЩИНАМИ

ЦИЛІНДРИ НАВКОЛО НАС В архітектурі

ЦИЛІНДРИ НАВКОЛО НАС У техніці, промисловості та побуті

ЦИЛІНДРИ НАВКОЛО НАС У природі також маємо циліндричні форми

ЦИЛІНДРИ НАВКОЛО НАС У садівництві Господарські товари У малярній справі Канцелярське приладдя

ЦИЛІНДРИ НАВКОЛО НАС У харчовій промисловості

ЦИЛІНДРИ НАВКОЛО НАС У мистецтві У модельному бізнесі Циліндри фокусника Чоловічі та жіночі головні убори

У науці ЦИЛІНДРИ НАВКОЛО НАС У спорті

ЦИЛІНДРИ НАВКОЛО НАС У фармакології та медицині

ЦИЛІНДРИ НАВКОЛО НАС

ПРАКТИКИ «Не достатньо мати лише добрий розум, головне – це раціонально застосувати його» Рене Декарт.

ЗАВДАННЯ ГРУПИ: скласти задачі з прикладним змістом на застосування тіл обертання.

ЗАДАЧА №1 Скільки потрібно квадратних сантиметрів шкіри, щоб зробити покришку для волейбольного м’яча? (На шви і обрізки додати 5% матеріалу).

Басейн для дітей ЗАДАЧА №2 Визначіть: Якої площі ділянку потрібно виділити під басейн? Скільки квадратних метрів плитки потрібно для облицювання басейну всередині? 2м 1м

ЗАДАЧА №3 Для фарбування ялинкової іграшки в формі кулі діаметром 4см потрібно 60г фарби. Скільки фарби потрібно для фарбування іграшки діаметром 8 см?

ЗАДАЧА №4 Садівнику необхідно постригти кущ так, щоб він отримав форму конуса, при цьому твірна куща повинна бути 500 см і кущ повинен бути нахиленим під кутом 60 градусів. Яким повинен бути радіус основи куща?

ЗАДАЧА №5 З листа заліза вирішено зробити відро у формі конуса з діаметром основи 40см і висотою 60см. Скільки потрібно заліза? (Припуск заліза на шов – 0,6см.)

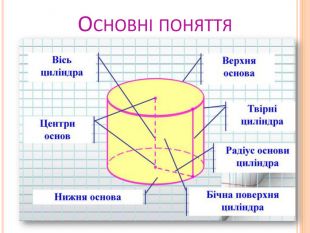
ЗАДАЧА №6 Бруски на нашому спортивному майданчику складаються з 6 труб, які мають форму циліндрів. На чотирьох підпорках висотою 3 м та діаметром 4 см, дві перекладини довжиною 1.55 м та діаметром 9 см. Скільки потрібно фарби, щоб оновити спортивне обладнання, якщо на 1 м2 потрібно 150 г фарби?

Без математики, зокрема геометрії, люди не могли б будувати, створювати, вимірювати та розв’язувати більшість практичних задач, які виникають щодня в повсякденному житті.

Розв’язування практичних задач запропонованих групою Практики.

Підготовка до ЗНО

3) ВСТАНОВІТЬ ВІДПОВІДНІСТЬ МІЖ ГЕОМЕТРИЧНИМ ТІЛОМ ТА ПЛОЩЕЮ ЙОГО ПОВНОЇ ПОВЕРХНІ

Домашнє завдання: Підручник Математика 11 клас, Мерзляк 2019 рік. Повторити п.19-21. Розв’язати задачі групи практики №2,№4,№5,№6.

Дякуємо за увагу!