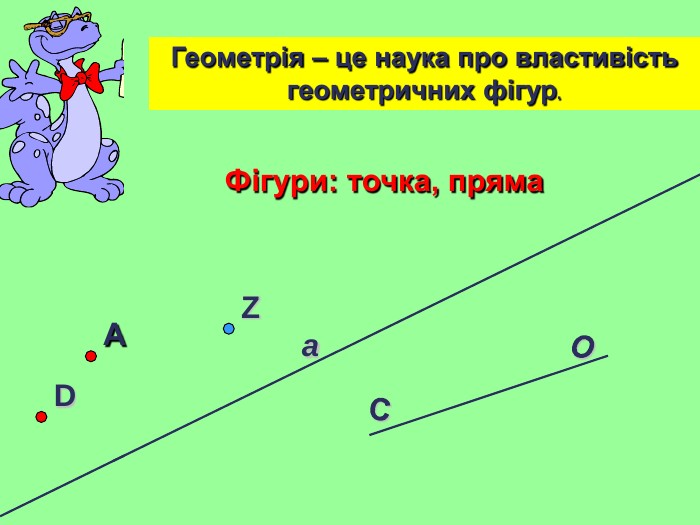
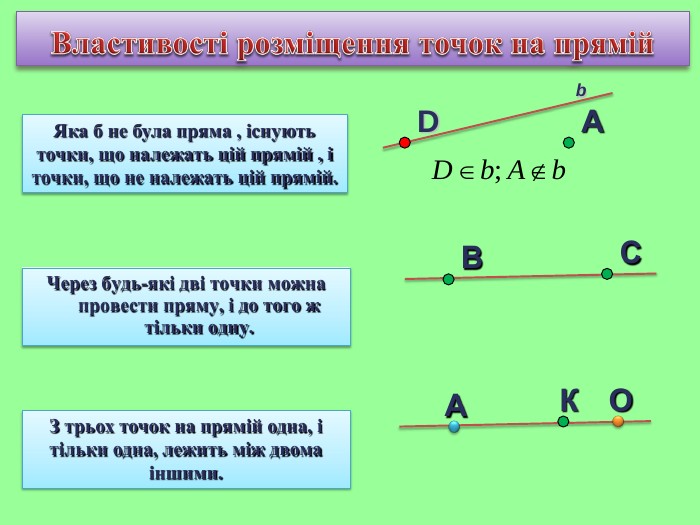
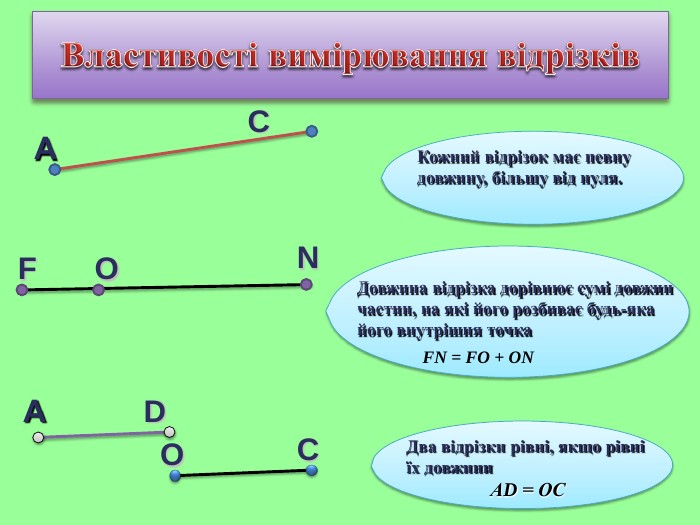
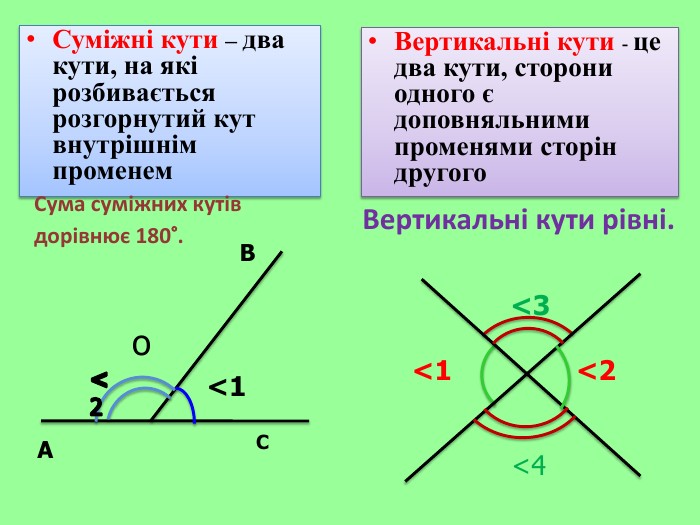
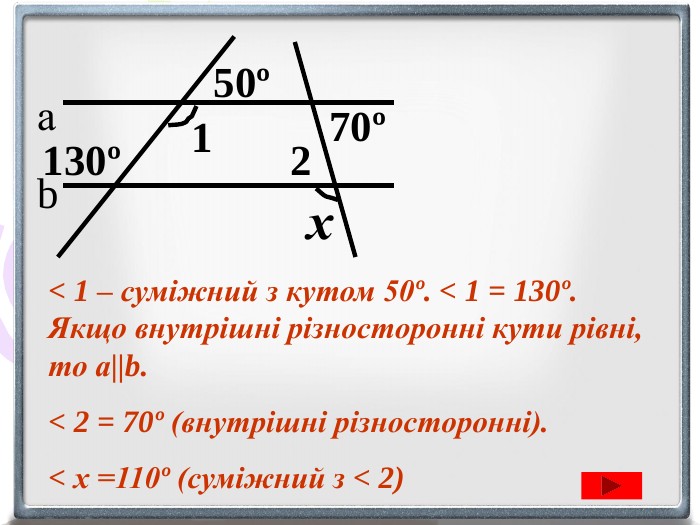
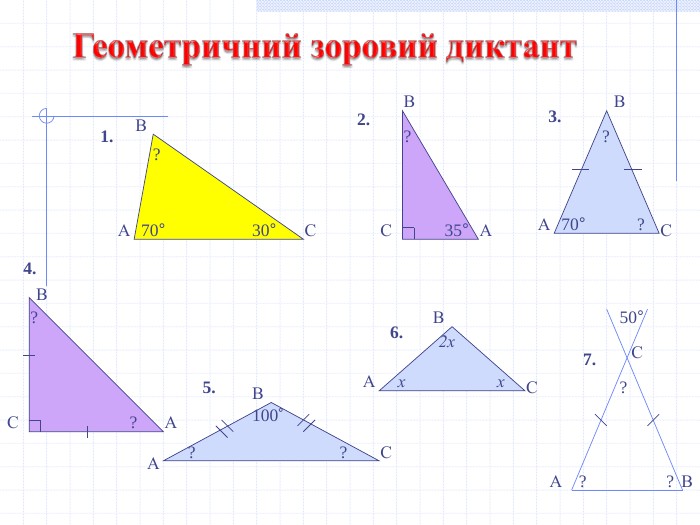
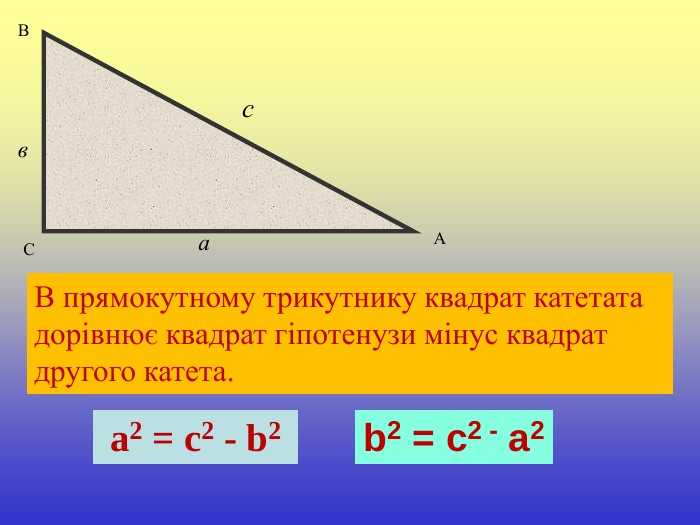
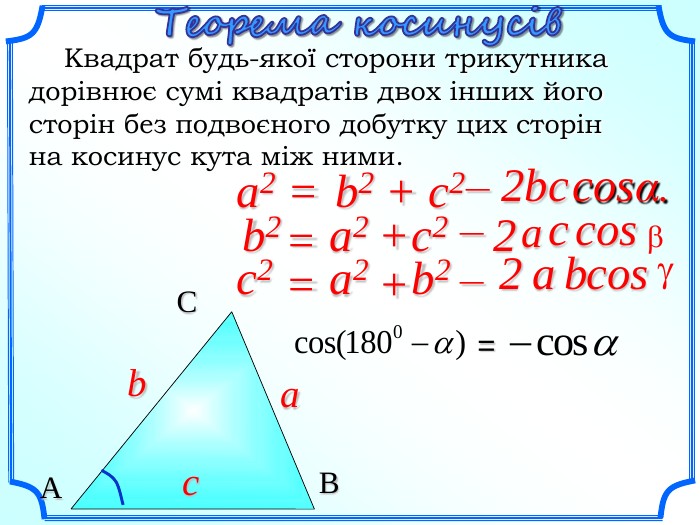
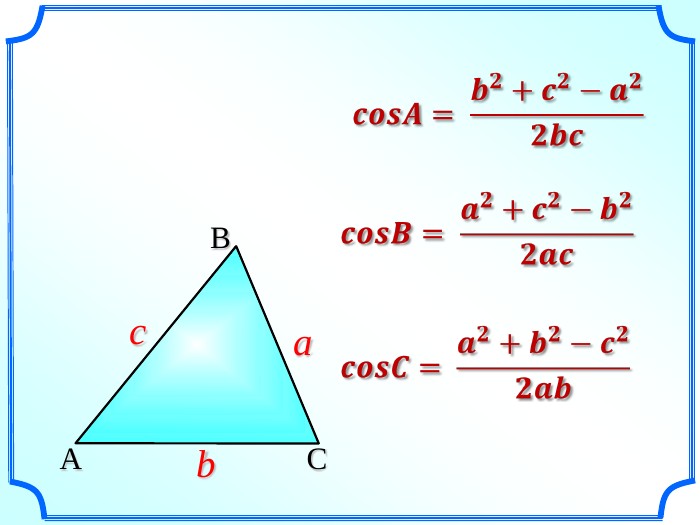
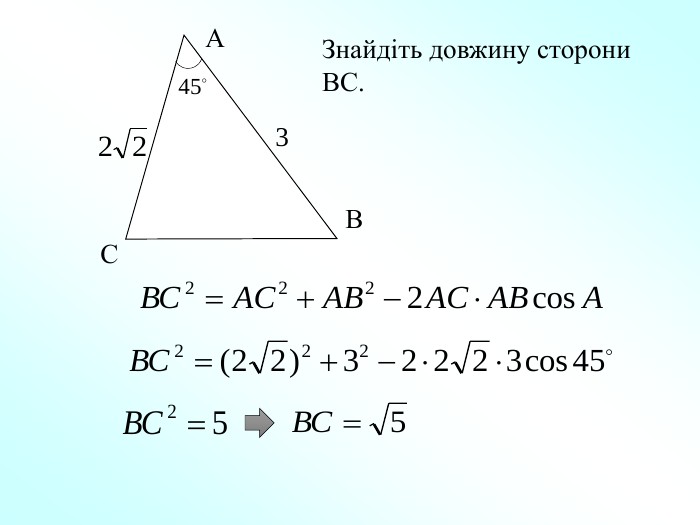
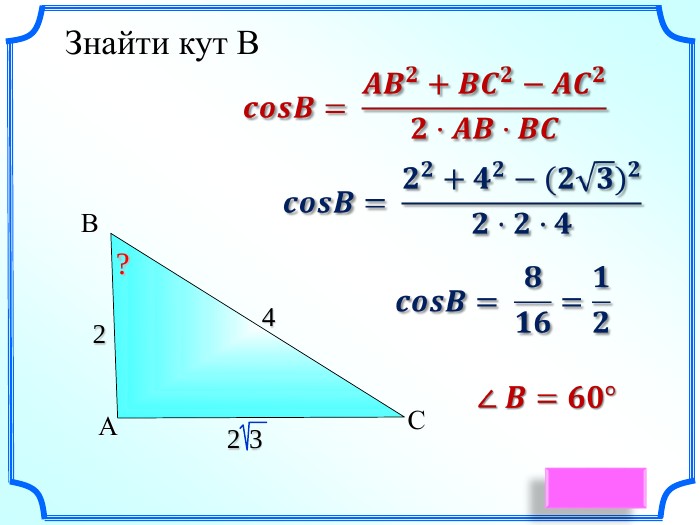
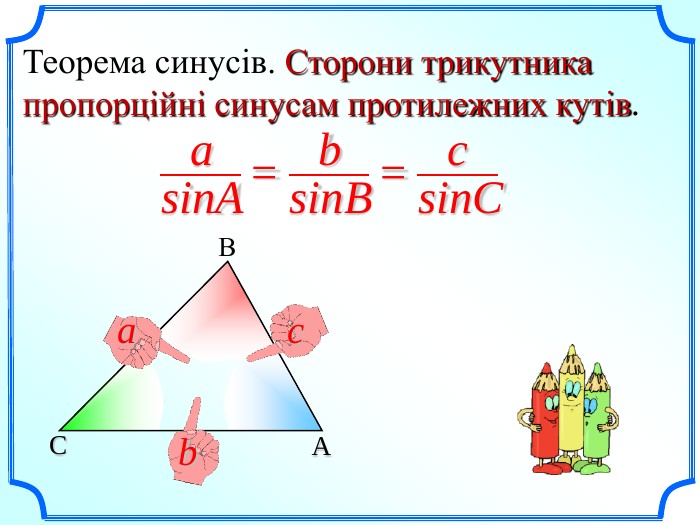
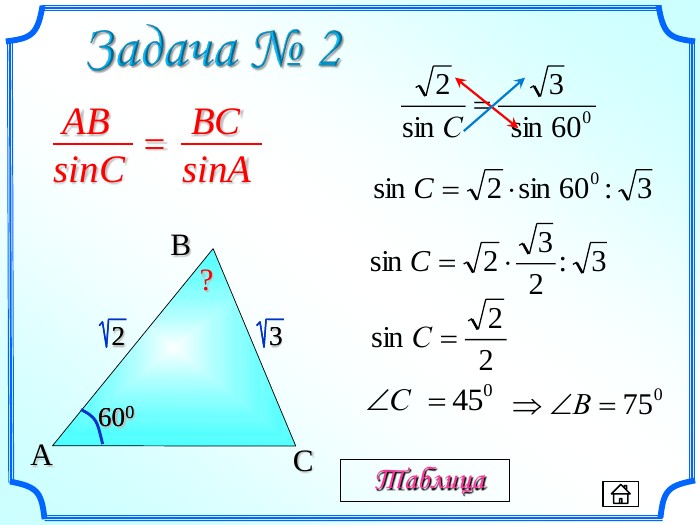
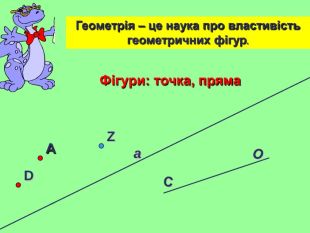
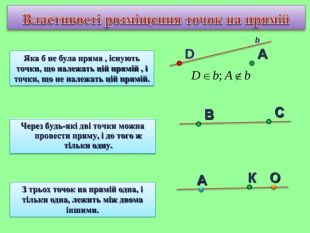
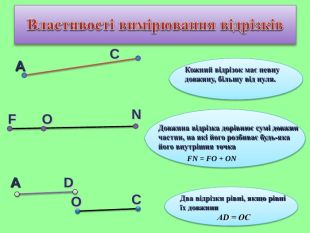
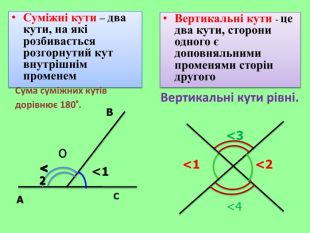
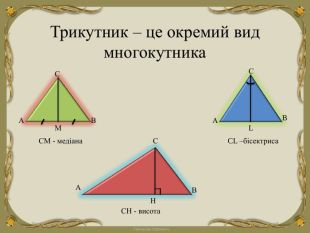
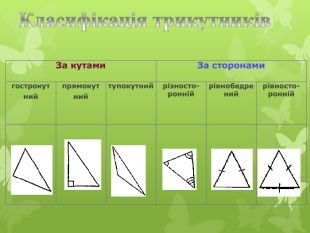
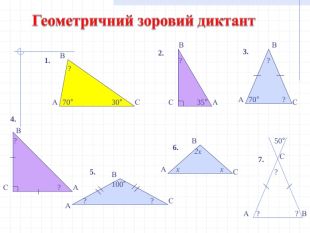
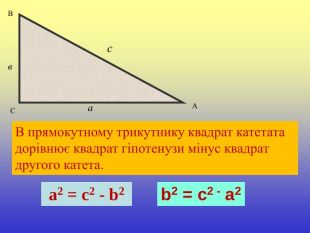
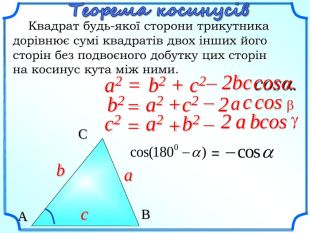
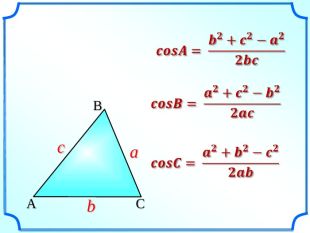
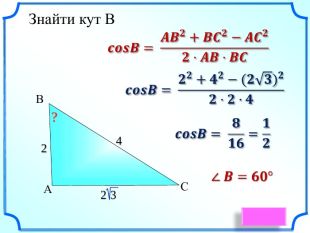
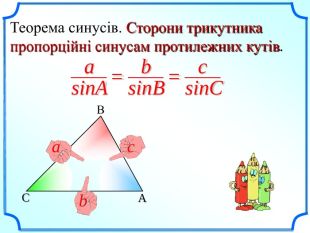
Презентація уроку "Повторення опорних фактів курсу планіметрії."

* * 7 вересня Класна робота

Система опорних фактів курсу планіметрії.

Мета уроку: Провести логічне узагальнення і систематизацію по вивченню і упорядкуванню навчального матеріалу з теми „Система опорних фактів курсу планіметрії”, що дозволить учням повторити матеріал теми у цілому та підготуватися до вивчення стеріометрії Формування навичок, застосування набутих знань до розв’язування вправ. Ознайомити учнів з різними способами розв’язування задач. Розвивати логічне мислення, вміння систематизувати, робити висновки, виховання свідомого навчання. Виховувати інтерес до навчання, дбати про активне сприймання.

Геометрія – це наука про властивість геометричних фігур. Фігури: точка, пряма А a D Z O C

Через будь-які дві точки можна провести пряму, і до того ж тільки одну. Яка б не була пряма , існують точки, що належать цій прямій , і точки, що не належать цій прямій. D А b С В З трьох точок на прямій одна, і тільки одна, лежить між двома іншими. А К О

F N А C Довжина відрізка дорівнює сумі довжин частин, на які його розбиває будь-яка його внутрішня точка FN = FO + ON Кожний відрізок має певну довжину, більшу від нуля. А C O Два відрізки рівні, якщо рівні їх довжини АD = ОС O D

Суміжні кути – два кути, на які розбивається розгорнутий кут внутрішнім променем о А В С <1 Вертикальні кути - це два кути, сторони одного є доповняльними променями сторін другого <1 <2 <3 <4 Вертикальні кути рівні. Сума суміжних кутів дорівнює 180°.

С А В Д Знайти: О Задача 1

С D К М А В О Знайти: Задача 2 1 2 3 5 4 6

А В С Порівняти та Задача 3

Якщо при перетині двох прями січною то ці прямі параллельні. Внутрішні різносторонні кути рівні Відповідні кути рівні оосОднторонні Односторонні в сумі 180°

с 1 а 3 2 b 4 5 6 7 <2 = 130є (вертикальний з даним); <1 = 50є (суміжний з даним); <3 = 50є (суміжний з даним); <4 = 130є (як відповідні кути); <7 = <4 = 130є (вертикальні); <5 = <3 = 50є (внутрішні різносторонні); <5 = <6 = 50є (вертикальні)

а b х 1 < 1 – суміжний з кутом 50є. < 1 = 130є. Якщо внутрішні різносторонні кути рівні, то а||b. < 2 = 70є (внутрішні різносторонні). < х =110є (суміжний з < 2) 2

Трикутники (опорні факти)

Трикутник – це окремий вид многокутника С А В М СМ - медіана С L А B CL –бісектриса С А В Н СН - висота

За кутами За сторонами гострокут­ ний прямокут­ ний тупокутний різносто-ронній рівнобедрений рівносто-ронній

1.Сума кутів трикутника дорівнює 180˚ ∠ А+ ∠ B+ ∠ C=180˚ 2. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним. ∠ BAK= ∠ ACB + ∠ ABC B C A K Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи. A C M B

А 1. В С ? А С В ? 2. 3. С А В ? ? 4. 5. 6. 7. ? ? ? ? х х 2х ? ? ? А А А А В В В В С С С С

Усі три медіани трикутника перетинаються в одній точці, яка ділить кожну з них у відношенні 2:1 рахуючи від вершини трикутника. BN/NK=2/1 B M K A N C Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні і дорівнює її половині. KL=ЅAB

Формулювання теореми Піфагора (алгебраїчне формулювання) a2 + b2 = c2 В прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. a b c

В прямокутному трикутнику квадрат катетата дорівнює квадрат гіпотенузи мінус квадрат другого катета. с в а А В С a2 = c2 - b2 b2 = c2 - a2

У прямокутній трапеції АВСД з основами АД і ВС, кут А – прямий, АВ = 4дм. З вершини С до основи АД проведений перпендикуляр СК, КД = 3дм, Знайдіть СД. Дано: АВСД – трапеция, <А =900 АВ = 4 дм. СК АД , КД = 3 дм. Знайти: СД.

Оскільки АВСД трапеція: АД//ВС, АВ//СК, АВ = СК = 4дм. Розглянемо ∆СДК, <К = 90°. CD2=KD2=KD2+CK2 За теоремою Піфагора: CD2= ; CD= =√25=5 (дм)

a2 = B a A C c b Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших його сторін без подвоєного добутку цих сторін на косинус кута між ними. b2 + c2 – 2bc cosα. b2 = a2 + c2 – 2 a c cos  c2 = a2 + b2 – 2 a b cos  =

A C B a b c

1.ВИЗНАЧТЕ ВИД ТРИКУТНИКА ІЗ СТОРОНАМИ 5, 6 ,7 см. > 2. ВИЗНАЧТЕ ВИД ТРИКУТНИКА ІЗ СТОРОНАМИ 2, 3, 4 см. > aІ> bІ+cІ трикутник тупокутний. aІ= bІ+cІ трикутник прямокутний aІ< bІ+cІ трикутник гострокутний трикутник гострокутний трикутник тупокутний.

Знайдіть довжину сторони ВС. А С В 3

4 С А В ? Знайти кут В 2 2 3

C В A a sinA b sinB = = c sinC a b c Теорема синусів. Сторони трикутника пропорційні синусам протилежних кутів.

де R – радіус кола, описаного навколо ∆ АВС

AB sinC BC sinA = C A B 600 600 ? 2 3 3 2 Таблица

домашнє завдання: Переглянути презентацію і записати приклади в зошити. Виконати завдання з презентації