Презентація "Узагальнення і систематизація навчального матеріалу з теми "Похідна"

Похідна. Узагальнення і систематизація навчального матеріалу Учитель математики МЗОПШ «Привилегия» Абрамова Валентин Вікторівна

Тема. Похідна

Похідна це. Похідної функції f(х) у точці х0 називають число, до якого прямує  відношення приросту функції до приросту її аргументу х коли х, прямує до нуля.

Згадуємо вивчене: Таблиця похідних

Функцію, яка має похідну у точці х0, називають дифференційовною у цій точці. Знаходження похідної функції f називають дифференціюванням функції. Приклади:х’=1;С’=0;(х2)’=2х; (хn)’=nхn-1 (х3)’=3х2;

Правила обчислення похідних. Похідна суми дорівнює сумі похідних : (f+g)'=f'+g' Похідна добутка :(f·g)'=f'g+fg'

Правила обчислення похідних Похідна частки: Похідна степеневої функції:

І. Завдання на знаходження похідної ступеня з цілим показником

1. Обчислити похідну Використовуємо формулу степеневої функції(хn)’=nхn-1 Розвязування: 𝒚′=−𝟓𝟒𝒙𝟒+𝟑𝒙𝟐−𝟐𝒙+𝟏𝟏′= −𝟓𝟒∗𝟒𝒙𝟒−𝟏+𝟑∗𝟐𝒙𝟐−𝟏−𝟐+𝟎==−𝟓𝒙𝟑+𝟔𝒙−𝟐  

2. Знайти похідну функції у точці х0 = -21) Знаходимо похідну (дивись попередній приклад)𝒚′=−𝟓𝟒𝒙𝟒+𝟑𝒙𝟐−𝟐𝒙+𝟏𝟏′= −𝟓𝟒∗𝟒𝒙𝟒−𝟏+𝟑∗𝟐𝒙𝟐−𝟏−𝟐+𝟎==−𝟓𝒙𝟑+𝟔𝒙−𝟐𝟐)  Потім подставляємо замість х значення −𝟐 та обчислюємо𝒚′−𝟐=−𝟓∗−𝟐𝟑+𝟔∗−𝟐−𝟐=−𝟐𝟔  

ІІЗавдання на використання похідних суми, різниці, добутку та частки функцій

3. Знайти похідну функції Використовуємо правило – похідної частки𝑦′=(4−3𝑥𝑥+2)’ = 4−3𝑥′𝑥+2−(𝑥+2)′(4−3𝑥)(𝑥+2)2==−3𝑥+2−(4−3𝑥)(𝑥+2)2=−3𝑥−6−4+3𝑥(𝑥+2)2=−10(𝑥+2)2 

4. Подібним чином знаходимо похідну добутку функцій          𝑦′=4𝑥−7′𝟖+𝟔𝐱+(4x-7)(8+6x)’= = 4(8+6x)+6(4x-7) = 48+24x+24x- 42 =48x+6 

ІІІЗавдання намеханічний та геометричний зміст похідної

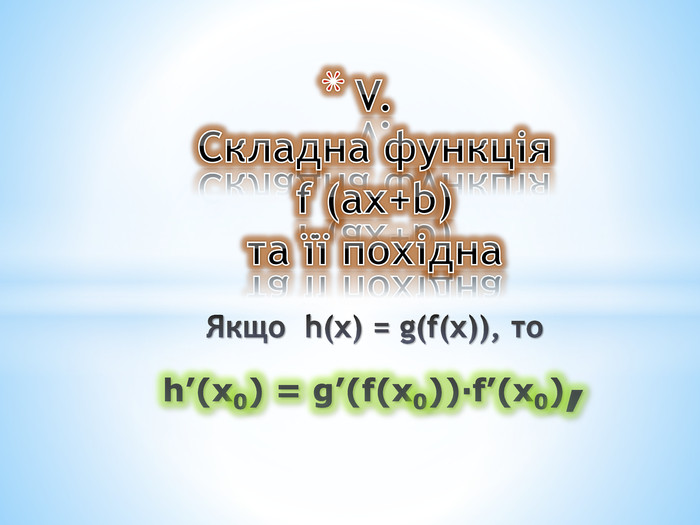
5. Матеріальна точка рухається по прямій так, що відстань S до неї від довільної точки А цієї прямої змінюється по закону S= 0,5t2-3t +2 (м), де t – час руху у секундах. 1) Через який час з початку руху швидкість матеріальної точки буде дорівнювати 15 м/с?2) Обчислити швидкість точки через 6 секунд з початку руху. 3) Через скільки секунд з початку руху точка зупиниться?

Розв’язання S= 0,5t2-3t +2 1) Через який час з початку руху швидкість матеріальної точки буде дорівнювати 15 м/с?Потрібно знайти швидкість! Швидкість – це похідна закону руху v=S’(t)=t-3=15 Розв ’ язуємо рівняння та знаходимо: t=18 Відповідь : Через 18 секунд з початку руху швидкість точки буде дорівнювати 15 м/с Механічний зміст похідної  полягає у тому, що  , 

Розв’язання S= 0,5t2-3t +2 2) Обчислити швидкість точки через 6 секунд з початку руху. Швидкість – це похідна закону руху v=S’(t)=t-3 Яка вона буде у момент t0=6? Подставляємо в формулу швидкості t0 : v=S’(t)=t-3=6-3=3 Розв ’ язуємо рівняння та знаходимо: v=3 м/с. Відповідь : Через 6 секунд з початку руху швидкість точки буде дорівнювати 3 м/с Механічний зміст похідної  полягає у тому, що ,

Розв’язання: S= 0,5t2-3t +2 3) Через скільки секунд з початку руху точка зупиниться?Якщо точка зупинилася, значить швидкість v=0 Потрібно знайти швидкість! Швидкість – це похідна закону руху v=S’(t)=t-3 та прирівняти 0!!!v=t-3=0 Розв ’ язуємо рівняння та знаходимо t =3 с. Відповідь : Через 3 секунд з початку руху швидкість точки буде дорівнювати 0 м/с Механічний зміст похідної полягаю у тому, що  , 

6. Знайти кутовий коэфіцієнт дотичної, проведеної до графіку функції f(х)=3х3+2х-5 у точці з абсцисою х=2. Геометричний зміст похідної   є кутовий коефіцієнт дотичної, який дорівнює тангенсу кута наклону дотичної з додатним напрямом осі абсцис: k=tg α = f’(x0 ) Значить для рішення мы знаходимо похідну та обчисляємо її значення у точці х=2 F’(x)=9х2+2 F’(x)=9*22+2=38 Отже k=38

Ми згадали, що : k=tg α = f’(x0 ) Знаходимо похідну та потім її дорівнюємо -5, обчислюємо та отримуємо f’(x)=4-6х, 4-6х=-5, 4+5=6х 6х=9 х=1,5 Відповідь: кутовий коэфіцієнт дотичної у точці x0 =1,5 дорівнює -57. Дана функція f(х)=5+4х-3х2 . Знайдіть координати точки ії графику, у якій кутовий коэфіцієнт дотичної до нього дорівнює -5.

ІVЗнаходження похідних тригонометричних функцій

Похідні тригонометричних функцій

8. Знайдіть похідну функції f(х)=2х2+sin x. F’(x)=4x +cos x (похідна суми дорівнює сумі похідних!)9. Знайдіть похідну функції f(х)=2х2 + tg x. F’(x)=4x +𝟏с𝒐𝒔𝟐𝒙10. Знайдіть значення похідної функції f(х)= tg х-2sin x при х=-∏/4. F’(x)=𝟏с𝒐𝒔𝟐𝒙 - 2cos x F’(-π𝟒)= 𝟏с𝒐𝒔𝟐(−π𝟒) −𝟐𝒄𝒐𝒔 −π𝟒==2-𝟐 Відповідь: При х=-∏/4 похідна дорівнює 2-𝟐  

V. Складна функція f (ax+b) та її похідна. Якщо h(x) = g(f(x)), то h’(x0) = g’(f(x0))·f’(x0),

Використання формули похідної складної функціїОбчислить: 11. 𝐹𝑥=(5𝑥−3)3 Рішення: Спочатку визначаємо похідну зовнішньої степеневої функції (5𝑥−3)3, а потім домножаємо на похідну внутрішньої функції (5х-3) 𝐹′(𝑥)=[5𝑥−3)3′=3∗(5𝑥−3)25𝑥−3′=5∗3∗(5𝑥−3)2=15∗(5𝑥−3)2 12. 𝐹𝑥= 5(5𝑥)3=(5𝑥35) Рішення𝐹′𝑥=35∗5(5𝑥2)∗5=35(5𝑥)2 

Будьте наполегливі, і все у вас вийде!