Презентація «Як розв’язувати текстові задачі»
Про матеріал
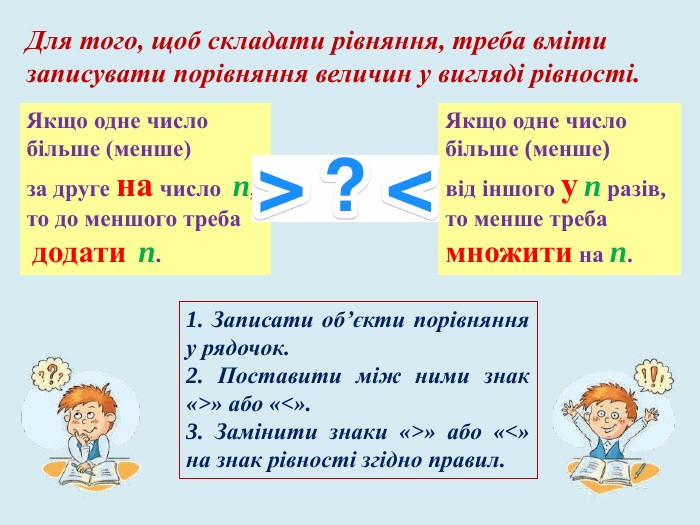
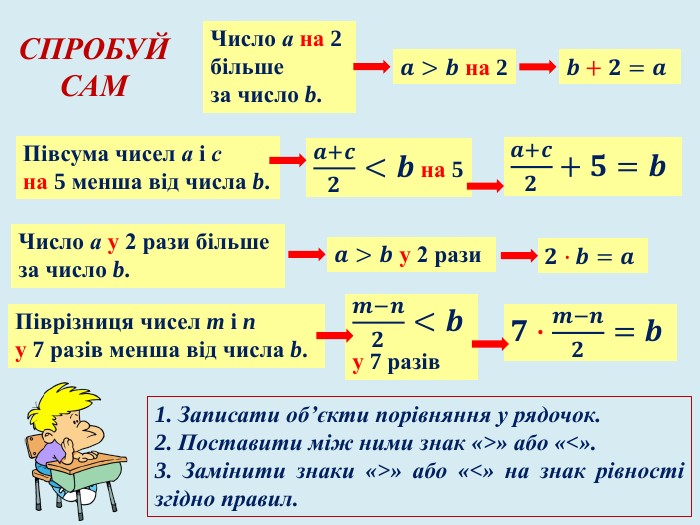
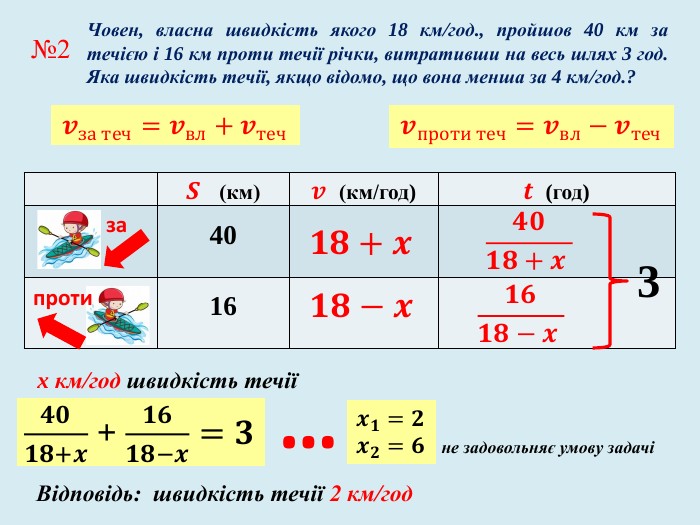
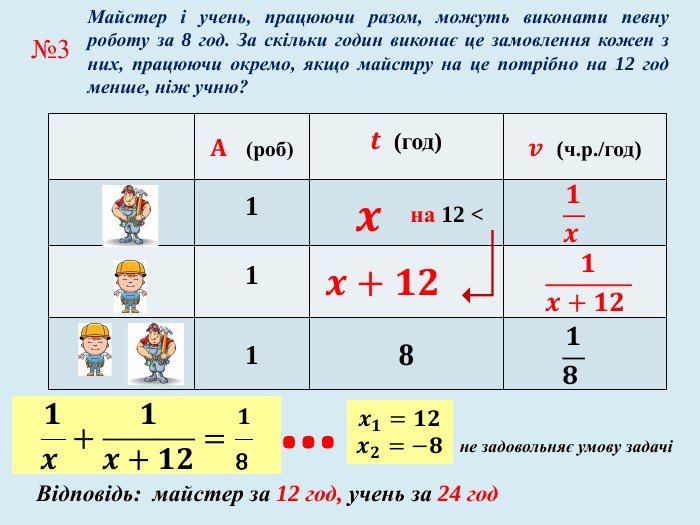
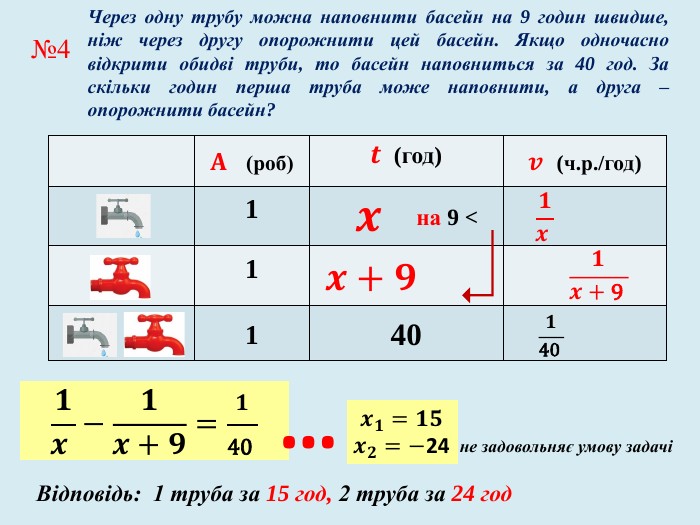
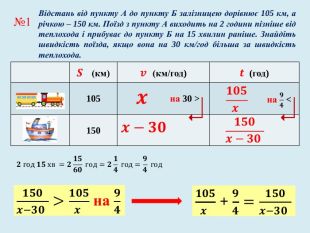
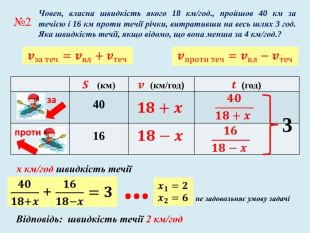
Задачі на спільну роботу та на рух мають багато спільного у математичній структурі: обидва типи задач містять три пропорційні величини, два об’єкти, але вони описують різні процеси: перші описують процес спільної праці двох об’єктів, а інші спільний рух двох тіл. Математична структура цих типів задач містить характеристики кожного з двох об’єктів, та характеристики їх спільної частини.
У презентації «Як розв’язувати текстові задачі» для учнів 8 класу. розглянуто правила складання рівнянь та приклади задач на рух та сумісну роботу.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку