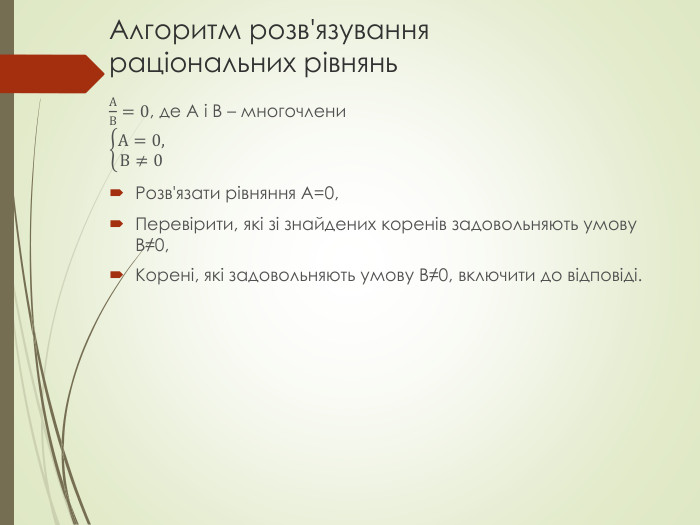
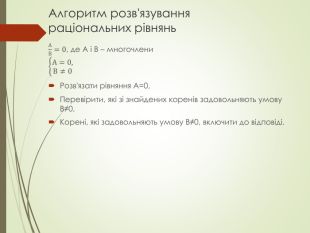
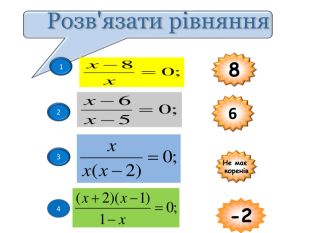
Презентація з теми "Раціональні рівняння. Розв'язування задач за допомогою раціональних рівнянь"
Про матеріал
Презентацію можна використати для пояснення нового матеріалу та для відпрацювання вмінь розв'язувати раціональні рівняння та задачі Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку