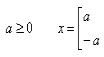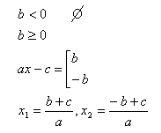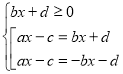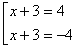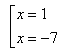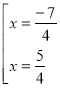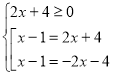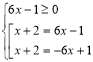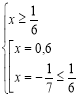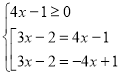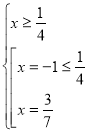«Найпростіші лінійні рівняння, що містять знак модуля: |x| = a, |x - a| = b, |ax - c| = b, |ax - c| = bx + d»
Тема уроку: Найпростіші лінійні рівняння, що містять знак модуля: |x| = a, |x - a| = b, |ax - c| = b, |ax - c| = bx + d.
Мета уроку: навчити учнів розв’язувати найпростіші лінійні рівняння з модулями, використовуючи алгебраїчний та геометричний зміст модуля, враховуючи обмеження на ліву частину рівняння |ax - c| = bx + d; розвивати навчальні інтереси, здібності на основі розумових дій, формувати навички аналізу; виховувати пізнавальну активність учнів, активну позицію в навчанні і житті.
Хід уроку
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
ІІI. Мотивація навчальної діяльності.
Принцип, якого дотримуються в процесі узагальнення деяких, у тому числі і математичних, понять, називається перманентність. Це слово означає сталість, неперервність. Саме цим принципом ми користуємось на уроках, послідовно вивчаючи модуль та його властивості. Сьогодні ми навчимося розв’язувати лінійні рівняння, що містять модуль.
Тож епіграфом нашого уроку є такі слова:
Вся математика – це власне , одне велике
рівняння для інших наук.
Новаліс
ІV. Актуалізація опорних знань.
- Назвіть число, протилежне даному:
а) -1,2; б) 0; в) ![]() .
.
- Назвіть число, модуль якого дорівнює 3,9. Скільки існує таких чисел?
- Вкажіть на координатній прямій числа, модуль яких дорівнює 4.
- Як розташовані числа 2 і -2 відносно початку відліку на координатній прямій?
- Дати означення модуля, геометричний зміст модуля.
6. Чи правильно розкрито модуль ?
1. | x 4 + 3 | = x 4 + 3.
2. | 2 – | = + 2.
3. | x – 5 | = 5 – x, x > 5.
4. | x + 3 | = – x + 3, x < – 3.
5. | x 2 – 10x + 26 | = x 2 – 10x + 26.
Правильні відповіді:
1. Так. 2. Ні. 3. Ні. 4. Ні. 5. Так.
(Всі відповіді подаються дітьми з обґрунтуванням).
V. Сприймання навчального матеріалу.
Щоб краще зрозуміти, як розв’язуються найпростіші рівняння з модулем, звернемося до геометричного змісту модуля. Як відомо, вираз |a - b| означає відстань між точками a і b, а розв’язати рівняння |x| = a, означає знайти такі числа х відстань, від яких до початку координат дорівнює а:
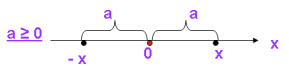
У рівнянні |x - a| = b - відстань між точками а і х дорівнює b:
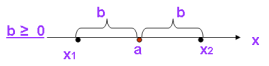
У рівнянні |аx - с| = b - відстань між точками ах і с дорівнює b:
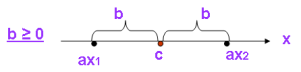
У рівнянні |аx - с| = bx + d, – відстань між точками ах і с дорівнює bx + d:
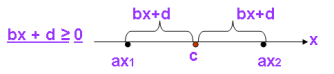
Очевидно, що рівняння мають корені лише тоді, коли вирази, які стоять у правій частині рівняння будуть невід’ємними.
З геометричної інтерпретації випливають такі алгоритми розв’язання:
|
|x| = a,
|
|x - a| = b
|
|ax - c| = b,
|
|ax - c| = bx + d
|
|
|
b ≥ 0
|
|
|
VI. Засвоєння навчального матеріалу.
1. Розв’яжіть рівняння. У відповідь запишіть суму коренів.
|
|x +3| = 4 -6 |
|1-2х| = 0 0.5 |
|- 4х - 1| = 6 - 0,5 |
|
|
|
|
|
|x -1| = 2х + 4 -1 |
|х+2| = 6х – 1 0,6 |
|3х - 2| = 4х - 1 3/7 |
|
|
|
|
Розв’яжемо декілька прикладів, використовуючи геометричний зміст модуля числа :
Приклад 1.![]()
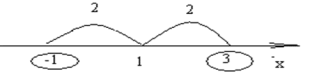 .
.
Відповідь: ![]() .
.
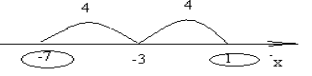
Приклад 2. ![]() .
.
Відповідь: ![]() .
.
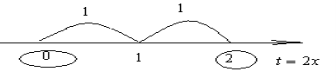 Приклад 3.
Приклад 3. ![]() .
.
![]()
Відповідь: ![]() .
.
Чи є ще якісь способи розв`язування лінійних рівнянь з модулем? Так! Інколи доцільно піднести ліву і праву частини рівняння з модулями до квадрату.
«Модуль полюбляє квадрат». Розглянемо декілька прикладів:
Приклад 4: |x – 1| = x +1
Розв’язання.
![]()
![]() .
.
Відповідь: ![]() .
.
Приклад 5: |4 – x| = |2x – 2|
Розв’язання.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
VІI. Підсумок уроку.
VIІI. Домашнє завдання.
Розв’яжіть рівняння.
-
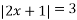 ;
;
-
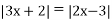 ;
;
-
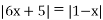 ;
;
-
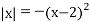 ;
;
-
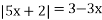 .
.


про публікацію авторської розробки
Додати розробку