Презентаційний матеріал до заняття "Найпростіші тригонометричні рівняння виду tg x = a".
Про матеріал
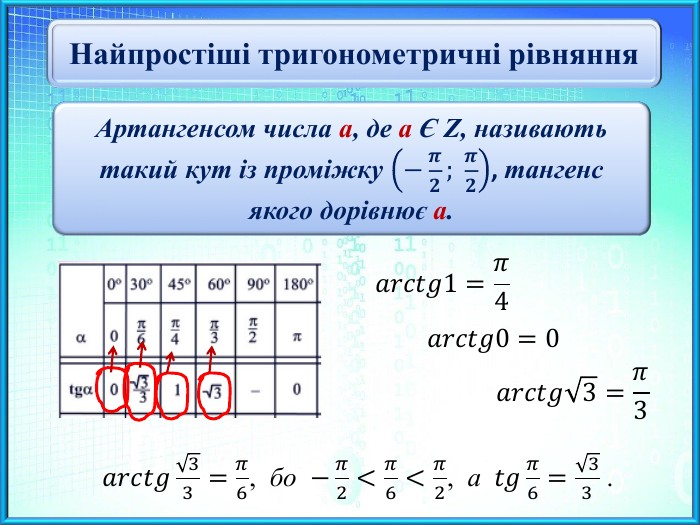
Презентаційний матеріал до заняття "Найпростіші рівняння виду tg x = a"
містить формули для знаходження коренів найпростіших тригонометричних рівнянь виду tg x = a та приклади розв’язання таких рівнянь. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку