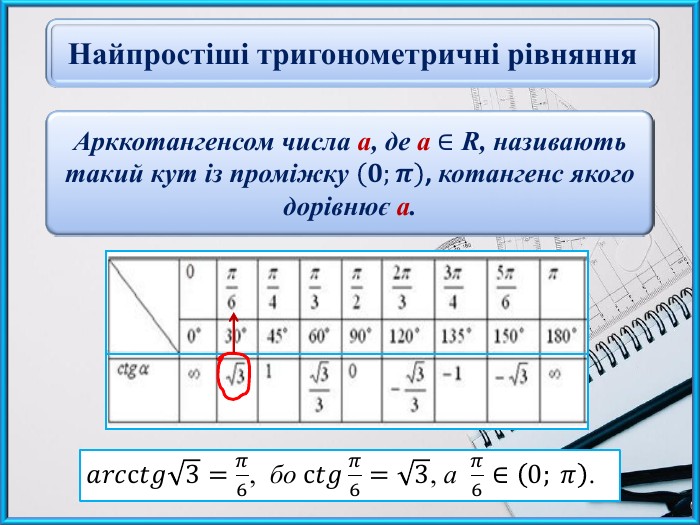
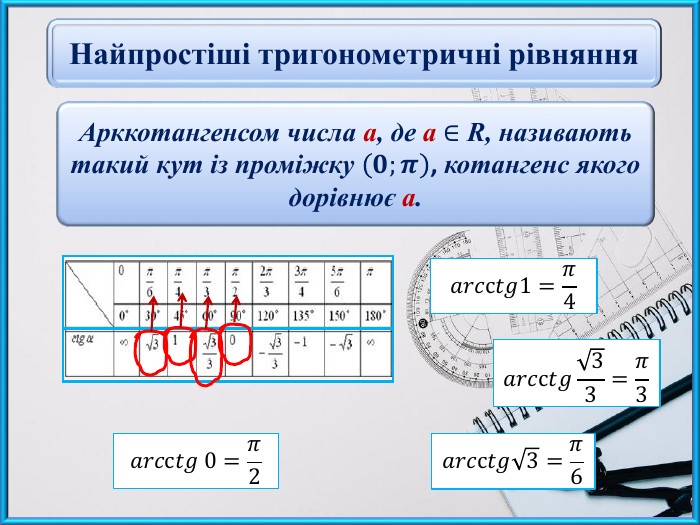
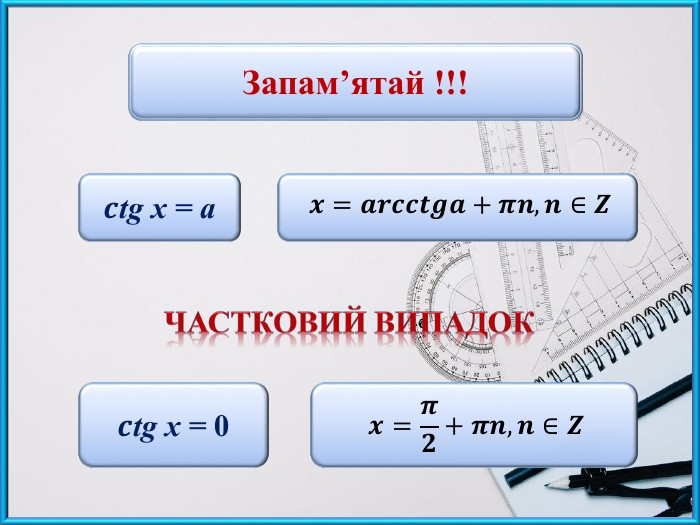
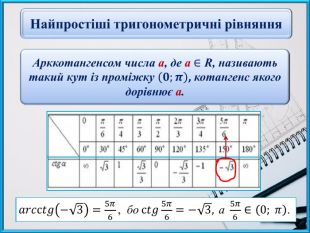
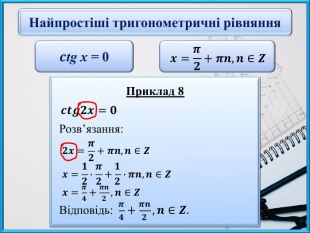
Презентаційний матеріал до заняття "Найпростіші тригонометричні рівняння виду сtg x = a".
Про матеріал
Презентаційний матеріал до заняття "Найпростіші тригонометричні рівняння виду сtg x = a". Мета. Сформувати вміння розв’язувати найпростіші тригонометричні рівняння. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку