Прикладні задачі з теми "Застосування теореми синусів і теореми косинусів"

Галина Дудар

ТЗОШ І-ІІІ ст. №19,

м Тенопіль

Складаємо інтелект -карту з теми «Теорема синусів. Теорема косинусів. Розв’язування трикутників». Прикладні задачі

Завершуючи тему , що стосується відомих теорем геометрії, а саме, теореми синусів і теореми косинусів, варто навести лад із вивченим матеріалом. У цьому нам допомагають майнд-карт (інтелект -карти), або кластери. Пропоную скласти свою інтелект-карту з опрацьованих тем. Вона допоможе пригадати головне, зорієнтуватися, як застосовувати вивчений матеріал при розв’язуванні задач. Адже згадані теореми мають величезне значення і широке застосування у математиці, і не тільки в математиці. Ця інтелект-карта складена на ХMind ZEN і доповнена у Paint/

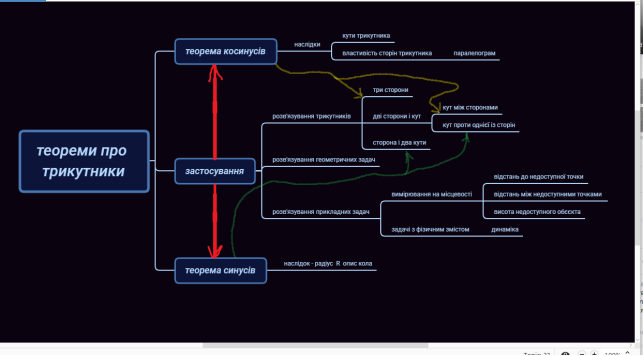
 Давайте разом  проведемо невеличку екскурсію у минуле великих теорем.

Починаючи з давніх часів і приблизно до XVII століття у тригонометрії розглядали виключно «розв’язування трикутників», тобто обчислення одних елементів трикутника (або многокутника, розбитого на трикутники0 за іншими елементами. Такі обчислення виникали з потреб астрономії, мореплавства, геодезії, архітектури.

Теорема косинусів, по суті, була доведена, звісно, спочатку геометрично, ще у «Началах» Евкліда, а саме у 12-му і 13-му реченнях ІІ книги. У якій узагальнюється теорема Піфагора і виводяться формули , які виражають квадрат сторони, яка лежить проти гострого чи тупого кута трикутника. Це положення, доведене Евклідом, еквівалентне теоремі косинусів

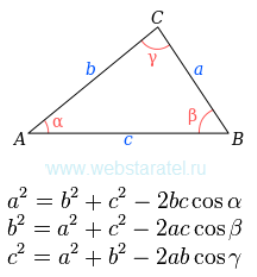
Сучасного вигляду теорема косинусів набуває приблизно у 1801 році у французького математика Лазара Карно (1753-18230). Ж.Л. Лагранж вивів у 1799 році теорему синусів з теореми косинусів. Інший французький математик, О. Коші, виводить теорему косинусів із теореми синусів у своєму «Курсі аналізу» у 1821 році.

Вчені Індії. Як і учені країн ісламу у ІХ-Х століттях, зводили розв’язування будь-яких трикутників до розв’язування прямокутних трикутників. Тому у них не було потреби у теоремі косинусів. Вони її не знали. Цю теорему довів лише у одинадцятому столітті уродженець Хорезму видатний астроном і математик ал-Біруні.

 Разом із співвідношенням

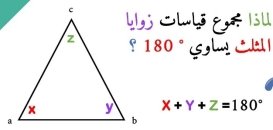
теорема синусів

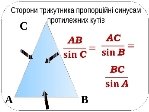
давала можливість розв’язувати будь-який трикутник. Теоремою синусів користувалися починаючи з XVI століття європейські математики.

 ( за матеріалами Г. И. Глейзер . История математики в школе. 7-8 класс. М., Просвещение, 1982).

А тепер розглянемо кілька прикладних задач на застосування теореми синусів та теореми косинусів.▫

Задача 1.

На кришці парового циліндра діаметром 350 мм треба просвердлити 8 отворів для болтів. Знайдіть відстані між центрами отворів, якщо ці центри повинні бути від країв кришки на відстані 50мм.

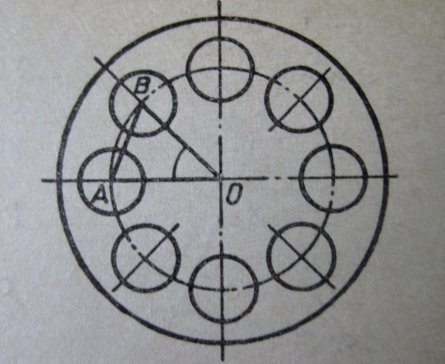
Розв’язання

1. АО=ВО=125 мм  (за умовою задачі).
2. ∟АОВ=360◦ :8=45◦
3. За теоремою косинусів АВ² =АО²  +ВО² –2АО∙ВО cosАОВ.
4. АВ² ≈9153 мм² , АВ≈95, 6 мм^2.

Відповідь. 95,6 мм² .

Задача 2

З двох міст А і В  виїжджають одночасно два потяги відповідно за напрямами АD і ВЕ, які перетинаються у місті С під кутом 60◦. Обидва поїзди рухаються рівномірно зі швидкостями відповідно 20 км/год і 30км/год. За скільки годин з моменту їх відправлення відстань між ними буде дорівнювати початковій, якщо АС=50 км, ВС=40 км?

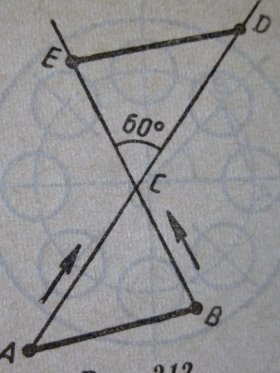
Розв’язання

Нехай t- час який потрібно знайти. Тоді за умовою задачі АD=20t, ВЕ=30t,СD=20t-50, СЕ=30t-40.

З трикутника DЕС за теоремою косинусів : DE² = (20t-50)² + (30t-40)² – (20t-50)(30t-40²  cos60◦.

З трикутника АВС за теоремою косинусів АВ² =50² +40² -2∙50∙40cos60◦=2100.

Враховуючи, що АВ=DE, знаходимо час t. t=3 год.

Відповідь. Через 3 години.

Задача 3

Силу, що дорівнює 23 Н треба розкласти на дві складові, кути яких з напрямом заданої сили дорівнюють відповідно 47◦ і 54◦. Знайти величину кожної із цих сил.

Розв’язання

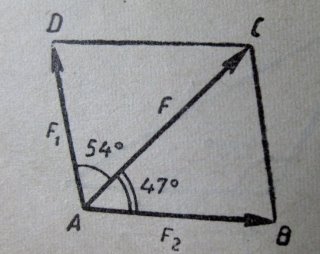
∟DAC=54◦, ∟СAB=47◦, тому ∟ADC=79◦. За теоремою синусів

= = .Звідси F₁ ≈17 H, F₂ =19 Н.

Задача 4

Дорога на гору піднімається двома виступами у вигляді ламаної лінії, перший виступ утворює з горизонтом кут 30◦, а другий - 65◦. А пряма , яка з’єднує її з основою гори, нахилена до горизонту під кутом 60◦. Довжина виступу дорівнює 1км. Знайти висоту гори.

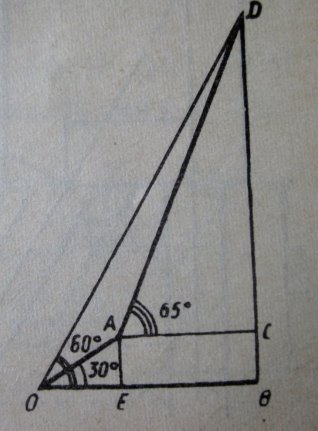
Розв’язання

За умовою ∟АОЕ=30◦, ∟DОЕ=60◦, тому ∟DOA=30◦, ∟ODB=30◦.

∟DAC=60◦, тому ∟ADC=25◦ і ∟ADO=5◦.З трикутника OAD за теоремою синусів = . Отже, маємо: АD=≈5,74 км. З трикутника ACD знаходимо DC= AD∙sin65◦≈5,2 км, СВ=АЕ=0,5ОА≈0,5 м. Висота гори DB≈5,7 км.

Відповідь. 5,7 км

Задача 5

Судно йде точно на схід із швидкістю 12 вузлів. О 13 год 10 хв азимут напряму на маяк дорівнював 70◦, а о 13 год 40 хв він становив 20◦. На якій відстані від судна знаходився маяк під час другого показу? Відомо, що один морський вузол відповідає 1 морській милі за годину.

Розв’язання

Нехай маяк знаходиться у точці М.

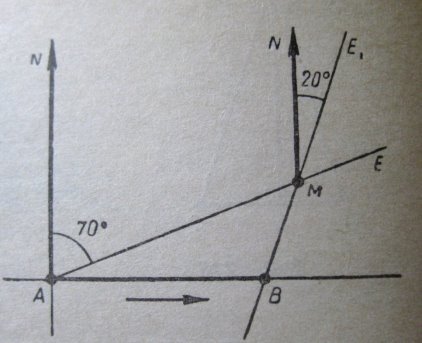
Оскільки судно прямує точно на схід, то воно рухається по променю АВ  (кут NAB-гострий). О 13год 10 хв судно знаходилось у точці А (∟NAM=∟NME=70◦).

Якщо о 13год 40хв азимут напряму на маяк становив 20◦, то в цей момент воно знаходилось у точці В (∟NME₁ =20◦).

За 0,5 год судно пройшло відстань АВ, яка дорівнює 6 миль. Нехай ВМ=х. Кут АМВ=50◦, а кут МАВ=20◦.

За теоремою синусів

= або =  Звідси маємо. Що х≈ 2,7 морських миль.

Відповідь. 2. 7 морських миль.

Ще кілька цікавих задач для самостійного розв’язання

Задача 6

Залізний стержень довжина якого х см треба зігнути під кутом так, щоб відстань між його кінцями була у см. Де повинна знаходитись  точка згину? За яких умов задача матиме розв’язки?

Задача 7

З гелікоптера , який знаходиться на висоті 1650 м, було помічено колону автівок. Початок колони видно під кутом пониження  70 градусів, а кінець під кутом 65 градусів. Знайдіть довжину колони.

Задача 8

На матеріальну точку діють сили 35 Н і 85 Н під кутом 70 градусів. Знайдіть рівнодійну цих сил і кут, який утворює вона із більшою із даних сил.

Задача 9

Із спостережного пункту помічено літак, який пролітає над вежею. Висота якої 80м. Пряма, яка з’єднує спостережний пункт і верхівку вежі, утворює з горизонтальною площиною кут 25 градусів. На якій висоті пролітає літак?

Задача 10

Три населених пункти А, В, С розміщені так, що дороги які їх з’єднують утворюють трикутник. Відстань між А і В становить 24 км, між В і С – 36 км . Дороги , які ведуть з міста В у міста А і С утворюють кут 60 градусів. Яка відстань між містами А і С? Де потрібно розмістити АЗС, щоб відстань з усіх міст до неї була однаковою?  Результати округлити до сотих.