Проєкт "Математика - наука прикладна"

 

 

 

 

Л.І. Трохименко

 

 

 

 

Трохименко Любов Іллівна – учитель математики, учитель вищої кваліфікаційної категорії

 

 

 

 

 

       Автор пропонує проект

«Математика – наука прикладна»

 з теми: «Послідовності і прогресії»

      У роботі представлена проективна діяльність, яка сприяє активному залученню учнів до продуктивної творчої праці.

       Робота може бути корисною для вчителів математики середніх шкіл.

 

 

 

 

 

 

 

 

 

Передмова

     Вивчення математики в усіх відношення дає надзвичайно багато. Математика і властивий їй стиль мислення – невід’ємні елементи справді глибоко й цілісного світогляду та загальної культури сучасної людини.

     Реалізація прикладної спрямованості – важливий напрямок у викладанні математики. Тому на учня слід дивитися як на особистість з безліччю ступенів свободи і інтелекту.

     У своїй роботі автор мав на меті ефективне навчання, яке спонукає в учнів бажання та потребу в завданнях і викликає інтерес до предмета, допомагає розвитку здібностей кожного учня, розвиває вміння та навички застосовувати отримані знання на практиці, а також самостійно здобувати ці знання.

     Проект мав на меті розвиток інтелектуальних здібностей дітей таких як розвиток дослідницьких якостей, поновлення своїх знань про навколишній світ.

     В ньому значна увага приділена розвитку творчих здібностей, розвитку вміння працювати самостійно.

     Вирішальне значення має звернення до прикладів із життя і навколишньої дійсності.

     Історизм у викладанні математики та її прикладна спрямованість пов’язані. Цей зв'язок очевидний, оскільки більшість понять класичної математики, що потрапили до шкільного курсу, зобов’язані своїм виникненням практичним потребам людини.

     Звернення до конкретних фактів з історії розвитку  математики  та вивчення математичних об’єктів  розвиває  практичний зміст математичних понять, пробуджує  пізнавальний інтерес учнів до науки.

      Враховуючи сучасні суспільні умови, завдання реалізації прикладної спрямованості шкільного курсу математики є актуальним.

 

 

 

 

 

 

 

 

Проект

«Математика  - наука прикладна»

9 клас

Любов Трохименко, учителька математики, Світлана Пуха, учителька математики, Валентина Шевченко, заступник директора з навчально-виховної роботи ЗОШ І-ІІІ ступенів, Катерина Магар,учениця 11 класу,  с. Суха Маячка, Полтавської обл.

     Використання проектної технології в навчально-виховному процесі сприятиме підвищенню рівня якості освіти та підготовки молоді до життя й виходу на ринок праці.

     За резутатами досліджень різних міжнародних організацій, учні з пострадянських  держав відрізняються від своїх зарубіжних однолітків великим обсягом знань і водночас неспроможністю застосовувати їх у реальному житті. Використання в навчальному процесі методу проектів дає змогу подолати ці розбіжності, навчати дітей самостійно здобувати нові знання та застосовувати їх на практиці. Адже теоретичні знання – це база, на основі якої формуються вміння та навички.

 

                                            Мозок, добре впорядкований,

                                        вартий більше, ніж добре наповнений.

 М. Монтень

 

Керівники проекту: Трохименко Л.І.,Пуха С.Г.,Шевченко В.В., Магар К.І.

Учасники проекту: учні 9-го класу.

Тип проекту: навчальний.

 

І. Актуальність проекту.

Основними у діяльності школи на сучасному етапі має стати девіз:

       «Допоможи мені це зробити самому».

       Ідеально відповідає цій потребі проективна  діяльність, бо вона  сприяє активному залученню учнів до продуктивної творчої  праці.

       Актуальним залишається питання підвищення рівня навчальних  досягнень  школярів з математики.

      Даний проект сприяє формуванню креативної  компетентності  учнів, створює оптимальні умови для їх самореалізації, розкриття  творчого потенціалу та допомагає в реалізації життєвих планів особистості школяра.

 

ІІ. Мета і завдання проекту.

• Активізувати пізнавальну діяльність учнів.
• Сприяти розвитку інтелектуальних і творчих здібностей.
• Розвивати навички мислення.
• Прищеплювати навички роботи з додатковими джерелами інформації, вміння самостійно орієнтуватися в інформаційному просторі.
• Формувати навички дослідницької діяльності на основі спільної праці учнів.
• Розвивати в учнів уміння оцінювати та самооцінювати набуті знання.
• Формувати вміння генерувати ідеї, працювати в групі.
• Формувати в учнів уміння застосовувати набуті знання в нестандартних умовах.

   

 

ІІІ. Механізм реалізації проекту.

• Постановка проблеми.
• Визначення теми та мети проекту.
• Ознайомлення учнів із суттю проекту та основними етапами його реалізації.
• Робота з інформаційними ресурсами.

 

 

ІV. Орієнтовні напрямки реалізації проекту.

Учні об’єднуються у групи з урахуванням бажань, здібностей, нахилів,способу мислення.

Задання для групи «Мандрівники в минуле»

• З’ясування історії виникнення прогресій.
• Робота з додатковими джерелами інформації.
• Розв’язування прикладних задач.
• Робота в групах.

Завдання для групи «Обчислювачі  сум»

• Допомога групі «Мандрівники в минуле» знайти суму 64 членів геометричної прогресії, перший член  якої  дорівнює 1,а знаменник – 2, тобто кількість зерен дещо іншим способом, ніж у шкільному підручнику.
• Виведення формули суми перших членів,геометричної прогресії в загальному вигляді.
• Знаходження суми.
• З інформаційних джерел: формули для знаходження сум членів послідовності степенів натуральних чисел.
• Самостійна робота в тестовій формі (два варіанти).

Завдання для групи «Прогресії»

• Випуск газети «Найдавніша прогресія».
• Пошук та підготовка цікавих матеріалів про прогресії (написання рефератів).
• Оголошення конкурсу «Склади кросворд».

Завдання для групи «Дослідники»

• Виготовлення наочності з  теми «Прогресії і послідовності».
• Створення презентації «Послідовність Фібоначчі».
• Застосування формули суми

.+.

• Повідомлення «У світі цікавого».

 

V. Очікувані результати

• Активізація пізнавальної діяльності учнів.
• Підвищення інтересу до вивчення математики.
• Розвиток інтелектуальних і творчих здібностей учнів.
• Розвиток навичок дослідницької діяльності.
• Формування навичок самостійної роботи з додатковими джерелами інформації.
• Формування вміння працювати в групі, генерувати ідеї.
• Аналіз та систематизація тих знань, які здобуті на уроках або з додаткової літератури.

 

VI. Оцінка та самооцінка проекту

              Поміркуйте над тим, що вам вдалося найкраще. Критично оцініть свою роботу. Дайте відповіді на такі запитання.

• Чого ви разом з однокласниками навчилися?
• Яких умінь і навичок набули, працюючи над проектом?
• У чому полягають переваги роботи у групі?
• Як ви можете вдосконалити свої навички й уміння для кращого вирішення проблем?

 

VII. Представлення результатів діяльності учасників

• Написання рефератів.
• Випуск газети «Найдавніша прогресія»
• Конкурс «Склади кросфорд»
• Наочність до теми «Прогресії і послідовність»
• Презентація «Послідовність Фібоначчі».

VIII. Сценарій проекту

Керівник проекту. Шановні гості!

Ми вітаємо вас і запрошуємо нас послухати. Ми отримали завдання знайти цікавий матеріал про прогресії і послідовності.

         Учень 1. Розповідають, що одного разу вчитель початкової школи, бажаючи зайняти клас на тривалий час самостійною роботою дав дітям «важке» завдання – обчислити суму всіх натуральних чисел від 1 до 100.

          Один з учнів в одну мить запропонував розв’язання.

           Це був Карл Фрідріх Гаусс.

           В  9 річному віці він знайшов спосіб для обчислення суми натуральних чисел до 100 включно.

           Він потім став одним з найвидатніших математиків світу.

            Пропоновані учителем числа були п’ятизначними і  становили арифметичну прогресію з тризначною різницею.

 Керівник проекту. Сьогодні 9 клас представляє прогресії і

послідовності.

Учень 2. Нам відома формула суми квадратів n перших

натуральних чисел.

Це не арифметична і не геометрична прогресія, але сума ця

може бути знайдена при допомозі формули суми арифметичної прогресії.

          Формула ця часто полегшує розв’язання задач. Вона була відома вже Архімеду.(ІІІ ст. до н.е.). Він нею користувався при розв’язуванні геометричних задач.

           Архімед (близько 287 – 212 р. до н. е.) у праці «Про число піщинок» уперше порівнював арифметичну та геометричну прогресії.

           Це справді захоплююче.

           Учень 3. Ми підготували цей проект разом із учителем математики за матеріалами підручника та рефератів, де зібрано наукову інформацію з додаткових джерел.

           Учні виконали розрахунки, пов’язані з прогресіями; вивчили історичні задачі, пов’язані з сумою прогресій; випустили газету «Найдавніша прогресія»; підготували слайди в комп’ютерному вигляді.

         Результатом нашої роботи став проект «Математика – наука прикладна».

         Керівник проекту. Як розв’язувати нестандартні задачі? На це запитання будуть відповідати дослідники та історики, теоретики та практики. Нестандартні задачі будуть презентувати керівники груп «Мандрівники в минуле», «Обчислювачі сум», «Прогресії», «Дослідники». Тож надаємо їм слово.

        Керівник групи  «Мандрівники в минуле».

           Наша група отримала завдання з’ясувати історію виникнення прогресій. Тому ми здійснили подорож у минуле та дізналися про таке.

       У знайдених під час розкопок папірусах, яким налічується понад 2000 років, виявлені задачі на прогресії. Це наштовхує на думку про те, що прогресії люди знали ще з давніх часів і використовували їх для розв’язання прикладних задач.

       З давніх давен відомі задачі та легенди, в результаті розв’язання яких з’являються числа-гіганти.

      Зрозуміло, що мова йде про задачі, пов’язані з геометричною прогресією (q 1).

     Одна з найбільш відомих легенд – легенда про винахідника шахів.

     Задача 1. Індійський принц Сідам(VІ ст.) запропонував винахіднику шахів таку винагороду, яку тільки той захоче.

     Винахідник попросив, щоб за першу клітинку шахової дошки йому дали одну пшеничну зернину, за другу – дві, за третю – чотири і т.д. за кожну наступну клітинку у два рази більше, ніж за попередню.

     Таку нагороду не можна було видати, оскільки кількість зернин становить: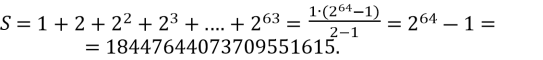

     Якщо таку кількість зернин рівномірно розсипати по всій земній поверхні, то утвориться шар пшениці товщиною 9 мм, в якому на 1

припадає 4,3 кг зерна.

    Підраховано, що кількість зернин, які б хотів отримати винахідник шахів, складає число, що приблизно становить 13,8 млрд. 40 – тонних вагонів.

    Ця задача вперше зустрічається у математика аль-Біруні (973-1050).

    Керівник проекту. Ідеться мова про задачі поставлені потребами практики. Над деякими такими задачами доводилось працювати роками. Ось як писав про свої пошуки розв’язку однієї задачі великий німецький математик Фрідріх Гаусс (1777-1855): «Протягом чотирьох років рідко проходив тиждень, коли б я не робив тієї або іншої спроби розв’язати цей вузол. Але всі намагання, всі зусилля були марні, і сумно я клав перо. А недавно…

Загадка розв’язалася із швидкістю блискавки… 

 І коли я викладу це питання, ніхто не зможе уявити собі, якого напруження коштувало мені це розв’язання».

Розв’язування прикладних задач

      Учень 1. Нами було з’ясовано, що геометрична прогресія застосовується в токарній справі, конструкторській справі, в архітектурі, фізиці, економіці, біології.

     Біологія

     Розглянемо задачу, пов’язану з використанням геометричної прогресії у біології.

     Задача 2.

     Деякі бактерії, вміщені в живильне середовище, діляться навпіл кожні дві години. Скільки бактерій в цьому випадку утвориться з однієї бактерії  через 10 год. ?

Розв’язання

    Описану в задачі ситуацію зафіксуємо за допомогою таблиці.

 

К-сть півгодин	0	1	2	3	4	…	20
К-сть бактерій	1	2				…

 

   Отже, матимемо:

(бактерій).

Робота в групах

       Керівник проекту. А тепер робота в групах з нестандартними завданнями.

       Знайти суму:

а) -100-99-98-97-…-1+1+2+…+100+101+102

Відповідь: 203

б) 1+2-3-4+5+6-7-8+9+10-11-12+13+14-…+301+302

Вказівка. Треба згрупувати по чотири доданки так, щоб у дужках сума дорівнювала 0.

в) 1+2+3+…+(n-1)+n.

Відповідь:

г) 2+4+6+…+2(n-1)+2n

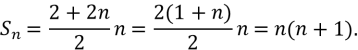
Відповідь:

      Знайти суму:

а)

б)

в)

г)+

Відповідь:

         Керівник проекту. В чому полягає раціональний прийом для обчислення таких сум?

     (Добуток дробів дорівнює їх різниці).

          Хотілося б, щоб ви не шукали одразу відповіді, а діставали їх завдяки особистим зусиллям. Як влучно зауважив відомий американський математик і педагог Д.Пойа, велике наукове відкриття дає розв’язання великої проблеми, але і в розв’язанні будь-якої задачі є крупинка відкриття.

         Розв’язання кожної задачі є не тільки відкриттям нового факту, а й задоволенням наукової допитливості, часто бажанням завбачити майбутнє.

       Керівник групи «Обчислювачі сум».

      Ми отримали таке завдання: допомогти групі «Мандрівники в минуле» знайти суму 64 членів геометричної прогресії, перший член якої дорівнює 1, а знаменник – 2, тобто кількість зерен, дещо іншим способом, ніж у шкільному підручнику:

   

   

.

   Аналогічно можна вивести формулу суми перших членів геометричної прогресії в загальному вигляді.

  Розглянемо приклади на обчислення суми.

      Приклад 1.

  Знайти суму

      Приклад 2.

Нехай – арифметична прогресія, її різниця – d,

Обчислити

Розв’язання 

=

=

 

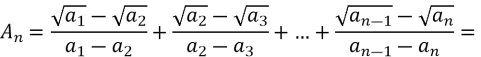
        Приклад 3

Знайти суму:

Розв’язання

 

=

=

Відповідь:

       З інформаційних джерел ми дізналися про суми однакових степенів послідовних членів арифметичної прогресії. Тепер нам добре відомі формули для знаходження сум членів послідовності степенів натуральних чисел, тобто:

;   (1)

; (2)

; (3)

;(4)

          Самостійна робота

в тестовій формі (два варіанти).

          Керівник групи «Прогресія»

         Учениця 1 Наше завдання полягало в тому щоб зібрати цікавий матеріал про прогресії. Підсумком нашої роботи став випуск газети «Найдавніша прогресія». Крім того, ми зібрали багатий матеріал про «Прогресії і середні», «Тотожності, цікаві й корисні»

        Ми оголосили конкурс «Склади кросворд». Найкращі з них ви зможете побачити в наступному випуску газети і спробуєте розгадати їх. Переможця буде визначено.

        Учениця 2

        Задача 3    Три числа, останнє з яких дорівнює 12, утворюють геометричну прогресію. Якщо замість 12 взяти 9, то три числа утворюють арифметичну прогресію. Знайти ці числа.

Розв’язання

       Нехай  - члени геометричної прогресії;

         - члени арифметичної прогресії.

     Скориставшись характеристичними властивостями геометричної та арифметичної прогресій, дістанемо систему рівнянь:

 

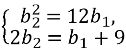
    Розв’язавши цю систему, дістанемо:

1)

2)

Відповідь:  1)27,18,9;  2)3;6;12.

Керівник групи  «Дослідники»

         Наша група отримала завдання з’ясувати чи існують інші послідовності, крім арифметичної і геометричної прогресії. Виявляється, що існують. 

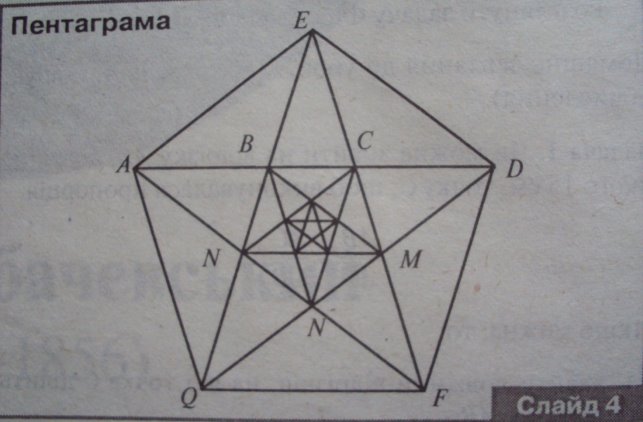
     По-перше, закономірностями краси є: пропорції, симетрії, визначні математичні криві, геометричні форми, дослідження «красивих» теорій. До так званих «красивих» теорій відноситься послідовність Фібоначчі. Ця теорія переповнена цікавим історичним змістом.

     По-друге, числа Фібоначчі виникли з добре відомої задачі про кроликів італійського математика Леонардо Пізанського (Фібоначчі)(1170-1250). Вони привернули увагу багатьох математиків. Теорія чисел Фібоначчі до цього часу залишається однією з найкрасивіших теорій елементарної математики.

      Задача Фібоначчі

      Скільки пар кроликів народиться за рік від однієї пари, якщо кожна пара дає щомісяця приплоду по одній парі, яка в свою чергу здатна до розмноження через один місяць, і якщо жодна пара не загине?

• На початку року маємо 1 пару кроликів, через 1 місяць їх буде –

2 пари, через два місяці – 3, через три – 5, потім через кожний місяць кролів буде відповідно 8,13,21,34,55,89,144,233 і, нарешті, 377 пар,а всього 986 пар.

     Розв’язання задачі привело до цікавої рекурентної числової послідовності:

    1,1,2,3,5,8,13,21,34,55,89,144,233,377,…,

+ Французький  математик Едуард Люка (1842-1891) назвав послідовності, члени яких утворюються за таким рекурентним законом, рядами, або послідовностями Фібоначчі, а їх члени – числами Фібоначчі. Числа Фібоначчі постають при розв’язуванні численних практичних і теоретичних задач і мають багато цікавих властивостей. Зокрема, суму n послідовних чисел Фібоначчі можна обчислити за формулою:

           У ХІІІ ст. італійський математик Леонардо Пізанський досліджував послідовність 1,1,2,3,5,8,13,21,…, кожний член якої починаючи з третього, дорівнює сумі двох попередніх членів. Кілька століть математики не могли знайти її n-й член. Тепер він відомий:

     

          Послідовність  Фібоначчі- Нарайани – одна з багатьох цікавих історичних задач, яка потребує тривалого дослідження.

         Числа Фібоначчі мають широке застосування у повсякденному житті.

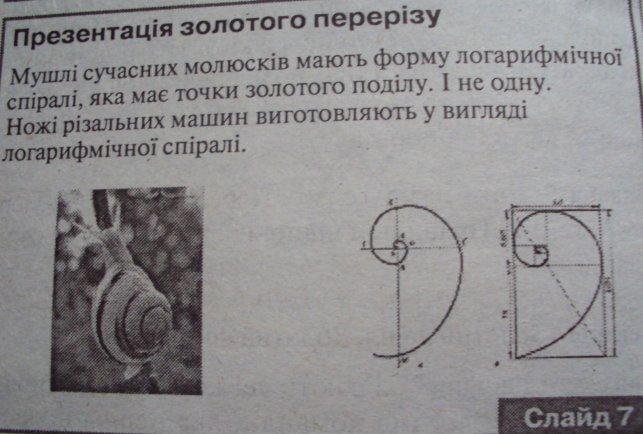
         З опрацьованих інформаційних джерел нам стало відомо, що є ще надзвичайно багато прикладів, у яких спостерігаються числа Фібоначчі та золота пропорція.

         До вашої уваги слайди підготовлені в комп’ютерному вигляді.

Учень

Розв’язати рівняння

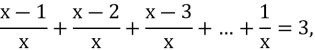
де - ціле додатне число.

Розв’язання

   Помножимо обидві частини цього рівняння на , маємо:

    (.

    Ліва частина цього рівняння – сума членів арифметичної прогресії, де

1 =

1 =

    Оскільки , то

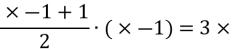
  Відповідь:

       Керівник проекту. Хто має які доповнення?

       Учень. Протягом тисячоліть поняття прогресії розвивалось і удосконалювалося. Цей процес триває і в наш час.

      Працюючи над рефератом мені стало відомо, що є й інші послідовності, які теж вважаються прогресіями. Назву деякі з них:

                                             гармонічна прогресія,

квадратична прогресія,

 логарифмічна прогресія,

                                            степенева прогресія,

                                            нескінченна прогресія.

       Слід зауважити, що деякі питання теорії розглянутих прогресій,наприклад, на питання про формулу суми членів кожної з них, не має певної відповіді: ці питання ще чекають на своє розв’язання.

      Керівник проекту. З рядом чисел Фібоначчі ви зустрінетесь в 10 класі при вивченні теми «Трикутник Паскаля».

         Формула суми квадратів натуральних чисел

+  знаходить застосування в різних питаннях математики.

        При вивченні теми «Первісна та інтеграл» в 11 класі у вступній бесіді буде запропоновано розв’язати таку задачу:

        Обчислити площу фігури, обмеженої параболою , віссю 0 та прямою .

       До обчислення площі заданої фігури не можна застосовувати формули, відомі для обчислення площі многокутників.

     Площу цієї фігури можна обчислити наближено. Щоб знайти наближене значення площі розглядуваної фігури необхідне знання формули

.+.

     Цю формулу ви матимете можливість застосовувати при обчисленні границь послідовностей, навчаючись у ВНЗ.

     Гадаю, що ви зрозуміли, що математичні задачі виникли у зв’язку з необхідністю виконувати розрахунки для будівельних робіт, під час збирання податей, розподілу майна, обміну й розподілу продуктів, вимірювання площ полів, об’ємів гребель і зерносховищ, організації великих караванів та ін.

      Потрібні наполегливість і самодисципліна, щоб у годину дозвілля добровільно вирушити в неспокійну подорож лабіринтами математичних задач.

    Є в математичних задачах особлива привабливість, яка поведе вас до нових логічних поворотів і перевалів. А народжений інтерес стане надійною аріадновою ниткою, яка вкаже правильний шлях і подарує особливу, не зрівнянну  ні з чим радість пізнання істини.

    «Якийсь математик сказав, - писав Л.М. Толстой, - що насолода не у відкритті істини, але в шуканні її».

    Вам,діти, бажаю знайти свій шлях у безмежний і чарівний світ математики, у цю стародавню і вічно молоду, «суху» і надзвичайно поетичну науку.

    Ви добре справилися з завданнями, а це говорить про те, що

 « … и будет собственных Ньютонов, и быстрых разумом Платонов украинская земля рождать».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література

1. Математика. Шкільний світ. №5(449), лютий 2008,ст.20.
2. В.А. Вишенський, М.Й. Ядренко. Вибрані математичні задачі. Вид. Об’єднання «Вища школа». К.: 1974, с.16.
3. Депман І.Я. За сторінками підручника математики.М.: Просвітництво, 1989.
4. Кочетов Е.С., Кочетова Е.С. Алгебра і елементарні функції. Часть І. –М.: Просвітництво,1974.
5. Математика. Шкільний світ. №7 (451), лютий 2008.
6. Я.І.Перельман «Цікава алгебра», видавництво «Наука», 1974 рік, ст.170.
7. У світі математики. Випуск 9. К. 1978, с.46.
8. Вейль Г. Симетрія. – М.: Наука,1968.
9. Волков Ю.І., Войналович Н.М. Елементи дискретної математики.

-         Кіровоград, 2000.

10.Воробйов Н.Н. Числа Фібоначчі. – М.:Наука, 1978.

11.Підоу Д. Геометрія і мистецтво. – М.: Мир,1979.

12.Журнал «Математика в школах України», березень  

      2009р.,№7(235),с.27