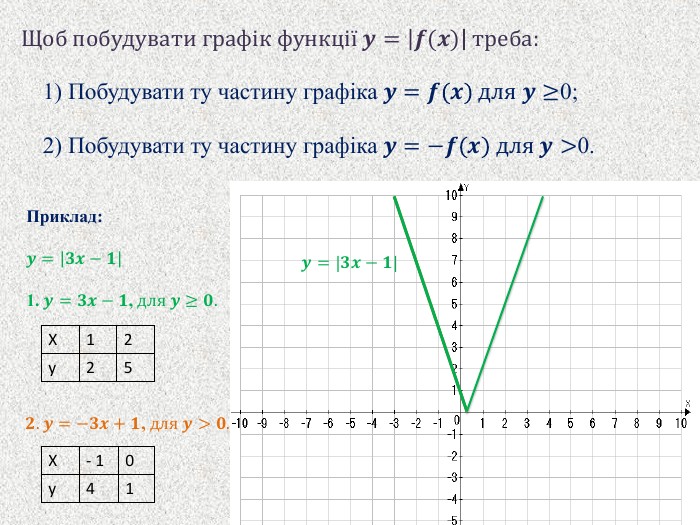
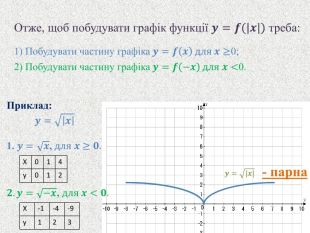
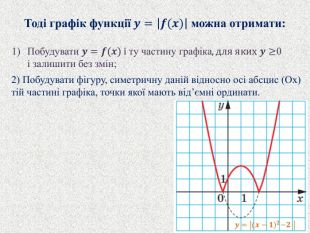
Найпростiшi перетворення графiкiв функцiй. Графіки функцій
Про матеріал
Презентація до уроку з алгебри на тему: "Найпростiшi перетворення графiкiв функцiй. Графіки функцій Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (підручник для класів із поглибленим вивченням математики) 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 2. Квадратична функція Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку