Програма спецкурсу «Математика - наука цікава» 5 клас

КЗ «НВК школа І-ІІ ступенів - ліцей «Гарант»

 

 

 

 

 

Програма спецкурсу

«Математика - наука цікава»

5 клас

 

 

 

 

 

 

 

 

учитель математики

                                                                                          Л. В. Антіпіна

                                                                                                           

Лисичанськ 2018 р.

ПОЯСНЮВАЛЬНА ЗАПИСКА

    Найважливішим завданням школи є підготовка високоосвіченої, всебічно розвиненої людини, озброєної глибокими й міцними знаннями. В учневі необхідно виховувати  прагнення  безперервного вдосконалення знань і вміння самостійно поповнювати їх та застосовувати на практиці.

     З метою розвитку різних інтересів і здібностей учнів у загальноосвітніх школах вводяться спецкурси з математики. Навчання математики в основній школі передбачає, перш за все, формування предметної математичної компетентності, сутність якої подана в розділі «Державні вимоги до загальноосвітньої підготовки учнів» у навчальній програмі для учнів 5-9 класів загальноосвітніх шкіл.

    Основною особливістю сучасного розвитку системи математичної освіти є орієнтація на широку диференціацію навчання математики, що дозволяє вирішити два завдання. З одного боку, забезпечити базову математичну підготовку, а з іншого, сформувати в учнів стійкий інтерес до предмета, виявити і розвинути їх математичні здібності.

   Курс математики 5 класу –  важлива ланка математичної освіти і розвитку школярів. На цьому етапі триває вивчення рахунку, формується поняття змінної і даються перші знання про прийоми рішення лінійних рівнянь, триває навчання розв′язанню текстових задач, удосконалюються і збагачуються вміння геометричних побудов і вимірювань. Геометричний матеріал об'єднано в окремий курс " Геометрична мозаїка". Успішному засвоєнню курсу сприяє вивчення раніше таких понять, як «множина»,  «елемент множини»,  « об'єднання і перетин множин». Велика увага приділяється навчанню дітей  міркувати і наводити прості докази, давати пояснення виконуваних дій. При цьому учнями поступово усвідомлюються правила виконання основних логічних операцій над висловлюваннями. Через шкільну математику лежить шлях до широкого ознайомлення з досягненнями сучасної науки, яка в наш час розвивається особливо швидко.

   Кожна дитина відкрита і сприйнятлива до чудес пізнання, до багатства і краси навколишнього світу. У них є здібності й таланти, треба лише в це вірити і розвивати їх.

Спецкурс з математики в 5 класах є однією з важливих складових програми «Робота з обдарованими дітьми».

Дана програма спецкурсу розроблена відповідно до ідеї реалізації принципів диференційованого навчання учнів.

Мета викладання спецкурсу - залучити учнів до процесу придбання ними математичних знань, умінь і математичної культури.

Основні завдання:

- формування стійких знань з предмета;

- розвиток умінь застосовувати отримані знання на практиці;

- виховання загальної математичної культури;

- розвиток математичного ( логічного ) мислення;

- розширення математичного кругозору;

- підвищення інтересу до предмета і його вивчення;

- вироблення творчого підходу до вивчення математики;

- підготовка до навчання в наступних класах.

  Особлива роль у цій програмі приділяється прищеплюванню навичок самостійності в міркуваннях, у пошуках способів вирішення завдань,

ознайомлення з історичним матеріалом, різноманітними видами задач.

 

 

Структура програми

   Вивчення курсу розраховано на 35годин:  І семестр -16 годин, ІІ семестр - 19 годин.

 Подана програма в табличній формі, яка складається з 3 розділів: розподіл навчального часу; зміст навчального матеріалу і вимоги до навчальних досягнень учнів; зразкове календарно - тематичне планування навчального матеріалу.

     Програма містить такі теми: «Дивовижний світ чисел », «Логічні задачі»,   « Геометрична мозаїка», «Задачі бувають різними: простими і складними »,  «Від гри до знань». Деякі теми спецкурсу пов'язані з програмним матеріалом, а деякі носять самостійний характер.

Особливості організації вивчення спецкурсу

     Заняття можна організувати в таких формах: заслуховування повідомлень учнів або вчителя; колективного обговорення рішень завдань; порівняння методів їх розв′язування; узагальнення пошуку нових шляхів вирішення завдань. Необхідно навчити учнів висувати гіпотези, шукати шляхи доказів, за допомогою проблемних питань створювати дискусії, уміти робити висновки.

      У кінці кожної теми виділено 1 годину для перевірки отриманих знань, якіможна проводити в цікавій формі: захист творчих робіт, змагання, вікторини, ігри, захист презентацій, парад знань і т. ін.

 

 

 

 

5 клас

 Розподіл навчального часу

№ з/п	Тема	Кількість годин
1.	Дивовижний світ чисел	7
2.	Логічні задачі	10
3.	Геометрична мозаїка	5
4.	Задачі бувають різними: простими і складними	10
5.	Від гри до знань	3

 

Зміст навчального матеріалу та вимоги до навчальних досягнень учнів

Кількість годин	Зміст навчального матеріалу	Навчальні досягнення учнів
7.	Тема 1. Дивовижний світ чисел Рахунок у первісних людей. Цифри в різних народів. Знаки арифметичних дій, рівності та нерівності. Обчислювати можна швидше. Пошуки закономірностей.	Учень (учениця): Знає: - як розвивалися цифри в різних народів світу; - історію виникнення арифметичних знаків дій, рівність і нерівність. - прийоми швидкого рахування. Уміє: - швидко рахувати,  вирішувати завдання на знаходження числових закономірностей.
10.	Тема 2.Логічні задачі Множини. Підмножини. Переріз і об'єднання множин. Знаходження загальної частини фігур. Принцип Діріхле. Графи  і розв′язування задач. Кола Ейлера	Учень (учениця): Знає: - основні елементи теорії множин, основні операції над множинами. Уміє:  - виконувати основні операції над множинами; - наводить приклади співвідношень на колах Ейлера. - зображувати відношення між множинами за допомогою кругів Ейлера – Венна. Розв′язує : - задачі з використанням кіл Ейлера, графів та принципу Діріхле,  - задачі на знаходження загальної частини фігур.
5.	Тема 3. Геометрична мозаїка Розповіді про геометрію. Від ліктя до метра. Геометрія на клітчатому папері. Математика в ... сірниковій коробці.	Учень (учениця): Знає: - як зароджувалася геометрія; - як формувалися основні поняття геометрії; - історію розвитку мір і ваги. Розв′язує: - задачі на сірники; - задачі на розрізання фігур на рівні частини. Уміє: - висловлювати одні одиниці вимірів через інші; - малювати фігури на клітчатому папері.
10.	Тема 4.Задачі бувають різними: простими і складними Задачі з українського фольклору. Задачі на переливання. Задачі на зважування. Задачі, які вирішуються з кінця. Задачі без числових даних.	Учень (учениця): Знає: - різні математичні моделі текстових задач. Розв′язує: - задачі на переливання, зважування, задачі без числових даних і задачі, які розв’язуються з кінця.
3.	Тема 5. Від гри до знань Магічні квадрати.  Математичні ребуси. Математична суміш.	Заповнює: - магічні квадрати. Розгадує: - математичні ребуси. розв′язує задачі - жарти.

 

Орієнтовне календарно - тематичне планування курса

№ заняття	Дата	Тема заняття
		Тема 1. Дивовижний світ чисел
1.		Рахунок у первісних людей
2.		Цифри в різних народів
3.		Знаки арифметичних дій, рівності та нерівності
4.		Обчислювати можна швидше
5, 6.		Пошуки закономірностей
7.		Вікторина «Дивовижний світ чисел»
		Тема 2. Логічні задачі
8.		Множини. Підмножини
9,10.		Переріз і об'єднання множин. Знаходження загальної частини фігур
11, 12.		Принцип Діріхле
13, 14.		Графи  і розв′язування задач
15, 16.		Кола Ейлера
17.		Самостійне розв’язування задач
		Тема 3. Геометрична мозаїка
18.		Розповіді про геометрію
19.		Від ліктя до метра
20.		Геометрія на клітчатому папері
21.		Математика в ... сірниковій коробці
22.		Практична робота
		Тема 4.Задачі бувають різними: простими і складними
23.		Задачі з українського фольклору
24, 25.		Задачі на переливання
26, 27.		Задачі на зважування
28, 29.		Задачі, які вирішуються з кінця
30, 31.		Задачі без числових даних
32.		Контрольна робота
		Тема 5. Від гри до знань
33.		Магічні квадрати.
34.		Математичні ребуси.  Математична суміш
35.		Підсумкове заняття

 

 

Зміст

 Пропоновані фрагменти історичних матеріалів складені відповідно до плану спецкурсу.  Наведений матеріал не є вичерпним. Учитель у своїй роботі може включати й інші історичні відомості.

Вступ

 Математику в школі вивчають з 1 по 11 клас. За цей час проводиться багато уроків. Кожен учень повинен добре засвоїти все те, що викладає вчитель. Але для того, щоб надалі можна було опанувати спеціальністю, яка так чи інакше пов'язана з математикою або її застосуванням, цих знань не достатньо. Потрібна самостійна, творча робота і свідоме ставлення до вивчення важкого та дуже необхідного предмета.

Часто учні вважають, що для занять математикою необхідні особливі здібності. Чи так це? Якщо так, то які ж це здібності?

Деякі учні думають, що успіх у вивченні математики заснований на звичайному запам'ятовуванні формул, теорем, правил  і т. ін. Звичайно,гарна пам'ять не завадить, але дуже багато видатних математиків ніякої особливої пам'яттю не володіли. Саме систематичні заняття математикою, уміння знаходити найбільш вдалі методи рішення задач, уміння логічно мислити значно важливіші, ніж пам'ять. Усі ці здібності не даються людині готовими при народженні. Вони розвиваються і міцніють у процесі творчого  вивчення математики. Потрібно тільки любити цю науку й наполегливо займатися нею. Здібності для занять математикою необхідні, але недостатні. Математичний талан - це насамперед важка, добре організована праця над собою.

Часто  говорять,  що математика –  нудна та суха наука, але це так тільки для тих, хто далі вивчення початків математики не пішов. Математика захоплює всіх, хто достатньо вивчив її.

Славнозвісна жінка - математик КОВАЛЕВСЬКА Софія Василівна (1850-1891)писала: «Багато людей, які ніколи не мали нагоди ближче спізнати математику, плутають її з арифметикою і вважають через це наукою сухою та безплідною. Насправді ж це наука, що вимагає якнайбільшої фантазії, і один з перших математиків нашого століття каже абсолютно слушно, що не можна бути математиком, не будучи водночас і поетом у душі». Це висловлювання дуже гарно підходить для епіграфу спецкурсу.

Тема 1. Дивовижний світ чисел

Рахунок у первісних людей

Як же виникла лічба? З давніх-давен люди шукали відповіді на це

запитання. І в різних народів відповідь була неоднакова. Стародавні

греки, наприклад, вважали, що людей навчив лічити Прометей. Той самий,

що за легендою викрав у богів вогонь і віддав його людям. Взагалі

більшість народів появу числа пов'язувала з "діяннями" богів або ж

міфічних героїв. Щоправда, інколи цю заслугу приписували людям, які

насправді жили колись. Автори староруських рукописів, наприклад,

вважали, що лічбу винайшов Піфагор - старогрецький математик, який жив у

VI столітті до нашої ери. Піфагор був великим математиком, але ж люди

вміли лічити задовго до VI століття! І не просто вміли лічити, а й мали

вчених, які писали математичні книги. Найдавніша математична книга

дійшла до нас з другого тисячоліття до нашої ери.

Є підстави вважати, що люди навчилися рахувати 25-30 тисяч років тому. Спочатку люди розрізняли просто один предмет або багато. Минуло дуже багато часу, перш ніж з'явилося число  « два». Рахунок парами дуже зручний, і не випадково в деяких племенах Австралії та Полінезії до  останнього часу були тільки два числівники: один і два. А всі числа, більші двох, отримували назви у вигляді поєднань цих двох числівників, наприклад: три - один, два; чотири - два, два; п'ять - два, два, один і т. ін.

 Найбільш давньою і простою «лічильної машиною» здавна є пальці рук і ніг. І навіть у наш час ще користуються цим давнім рахунковим приладом, який завжди при нас. У давні часи люди ходили босоніж, тому  могли користуватися для рахунку пальцями як рук, так і ніг. Таким чином, вони могли рахувати до 20 .

У селах вживалися рахунки у вигляді зарубок на палицях . Такі насічки на палицях вживалися в торгових угодах. Ці палички після закінчення розрахунків розколювали вздовж на дві половинки, з яких одну брав платник, а іншу - боржник . Одна з половинок виконувала роль квитанції.

  Вже на більш високій стадії розвитку люди за рахунок стали застосовувати різні предмети. Так, одні користувалися для запам'ятовування числа камінчиками, зернами, мотузкою з вузликами, інші - паличками з зарубками (бирками). Це були перші лічильні прилади, які, врешті - решт призвели до утворення різних систем числення і до створення сучасних швидкодіючих електронних лічильних машин.

Цифри в різних народів

    Першими «записами» чисел були зарубки на палиці, на дереві. Однак рисками великі цифри не запишеш, та й читати потім важко й довго. Близько п'яти тисяч років тому в різних народів (у Вавилоні, Єгипті, Китаї) з'явився новий спосіб запису чисел - за допомогою особливих знаків - цифр.

Вавилоняни рахували не десятками, а шістдесятками, тобто 60 одиниць становлять одну одиницю наступного розряду. Наприклад, число 185 вони представляли як 3 рази по 60 і 5. Записувалося таке число за допомогою всього двох знаків, один з яких позначав, скільки разів взято по 60, а інший - скільки взято одиниць. Від цієї шістдесятиричної системи у нас залишився вимір часу. Дійсно, година складається з 60 хвилин, хвилина - з 60 секунд. Поділ кола на градуси, хвилини, секунди теж прийшли до нас від вавилонян.

   У Стародавньому Єгипті, так само як і у нас тепер, рахунок вівся десятками, але запис чисел був дуже громіздким і незручним. Наприклад, для запису двох десятків і двох сотень користувалися різними значками.

 – одиниця, ∩- десять, ୧- сто.

   Сучасні цифри 1,2,3 , ... , 9,0, якими користується більшість народів світу, є найціннішим внеском народів Індії до скарбниці математичних знань. В індусів цифри запозичили араби, від них же ці цифри поширилися в X - XIII ст. в Європі, а потім і в усьому світі. Європейці називали їх арабськими. Ця назва цифр збереглася до наших днів. Те, що одна і та ж цифра може позначати число одиниць, десятків, сотень або тисяч, залежно від того, яке місце (яку позицію) у записі числа вона займає, було великим відкриттям. Воно вражає своєю простотою. Така система нумерації називається позиційною.

На Русі про арабсько-індійську систему знали ще в XIII столітті. Так на одному знайденому дзвоні, виготовленому в ті часи, знаходимо цю нову нумерацію. На початку XVII століття цими цифрами вже нумерують сторінки російських книг, їх карбують на золотих монетах. А в середині століття ними користуються в рукописних працях. У 1703 році в"Арифметиці" Леонтія Магницького усе арифметичне вчення викладене на основі позиційної системи числення, і тільки сторінки підручника позначені слов'янською нумерацією.

До цього наші предки користувалися слов'янською нумерацією. Над літерами ставили титло (риски), тоді ця буква позначала число. Перші десять букв служили для позначення перших десяти чисел, наступні літери позначали десятки , далі – сотні,  наприклад:

                                            

    В основі римської нумерації використаний принцип складання (наприклад, VI = V + I) і принцип віднімання (наприклад, IX = X - I). Римська система нумерації десяткова, але не позиційна. Римські цифри утворилися не від букв, а в первісному вигляді позначалися, як і в багатьох народів, паличками (I - один, X - перекреслена паличка, V - половина від десяти, сто - кружечок з крапкою всередині, п'ятдесят - половина цього знаку і т . д.). Зчасом ці знаки видозмінилися і отримали існуючий тепер вигляд (С - сто, L - п'ятдесят, М - тисяча, D - п'ятсот).

Знаки арифметичних дій , рівності та нерівності

З операціями додавання й віднімання люди мали справузадовго до того, як числа дістали імена. Коли кілька груп збирачів ягід або рибалок складали в одне місце свою здобич, вони виконували операцію додавання. Правда, при цьому додавались не числа, а сукупності (або, як говорять математики, множини) предметів, але операція додавання чисел якраз описує додавання сукупностей предметів. А коли із зібраних горіхів частина використовувалася в їжу, люди виконували віднімання – запас горіхів зменшувався.

       З′явилися знаки дій  у такому вигляді, як ми знаємо, з поширенням у Європі  арабського написання чисел. Звичайно, не всі зразу.

        Першими народилися знаки додавання «+» і віднімання «-». Їх наприкінці ХV століття застосував лейпцігський професор Ян Відман у творі «Швидка і красива лічба для всього купецтва».

        Як же позначали ці дії на письмі? У різних народів по- різному. Єгиптяни, наприклад, коли хотіли додати два числа, схематично малювали дві людські ноги, що «рухалися» вперед, а при відніманні ступні ніг скеровували в зворотному напрямку. В Європі дію додавання ще позначали літерою «р» або «Р» (початкова літера латинського слова «плюс» - більше), а віднімання «m» або «М» (від латинського «мінус» - менше).

         Знак множення «х» - навкісний хрест – знаходимо в праці англійського математика Уїльяма Оутреда «Математичний ключ» (1631- рік). Згодом, у 1698 році, видатний німецький математик Готфрід-Вільгельм Лейбніц дію множення запропонував передавати крапкою (∙), а трохи пізніше, у 1684 році,впровадив дві крапки (:) для позначення ділення. Щоправда, ці знаки дістали загальне визнання і набули поширення лише вXVIII столітті завдяки підручникам німецького математика Хрістіана Вольфа.

    Знак рівності «=» увів англійський учений Роберт Рекорд ще в XVI столітті. На його думку, ніщо не може передати рівність так, як два однакових паралельних відрізки. До нього в математиці користувалися іншими знаками рівності. Так старогрецький математик Діофант відношення рівності позначав літерою «і» ( початкова у слові «ізос» - рівний). Індійські й арабські математики, а також більшість європейських найчастіше, аж до XVII століття вживали для цього  скорочено слово «рівній».

     Знаки «< » і  «>»для позначення відношень нерівності систематично почав застосовувати англійський математик Томас Гарріот. Його книжка, де він вживає ці знаки, побачила світ у 1631 році.

    Дужки круглі знаходимо в математичних творах першої половини XVст. До їхньої появи ставили риски над виразом, якого вони стосувалися, або ж під ним, що було дуже незручно під час друкування.

     Знак ділення й дробу – горизонтальна риска – вперше зустрічається в італійського математика Леонардо Пізанського, який, мабуть, запозичив його з арабських рукописів. Для зручності в друкуванні англієць Август де Морган замінив горизонтальну риску навкісною.

Тема 2. Логічні задачі

Теорія множин

                                                     Під різноманіттям, або множиною,

                                                      я розумію взагалі всяке багато чого,

                                                     яке можна мислити як єдине,

                                                     тобто як сукупність певних елементів,

                                                     яка може бути пов'язана в одне ціле

                                                     за допомогою деякого закону ...

                                                                                                    Георг Кантор

Теорія множин - розділ математики, у якому вивчаються загальні властивості множин - сукупностей елементів довільної природи, які володіють якою-небудь загальною властивістю. Створена в другій половині XIX століття Георгом Кантором за  участю Ріхарда Дедекінда, ця теорія внесла в математику нове розуміння природи нескінченності.

Георг Кантор народився 2 березня 1845 р. в Петербурзі в сім'ї німецького комерсанта , який займався експортом товарів з Росії до Німеччини. Мати Кантора походила з родини відомих віденських музикантів. Відзначають , що музична культура з дитинства зробила вплив на формування особистості майбутнього вченого. Сім'я Кантора була тісно пов'язана з Росією: тут проживали його родичі. Дядько матері, відомий прогресивний юрист Дмитрій Мейер, був професором Казанського університету. Початкову школу Кантор відвідував ще в Петербурзі. Потім родина повертається до    Німеччини, у західне німецьке місто Дармштадт, де хлопчик закінчує реальне училище, отримавши як у школі, так і вдома прекрасну й дуже широку освіту: він володів кількома іноземними мовами, був знавцем стародавніх мов - латини та грецької. Знання мов відкрило йому доступ до праць мислителів минулого - класичної античності і середньовіччя. Ця обставина відіграла важливу роль у становленні теорії множин: Г. Кантор був знайомий з усіма тонкощами в міркуваннях про поняття нескінченності в працях математиків - філософів минулих століть.
       Теорія множин стала основою багатьох розділів математики, загальної топології, загальної алгебри, функціонального аналізу та справила значний вплив на сучасне розуміння предмета математики. У першій половині XX століття теоретико-множинний підхід був привнесений і в  традиційні розділи математики, у зв'язку з чим став широко використовуватися у викладанні математики, у тому числі в школах.
Ключові поняття теорії: множина (сукупність об'єктів довільної природи), відношення належності елементів множини, підмножина, операції над множинами, відображення множин, взаємно-однозначна відповідність.  Поява теорії множин була зустрінута з ентузіазмом багатьма авторитетними математиками. Вони побачили в ній можливість створення метамови математики, тобто формальної одностайної системи понять і принципів, за допомогою якої можна було б викласти з єдиних позицій зміст різноманітних традиційно далеких один від одного розділів математики. Перші такі досить успішні спроби були виконані вже незабаром після виникнення канторівської теорії множин.

Сьогодні теорія множин - це математична теорія, на якій грунтується більшість розділів сучасної математики як неперервної, так і дискретної.

Докладніше з історією виникнення та розвитку теорії множин можна ознайомитись, прочитавши цікаву монографію А.Френкеля і І.Бар-Хіллела "Основи теорії множин" або книгу М.Клайна "Математика. Втрата певності"

 

Принцип Діріхле

Діріхле мав хист поєднувати з мінімумом

 сліпих формул максимум зрячих думок

Г. Мінковський

13 лютого 2014 року минає 209 років з дня народження відомого німецького математика  Петера Діріхле (1805 – 1859 рр.). Визнання він заслужив завдяки ряду відкриттів у алгебрі і теорії чисел, важливих досліджень в області математичного аналізу, вагомих результатів у механіці та математичній фізиці.

Діріхле народився 13 лютого 1805 року в вестфальському місті Дюрені у родині поштмейстера. Його пращури були вихідцями з бельгійського міста Рішле (Richelet), що обумовило незвичне для німецької мови прізвище. Ім'я Лежен має аналогічне походження — діда називали «молодою людиною з Рішле» (фр. le jeune de Richelet).

У 12 років Діріхле почав навчатись у гімназії в Бонні, а через 2 роки — в єзуїтській гімназії в Кьольні, де одним з його викладачів був Георг Ом.

З 1822 по 1827 роки він був домашнім учителем у Парижі, де спілкувався з Фур'є.

1825 року Діріхле разом з Лежандром довів теорему Ферма для випадку n=5. 1827 року він на запрошення Александра фон Гумбольдта обійняв посаду приват-доцента університету Бреслау (Вроцлав). 1829 року він переїздить до Берліна, де працював безперервно 26 років, спочатку як доцент, потім, з 1831 року, як екстраординарний, а з 1839 року як ординарний професор Берлінського університету.

1855 року Діріхле стає спадкоємцем Гауса на посаді професора вищої математики в Геттінгенському університеті. Серед його досягнень — доведення збіжності рядів Фур'є.

При розв’язуванні багатьох задач  користуються способами міркувань, які одержали назву «принцип Діріхле» («принцип висунутих ящиків»). У найпростішій і дотепній формі принцип Діріхле звучить так: »Не можна посадити 7 зайців у 3 клітки так, щоб у кожній клітці було не більше, ніж 2 зайці».

А взагалі твердження формулюється так:

У п клітках неможливо розсадити п + 1 зайців, щоб кожний із них сидів у окремій клітці, тобто знайдеться клітка, де сидить не менше двох зайців.

 

Графи  і розв′язування задач

Теорія графів “відкривалася” незалежно багато разів. Найперша згадка про неї  зустрічається в роботах Ейлера, який у 1736 році розв’язав задачу про

кенігсберзькі мости. У Кенігсберзі було два острови, з’єднаних сімома мостами з берегами річки Прегель та один  з одним (мал. 1). Задача полягала в пошуку маршруту проходження всіх чотирьох частин суші, який

мав починатися на довільній з них, закінчуватися на ній же та по одному разу проходити кожен міст. Проте всі спроби знайти маршрут були невдалими.

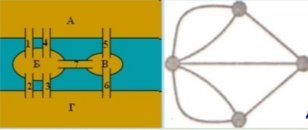Мал. 1. Кенігсберзькі мости та граф

 

Щоб довести неможливість існування такого маршруту, Ейлер позначив кожну частину суші точкою (вершиною, або вузлом), а кожен міст — лінією (ребром), що з’єднує відповідні точки, і одержав “граф” . Твердження про неіснування маршруту тотожне неможливості спеціальним чином обійти граф. Виходячи з цього конкретного випадку, Ейлер узагальнив постановку задачі та знайшов критерій існування обходу.

Пізніше елементи теорії графів з’явилися в таких природничих науках, як

географія, фізика, хімія, електротехніка. Взагалі, графи застосовуються в усіх галузях, де є елементи й зв’язки між ними, тому теорія графів є актуальним прикладним розділом математики.

 

Кола Ейлера

    Скільки гостей Вам зустрічати, якщо збираються друзі з 15 пригощаннями і 20 прикрасами? Чи вистачить усім місця за столом, що вміщує 22 людини ? Перше, що спадає на думку, це 35 осіб. А до чого тут 22 людини ? Є підступ? Звичайно! Адже треба розглянути кілька варіантів.

       Як вирахувати кількість учнів класу, які відвідують одночасно дві або три секції, якщо відома кількість учасників кожної секції окремо? Чи можна навчитися вирішувати такі завдання, плануючи результат?

      Виявляється, такі завдання вирішуються за допомогою кіл Ейлера. Зображення умов завдання у вигляді кіл Ейлера,  як правило, спрощує і полегшує шлях до її вирішення.

      Автор методу - вчений Леонард Ейлер (1707-1783). Він так і говорив про названі його ім'ям схеми: «кола підходять для того, щоб полегшити наші роздуми». Ейлер вважається німецьким, швейцарським і навіть російським математиком, механіком і фізиком. Справа в тому, що він багато років працював у Петербурзькій академії наук і зробив значний внесок у розвиток російської науки.
        До нього подібним принципом для побудови своїх умовиводів керувався німецький філософ і математик Готфрід Лейбніц.
Метод Ейлера отримав заслужене визнання і популярність. І після нього чимало вчених використовували його у своїй роботі, а також видозмінювали на свій лад. Наприклад, чеський математик Бернард Больцано використовував той же метод, але з прямокутними схемами.
Свій внесок зробив також німецький математики Ернест Шредер. Але головна заслуга належать англійцю Джону Венну. Він був фахівцем у логіці й видав книгу «Символічна логіка», у якій детально виклав свій варіант методу (використовував переважно зображення перетину множин).
Завдяки внеску Венна метод навіть називають діаграмами Венна або ще Ейлера-Венна.

Тема 3. Геометрична мозаїка

Розповіді про геометрію

    Про зародження геометрії у Стародавньому Єгипті близько 2000 років до н. е. грецький історик Геродот (V ст. до н. е.) пише так: «Сезостріс, єгипетський фараон, розділив землю, давши кожному єгиптянину ділянку згідно із жеребом та брав відповідний податок з кожної ділянки. Траплялося, що Ніл затоплював ту чи іншу ділянку, тоді потерпілий звертався до царя, а цар посилав землемірів, щоб встановити, наскільки зменшилася ділянка, і відповідним чином зменшити податок.  З’явилася особлива категорія людей, обов’язком яких було розмежувати землі на окремі ділянки. Ця робота виконувалася упродовж багатьох сотень років; у процесі цієї роботи набувались початкові знання про властивості геометричних фігур, вводились нові поняття про ці фігури. Добуті знання передавались наступним поколінням, які додавали до них щось своє, і т.ін. Геометрії в тому розумінні, що ми уявляємо її тепер, у єгиптян не було. Не було символіки, не було аксіоматики, не було доведень. І так виникла геометрія в Єгипті, а звідти перейшла в Грецію». Оскільки  на початку виникнення геометрії в основному йшлося про вимірювання площ земельних ділянок, то стародавні греки, довідавшись про цю науку від єгиптян, назвали її геометрією (від грецьких слів «геос» — земля та «метрео» — вимірюю, отже, слово геометрія означає наука про вимірювання землі).  У стародавній Греції, починаючи з 7 ст. до н.е. з часів Фалеса Мілетського, починається новий етап розвитку геометрії. Вона набуває характерного для неї абстрактного напряму: у ній виникає доведення.

А якби спитати будь-якого з істориків математики, кого з старогрецьких математиків він вважає найвидатнішим, причому дозволяється називати не більше трьох імен, то, мабуть, у більшості випадків відповідь була б така: Евклід, Архімед, Аполлоній. Це справді три кити стародавньої математики, і ніяка, навіть найкоротша, довідка про стародавній світ і його науку неможлива без згадування цих трьох імен.

Евклід  є фокусом, у якому сконцентрувалася уся сучасна математика.

Архімед – геніальний механік і геометр, творець нескінченно малих величин(числення).

Апполоній – творець теорії конічних перерізів.

Минали роки… геометрія збагачувалася новими фактами, змінювала свій вигляд. Були часи, коли вона, як при Платоні або Піфагорі, посідала  гідне місце справжньої цариці наук, а були й періоди, коли вона у своєму розвитку починала відставати від інших, молодих, що бурхливо розвивалися, наук. Але ніколи, очевидно, поки стоїть світ, не настане такий час, коли б людство могло сказати: ось тепер геометрія не потрібна і залишається здати її в архів.

Геометрія була, є і буде постійною супутницею людини на всьому шляху її розвитку, у всій її довгій, складній і цікавій еволюції.

Від ліктя до метра

   У різних народів за різних часів існували свої міри довжини й ваги. У стародавніх арабів, наприклад, найменшою мірою довжини був поперечник макового зерняти. Сім макових зернят складали більшу одиницю вимірювання, що дорівнювала поперечнику гірчичного зерна. Міряли араби і ячмінними зернами, і фалангами великого пальця.

Римляни за одиницю міри площі - югер - брали площу, яку могла зорати за день пара волів. А в Сибіру була міра довжини бука. Це віддаль, на якій людина перестає розрізняти роги бичка.

На початку XII століття англійський король Генріх І видав грамоту про міри довжини. На вулицях Лондона оповісники по кілька разів голосно читали це королівське веління. У ньому говорилося, що віднині зразком міри служитиме рука його величності короля.

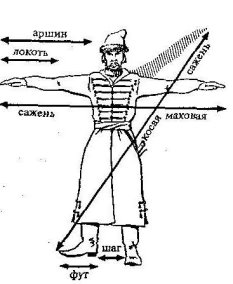Такий наказ нікого не здивував, бо в ті часи населення країни вимірювало товари власними руками й ногами-ліктями й футами.

Лікоть - міра довжини, що дорівнювала віддалі від ліктя до кінця середнього пальця правої руки, - прийшов у Європу зі Сходу разом з арабами в раннє середньовіччя. Фут (в перекладі з англійської - "ступня") - це європейська міра довжини, яка дорівнює довжині людської ступні. Але ж руки і ступні в людей неоднакові. От і наказав король, щоб не було ніякого ошуканства, взяти мірою довжини його, королівську руку - від кінчика пальця до ліктя.

 У 1789 році було розв'язано дуже важливе для міжнародних торгових зв'язків питання. Французькі вчені вирішили, що за одиницю довжини найкраще взяти одну сорокамільйонну частину Паризького меридіана. Цій мірі дали грецьку назву - "метр". Від метра походить дециметр (1/10 його частина), сантиметр (1/100 частина) і міліметр (1/1000 частина).

У дореволюційній Росії була надзвичайно строката система мір. Та, власне, ніякої такої системи й не було. Поряд із старими слов’янськими мірами користувалися деякими англійськими, що прийшли ще за часів Петра І. Тут безборонно співіснували верста, сажень, аршин, вершок, фут, дюйм, географічна і морська милі.

І лише 14 вересня 1918 року Рада Народних Комісарів прийняла постанову про введення в країні метричної системи мір.

Декрет, підписаний Леніним, зобов'язував повністю перейти на нові міри до 1 січня 1922 року.

Тлумачний словничок деяких мір

Аршин - від персидського «арш»(лікоть), старовинна міра довжини. На Русь аршин прийшов 500 років тому разом з купцями з далеких східних країн.

Дюйм - від голландського «дюїм» (великий палець), міра довжини. Дорівнює 2,54 см.

Лінія - дуже маленька одиниця довжини, всього 2,54 міліметра. У Росії лініями вимірювали два види предметів: нижній діаметр скла для гасових ламп і калібр гвинтівки або кулемета.

Метр - від грецького «метрон» (палиця для вимірювання). Це основна одиниця довжини, рівна одній сорокамільйонній частині Паризького меридіана.

Миля - від латинського «міліа» (тисяча). Колись милею називали відстань у тисячу подвійних кроків.

Сажень - від слова "саджати" (малося на увазі саджати молоді деревця). Означає відстань між великими пальцями витягнутих убік рук.

Фут - міра довжини, у перекладі з англійської означає «ступня».

Ярд - англійська одиниця довжини; 1 ярд дорівнює З футам.

Доба - це час, протягом якого Земля обертається навколо своєї осі; 1 доба = 24 год.

Календар - від латинського «календаріум», боргова книжка. За календарем можна полічити великі проміжки часу - місяці, роки, століття, можна одержати відповіді на запитання: «Яке сьогодні число?» і «Скільки минуло років?»

Місяць - одна з мір часу (від двадцяти восьми днів до тридцяти одного).

Рік - це час, за який Земля обертається навколо Сонця; за рік змінюють один одного чотири пори року; 1 рік =12 місяцям = 365 або 366 добам.

Тиждень - це сім днів, які йдуть один за одним. Кожен з днів має свою назву: неділя - коли «не роблять ніякого діла», тобто відпочивають, понеділок - одразу після неділі, вівторок - Другий (вторий) день, (Середа - середина, четвер - четвертий, п'ятниця - п'ятий, субота, по-єврейськи - шабаш, тобто день, коли не працюють.

Хвилина - проміжок часу; з 60 хвилин складається година.

Вузол - одиниця швидкості морських суден; вузол - це морська миля за годину або 1,85 кілометра за годину.

Градус - у перекладі з латинської означає «крок», «ступінь». Градусами вимірюють різні величини - кути і дуги, температуру.

Бал - з французької, означає «м'яч», «куля». Ним оцінюють знання і поведінку, силу землетрусу і густину льоду, майстерність спортсмена і хмарність неба, силу вітру, якість землі тощо.

Математика у … сірниковій коробці

    Відомо, що раніше, до винаходу сірників, одержати вогонь було дуже складним завданням. Люди терли палички, ловили склом сонячні зайчики, вибивали іскру з каменів і чого тільки не придумували для того, щоб одержати вогонь.

     І тільки наприкінці XVIII століття завдяки французькому хімікові Клоду Бертолле з'явилися так звані «сірники - маканки». Це такі палички, на які наносилася бінокль сіль, і запалювалися вони після того, як палички із сіллю вмочали в розчин сірчаної кислоти. Відбулася ця подія в 1805 році.

Але вже в 1927 році англійцеві Джонові Уолкеру спала на думку ідея нанесення на палички такої суміші, що легко запалювалася при терті об наждаковий папір. Таким чином, губилася необхідність носити із собою пухирець із сірчаною кислотою. Ці сірники одержали назву «сухі сірники».

Тоді навіть було налагоджено невелике виробництво таких сірників, але вони мали два істотних недоліки. По - перше, вони дуже сильно смерділи, а по - друге , вони були дуже дорогими. І тому в 1830 році з'явилися нові сірники. Француз Шарль Соріа винайшов сірники, на які наносилася суміш із білого фосфору. Ці сірники не смерділи, але вони були отруйними, і тому в 1855 році хімік - швед дійшов висновку, що можна наносити на сірники червоний фосфор. Результат той же - сірники легко запалюються, але абсолютно безпечні для здоров'я.

     І от, нарешті, у 1889 році відбулася кульмінація розвитку сірників. Була винайдена сірникова коробка. Однак, незважаючи на те, що ії винайшов Джошуа П”юссі, патент на винахід одержала компанія «Diamond Match Company»,компанія, що внесла невеликі зміни в коробку. А саме - винесла смужку «запалювання» на бортик коробки. Раніше вона перебувала всередині.

У Росії перша фабрика, що випускала сірники, була відкрита тільки в 1837 році в Санкт- Петербурзі.

Тема 4. Задачі бувають різними: простими і складними

Задачі з українського фольклора

Одним із аспектів духовної культури народу є фольклор – скарбниця духовних надбань народу.

Народна математика – це сукупність народних математичних знань та навичок, у  основі яких лежать потреби практичної діяльності (необхідність виконання різних арифметичних дій під час проведення землемірних робіт, зведення житла та інших споруд тощо). Недо­ступність професійних математичних знань для широких верств українського населення в минулому зумовлювала вдосконалення найпростіших традиційних прийомів лічби, вимірювання, способів зображення чисел і т. ін.

   В Україні найдавнішими засобами лічби були пальці рук, різні дрібні предмети. Так, рахуючи на пальцях або, як називали, на колодочках, на одній руці налічували 15 «колодочок» із долоні та 15 — з іншої частини цієї ж руки. Із предметів використовували картоплини, квасолинки, патички та ін. Для зруч­ності лічби існували числові групи: пара, трійка, п'ятірка, десяток, копа тощо. Парами лічили худобу, птицю, хатнє добро (чоботи, підошви); трійками — нитки у прядиві (три нитки складали чис­ницю); п'ятірками — снопи; десят­ками — яйця, гарбузи, кавуни; ко­пами — яйця та снопи.
Українська народна математика мала у своєму арсеналі оригінальні способи зображення чисел. Одиниці позначалися паличками, десятки – хрестиками, сотні – кружечками, тисячі — квадрати­ками. Що ж до дробових чисел, то їх передавали переважно в усній формі з відповідними назвами (половина, чверть, осьмушка, шістнадцятка та ін.). Письмово (невеличкими горизонтальними рисками) зображалися  лише най­більш уживані дроби.

Арифметичні дії виконувалися усно. Існували своєрідні народні назви дій – додати, докласти, відкинути, відлічити. Поширеним був спосіб додавання, коли спочатку додавалися сотні, потім десятки, а в кінці — одиниці. Множили шляхом повторного послідовного додавання. Ділення виконували, підбираючи частку послідовним повторним відніманням.
Українські селяни знали й деякі основи геометрії, зокрема вони мали уявлення про просту й лама­ну лінії, про властивості пара­лельних ліній тощо. У будівництві хат та виготовленні бондарських виробів використовували власти­вості діагоналей прямокутника (щоб побудувати стіни під пря­мим кутом), обчислювали відношення довжини кола до діаметра ( за останній приймали третину довжини кола). Бондарі та теслярі вміли користуватись циркулем. Розписуючи хати, побутові виро­би, селяни використовували різні геометричні фігури. Українцям були відомі оригіналь­ні прийоми визначення відстані до недоступного предмета, виміри площі земельних ділянок різно­манітних форм. Знали й основи механіки, які використовували в будівництві хат, вітряків, куль­тових споруд та ін.
Традиційні метричні одиниці, що були в Україні, походять від давньоруських, утворених за антропометричним принципом, тобто за еталон виміру бралися частини людського тіла. Серед найдавніших народних вимірів місткості є такі, наприклад, як ковток, пригорща, жменя. 

Українські селяни користувалися досить поширеними народними способами виміру площі земель­них ділянок. За основу його бра­лася площа прямокутника розмі­рами 30 х 80 або 40 х 60 сажнів. Ко­ристувалися також офіційними одиницями виміру — десятина. Були і більш давні народні міри –  день, опруг, різа, лан, півланок, одріз, клітка та ін. Деякі з них означали кількість витраченого часу на обробіток певної ділянки або кількість зібра­ного урожаю на певній площі.
       Існував оригінальний народний спосіб вимірювання відстані до недоступних предметів: бриль на­сували на очі так, щоб його край перебував в одній площині з очи­ма і предметом, відстань до якого вимірювалась. Потім відшукували інший, доступний предмет, що знаходився в тій самій площині.
Вимірявши відстань до нього, по­рівнювали її з відстанню до не­доступного предмета.

       Важливою складовою частиною духовної спадщини народу є задачі на матеріалі народної творчості або ж фольклорні задачі. Основною метою цих задач є не стільки забавляти, скільки розвивати здібності людей до логічного мислення, рівень кмітливості і винахідливості, здібність до дотепних міркувань.

    Майже всі задачі, пов’язані з творчістю, мають відношення до властивостей і відношень між реальними об’єктами, які моделюються за допомогою математичних понять (числа, фігури, відношення, рівняння, алгоритму та ін.). Розв’язування цих задач дозволяє  певною мірою усвідомлене або неусвідомлене застосування певних математичних знань. У більшості фольклорних задач відсутня абстрактність, характерна для математичних задач. У розв’язаннях цих задач проявляється народна мудрість і винахідливість,  причому без використання будь-яких математичних знань.

     Задачі на матеріалі народної творчості мають велику різноманітність як у відношенні мови і життєвих ситуацій, так і за рівнем складності.

До фольклорних задач належать питання, які базуються на синонімах. Питанням надається форма числової задачі, а тому той, хто знаходить відповідь замість того, щоб відповісти на просте питання, намагається розв’язати її як задачу. Наприклад: « Мужик купив козу за три карбованці. По чому коза дісталась?». По чому? Більшість розуміє: «в скільки обійшлась», «скільки коштує» і замість того, щоб відповісти «по землі», дає відповідь «три карбованці».

Ще в такому плані  питання: «Після семи років, що козі буде?» (Піде 8-мий), «Чи може дощ йти два дні підряд?» (не може, тому що між днями ніч).

До фольклорних задач бажано проявляти інтерес, враховуючи те, що в них закладена народна мудрість, мудрі міркування, кмітливість, вони вчать співставляти, міркувати, здогадуватись, проявляти спритність. Ці задачі мають цікаві мовні і стилістичні особливості, і цим самим привабливі і цікаві. У деяких задачах уміло використано діалог, мовні форми, які характерні народним казкам. Із змісту задач можна дізнатись про побут людей у давні часи.

Ось декілька прикладів таких задач:

1. Рибалка ловив рибу. На питання: « Скільки риб ти впіймав?» - відповів: «Половину восьми, шість без голови, дев’ять без хвоста». Скільки риб впіймав рибалка?   (о) 
2. Летіли горобці і сіли на стовпці, як сіли  по одному – один горобець зайвий, як сіли по два – один стовпець зайвий. Скільки горобців і скільки стовпців? (було три стовпці і чотири горобці).
3. П’ять братів хотіли розділити 20 овець так, щоб кожен отримав непарну кількість. Чи можливо так зробити? (ні, братів непарна кількість).

Міри маси і рідини
З розвитком обміну продуктів виникла потреба в їх вимірюванні за допомогою мір об'єму. Сипкі тіла та рідини міряли, наповнюючи ними посудину певної місткості. Так з'явилися одиниці вимірювання сипких тіл та рідин. Але в цих мірах був великий різнобій. 

     Отже, сипкі тіла та рідини в Україні міряли такими мірками:

1.    Пуд - 16 кг (1 мірка).
2.    Корчак — 2 відра.
3.    Бочка — 40 відер.
4.    Лукно — 4 відра.
5.    Відро — 12,5 л.
6.    Цебер — 3 відра.
7.    Пляшка — 0,77 л.
8.    Кварта —  л.
9.    Крігель (гальба) — 0,5 л.
10.    Синжап - 100 г.
11.    Кубка-0,5 л.
12.    Фелея — 2,5 л.
13.    Деко - 10 кг.
14.    Кіло - 1 кг.
15.    Корець - 100 кг.
16.    Фунт - 0,4 кг.
17.    Око – 1-- л.
18.    Корець — 10 деко.
19.    Колода — 4 корці.
20.    Маца - 62,5 л.
21.    Лашт — ЗО корців.
22.    Гарнець — 4 л.
23.    Чвертка — 25 кг.
24.    Гелетка — 25 кг.
25.    Гарчик — 1,5 кг.
26.    Кавуш — 5 кг.
27.    Мацьок — 50 кг.
28.    Літерка — 1-- ока.

     На Поділлі зерно вимірювали корцями. Бочку називали куфою, ними возили чумаки вино з Криму. Мірами 5—17 користувалися на Буковині. На Дрогобиччині були й свої міри 18—28, якими в основному користувалися для вимірювання зерна. Міру 9 використовували для вимірювання об'єму пива, а міру 11 — для об'єму молока.

Задачі на зважування

Перша документальна згадка про ваги належить до другого тисячоліття до нашої ери.

Це були ваги у вигляді рівноплечого коромисла з підвішеними чашками, і використовувалися вони в Древньому Вавілоні і Єгипті. Пізніше з'явилися нерівноплечі ваги з пересувною гирею. А в IV столітті до нашої ери Аристотель вивів їх теорію – правило моментів сил.

У XII столітті арабський учений аль-Хазіні описав надточні (звичайно для того часу) ваги з чашками, погрішність яких не перевищувала 0,1%! Вони застосовувалися для визначення щільності різних речовин і дозволяли розпізнавати сплави, виявляти фальшиві монети і відрізняти коштовні камені від фальшивих. У 1586 році Галілей сконструював спеціальні гідростатичні ваги для визначення щільності тіл.

З моменту винаходу вагів людей стало хвилювати питання їх точності. Навіть у Біблії сказано: «Невірні ваги – мерзенність перед Господом, але правильна вага –  угодна йому». Можливо, тому перші зразки мір і вагів зберігалися в церквах і монастирях, а першими «повірниками» були церковні служителі.

Бажання не просто чесно торгувати, але  при цьому самому не бути обдуреним, змусило задуматися про найпростіші стандартизації мір і ваги. Тому в Росії в 996 році князь Володимир повелів ввести єдині міри ваги, а в Указі князя Всеволода (XII століття) вперше була згадана щорічна перевірка вагів. У 1723 році Петро I видає Указ про те, щоб борошно, крупу, солод і толокно продавати на вагу, а не на міру, і в «заорленні ваги», тобто повірені і тавровані, «а якщо в кого з'явиться фальшива міра і ваги, оний буде жорстоко оштрафований ».

У 1841 році з ініціативи міністра фінансів Росії на території Петропавлівської фортеці побудували «особливу негорючу будівлю» – Депо зразкових мір і ваги. Туди торговці зобов'язані були приносити на перевірку свої вимірювальні прилади. Далі за ініціативою Менделєєва в Росії була організована Головна палата мір і ваги. А Декрет 1918 говорить «Про введення міжнародної метричної десяткової системи мір і ваги: Прийняти за основу одиниці ваги – кілограм».

До кінця ХХ століття видозмінювалися й удосконалювалися механічні ваги. Зараз же їм на зміну прийшли електронні, які в самий найближчий час остаточно витіснять механічні.

Тлумачний словничок деяких мір

Золотник - російська одиниця маси. Нею вимірювалася маса золотих виробів.

Кілограм - головна одиниця маси; народився він наприкінці XVIII ст. у Франції.

Пуд - стародавня міра маси, дорівнює 16 кг.

Фунт - міра маси. Походить від латинського слова "пондус" (вага, гиря), становить 450 г.

Тема 5. Від гри до знань

Магічні квадрати

    Назву магічних (чарівних, таємничих) квадрати одержали від арабів, які вбачали в  таких числових властивостях і сполуках дещо неземне та  містичне і вважали  такі квадрати талісманами. Історія виникнення магічних квадратів сягає  сивої давнини. Найбільш ранні
відомості про такі  квадрати містять  китайські книги, написані у  IV-V ст. до н. е.

Найвідомішим із стародавніх  магічних квадратів є  Ло-шу (2200 р. до н. е): таблиця з дев'яти клітинок, заповнена числами  від 1 до 9.І сьогодні його можна побачити на амулетах, які носять у Східній Азії та Індії.

 

 

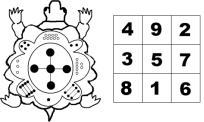
 Наступні за часом відомості  про магічні квадрати дійшли до нас із   Індії та Візантії. 
Способами складання магічних квадратів займалися
відомі  математики А. Різе, М. Штіфель( ХVI ст.), 

А. Кірхер, Баше де Мезеріак  (XVII ст.) та інші.

 

 

 

У Європі зображення  магічного квадрата вперше з'явилося в гравюрі «Меланхолія» відомого німецького  художника Альбрехта Дюрера. З давніх часів і дотепер дослідження магічних  квадратів процвітало як своєрідний   культ і досить часто було овіяно  містичним    туманом.

 

ОСОБЛИВОСТІ ДЕЯКИХ МАГІЧНИХ КВАДРАТІВ

 

 Найдавніший квадрат четвертого порядку було знайдено в Кхаджурахо (Індія). Цей магічний квадрат належить до так званих «диявольських» (або «пандіагональних») квадратів, ще більш дивовижних, ніж симетричні. Крім звичайних властивостей, такі квадрати є магічними за всіма «ламаними діагоналями». Наприклад, числа 2, 12, 15і  5,а також 2, 15 і  4 стоять на ламаних діагоналях. «Диявольський» квадрат збереже свої властивості, якщо його верхній рядок переставити вниз, або навпаки,   нижній     рядок поміс­тити вгору, а також якщо викреслити  останній стовпець   зліва або  справа і приписати його до квадрата з протилежної  сторони.

        Відомий американський архітектор Клод Ф. Брегдон помітив, що, сполучивши одну за одною клітинки магічних квадратів ламаною, ми  в 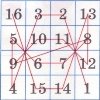більшості випадків дістанемо витончений візерунок. Приклад магічної ламаної показано на малюнку, де візерунок зображено на квадраті Дюрера.

 

Математичні ребуси

   Ребус - загадка, у якій слова або фрази, що розгадуються, зображено у вигляді комбінації зображень, фігур, композицій з букв і таке інше. Саме слово «ребус» походить від латинської фрази «Nonverbissedrebus», що означає «Не словами, а за допомогою речей». Загалом, термін «rebus» асоціюють з латинським словом rebis: res (річ, предмет), rebis (перетворення). 
    Кожен з нас неодмінно зустрічався з ребусами в повсякденному житті. Безперечно, найвідоміший та розповсюджений ребус виглядає так: i ♥ u (вимовлятися  англійською мовою «I Love You» - «Я тебе люблю»). У сучасному розумінні, ребус -  це, передусім, загадка, що складається із зображень предметів (малюнків у поєднанні з буквеними композиціями та іншими знаками), співзвучних зі словами або частинами слів розгадки. Кілька ребусів можуть бути об'єднані в одному малюнку або у вигляді послідовності малюнків з тим, щоб скласти фразу або речення. У літературних ребусах для складання речень використовуються букви, числа, музичні ноти або особливим чином розташовані слова. Ребуси можуть передавати пряме значення слів, головним чином, щоб інформувати або інструктувати неграмотних людей, або навмисне приховувати їх значення, щоб інформувати тільки обраних. Однак найчастіше ребуси використовують як загадки і розваги. 
Використання примітивних зображень, як засобу передачі інформації, стало підґрунтям для формування ранніх писемних систем давньоєгипетської культури (рубіж 4-го і 3-го тисячоліть до нашої ери). Рання форма ребуса зустрічається в малюнковій писемності, де абстрактні слова, складні для зображення, були представлені зображеннями предметів, назви яких промовляються аналогічним чином. Пізніше зображення ребусів використовувалися для передачі назв міст на грецьких і римських монетах. Ребуси залишалися популярними в Середні віки - їх зображували на будівлях або об'єктах володіння, для позначення роду. 
Використовувати ребуси в якості загадок або жартів розпочали в XV столітті у Франції. Спочатку ребусом називали особливого роду балаганні виступи, що містять пасквілі, якими паяци в Пікардії щорічно потішали народ під час карнавалу. В алегоричній формі комедіанти висміювали  вади та слабкості сильних світу цього. Своїм виступам автори дали латинську назву "De rebus quae geruntur", тобто «На злобу дня» (дослівно «про справи, які діються»). 
У ХVI ст., коли забави ці були заборонені адміністрацією, характер ребуса змінився. Ребусом почали називати каламбур, побудований на грі слів. Найчастіше це була загадка, що складається із зображень різних предметів (часто упереміж з буквами, цифрами та музичними нотами), назви яких не позначають понять, але подібні з ними за вимовою або співзвуччям (не звертаючи увагу на правопис). 
Перші відомі рукописні збірники ребусів датовані кінцем XV початком XVI століття. У 1582 (? 1562) році з'явився перший друкований збірник під назвою "Les Bigarurres du Seigneur des Accords", що мав великий успіх і витримав кілька видань. Автором його був Етьєнн Табуро (Etienne Tabourot, 1548-90) - французький поет, відомий під ім'ям seigneur des Accords, чудовий "віршомаз", що запам'ятався скоріше віршованими фокусами (акровіршами, анаграмами і т.ін.), аніж дійсно поетичними творами. 
Його книжка являє собою цілий трактат про ребуси. Однак малюнків у ній всього з десяток. Більшість ребусів Табуро передає у формі жартівливих оповідань. Так, наприклад, якийсь абат на наказ залишити абатство відповів: "Я витратив 30 років на вивчення перших двох літер абетки (А.В.) і бажаю мати стільки ж часу на ознайомлення з двома наступними літерами" (С.D.). Під А.В. він мав на увазі абатство (abbaye), a під С.D. - дієслово "ce der" (поступитися). З літературної сфери ребус поширився у Франції на дворянські герби, вивіски торгових закладів та навіть з'явився на могильних пам'ятниках і в молитовниках. З Франції мода на ребуси перейшла в Італію, Англію та Німеччину. 
Кількасот ребусів майстрів XVII - XIX століть зберігаються, зокрема, в Лондонському музеї. Приміром, 1639 роком датується робота флорентійського гравера і художника Стефано делла Белла (Stefano della Bella), виконана у формі овального картуша під назвою "Ребус на вдачу". 
У 1783 році англійський художник і гравер Томас Б’юїк (ThomasBewick) в лондонській друкарні Т.Ходжсона (T.Hodgson) друкує незвичайну Біблію для дітей, у якій події Святого Письма переказуються у формі ребусів. Виконана таким чином Біблія стала іменуватися "ієрогліфічною". У ній деякі слова з тексту замінені картинками з метою переказати історію в прямий, простий і цікавий спосіб. Через кілька років, у 1788 році, американський видавець Ісайя Томас (IsaiahThomas) видає ієрогліфічну Біблію за океаном. Такі незвичайні ієрогліфічні Біблії стали дуже популярними наприкінці XVIII століття, оскільки полегшували викладання Святого Письма дітям. 
Англійський письменник і математик Чарльз Лютвідж Доджсон, більш відомий під псевдонімом Льюїс Керролл, один із найпопулярніших  дитячих письменників XIX століття, автор казок «Аліса в Країні чудес» і «Аліса в Задзеркаллі», часто використовував ребуси в численному листуванні з юними шанувальниками своєї творчості . У своїх листах, а їх було близько 100 тисяч (!), він часто заміняв частини слів малюнками або зображав букви у дзеркальному відображенні. Для розшифрування таких загадкових листів потрібна була неабияка кмітливість, а це дуже подобається дітям. 
У другій половині XIX століття ребуси стали широко застосовуватися в повсякденному житті. Їх зображували на сторінках газет і журналів, поштових листівках, столовому приладді. У законодавиці мод - Франції, випустили цілу серію фаянсових тарілок, на одному боці яких був зображений ребус, а на звороті - розгадка.
У Росії перші ребуси з'явилися на сторінках журналу "Илюстрация" у 1845 році. Пізніше, у 1881 році починає видаватися спеціалізований "Еженедельный загадочный журнал «Ребус», у якому, крім захоплюючих головоломок, публікувалися цікаві статті про виховання дітей, психологію, різні новини з усього світу, белетристика. За правильні відгадки загадок, ребусів і шарад читачі отримували невелику грошову премію та призи. 
Бурхливий розвиток обчислювальної техніки, інформаційних технологій і телекомунікацій також опинилося під впливом ребусів. На рубежі століть, із зростанням популярності мобільного зв'язку сформувався особливий SMS-сленг, основною характеристикою якого стала стислість. Буквально це означало, чим менша кількість букв або знаків - тим краще. Саме тому «мова SMS» набула усіляких абревіатур і скорочень. Зі зростанням популярності Інтернету і соціальних мереж цей напрямок усіляко перетворювався і доповнювався новими словами. Ось лише декілька прикладів сучасного комп'ютерного сленгу: «cul8r» (see you later), «b4» (before), «gr8» (great). Подібно ребусу окремі букви і цифри замінюються співзвучними словами і виразами. Окремо варто також згадати про "смайл" - простий та ефективний засіб вираження емоцій, без якого спілкування у мережі просто неможливо уявити.

          Повідомлення історичних відомостей з математики є однією із форм виховання на уроках спецкурсу. Систематичне введення матеріалу з історії математики сприяє кращому засвоєнню науки, викликає інтерес до неї,    робить її не такою «сухою», якою вона здається багатьом учням.

       Учні повинні твердо знати, що математика є продуктом творчої діяльності людського генія протягом тисяч років, а не хитра вигадка «мудреця». Кожна теорема - це узагальнення величезного досвіду людства. Математика виникла і розвивалася для задоволення безперервно зростаючих потреб людського суспільства.
     На конкретних прикладах слід показувати учням, як розвивалися математичні поняття і відношення, теорії і методи, знайомити їх з іменами та біографіями видатних учених, які створювали математику.
Форми повторення можуть бути  різноманітними. В одному випадку вчителю слід самому нагадати про ту чи іншу подію, у іншому - поставити перед учнем або перед усім класом питання; може статися, що учень за своєю ініціативою запропонує історичний матеріал.

Як показує досвід роботи в школі, є багато можливостей використання історико-математичного матеріалу на заняттях спецкурсу. Елементи математичної логіки, прийоми обчислювальної математики, основи програмування, точніше кажучи, усі розділи математики  можна і корисно вивчати з залученням історико-математичного матеріалу.

 

Література

1. Аменицкий Н. Н., Сахаров И. П. Забавная арифметика. – М.: Наука, 1991.

2. Богданович М. Математичне джерельце. – К.: Веселка, 1988.

3. Кордемский Б. А. Удивительный мир чисел. – М.: Просвещение, 1986.

4. Кравчук В., Янченко Г. Математика. 5 клас. – 3-тє вид. – Тернопіль: Підручники й посібники, 2002. – 272 с.

5. Нагибин Ф. Ф. Математическая шкатулка. – М.: Просвещение, 1964.

6. Олехнин С. Н., Нестеренко Ю. В., Потапов М. К. Старинные занимательные задачи. – М.: Наука, 1988.

7. Перельман Я. И. Занимательная математика. – М.: Наука, 1976.

8. Скляренко О. В. Математика. Задачі для розвитку мислення. 6 клас. – Харків: Торсінг плюс, 2006.

9. Скобелев Т. М., Берман В. П. Математика в позаурочний час. – К.: Радянська школа, 1973.

10.  Шеврин Л.Н., Гейн А. Г., Коряков И. О. Учебник –     собеседник для 5-6 классов. – М.: Просвещение, 1989.

11. Ясінський В. А. Цифри і системи числення // Математика в школах України. – 2003. - № 28 (40).

12. Калужнин Л.А. Элементы теории множеств и математической логики в школьном курсе математики.Пособие для учителей.М., «Прсвещение», 1978. 88 с. с. ил.

13. http://ito.vspu.net/SAIT/inst_kaf/kafedru/matem_

14. Ганчев И, Математический фольклор/ И. Ганчев, К. Чиняев, И. Стоянов. - М.: Изд-во «Знание», 1987.

15. Капица О.И. Детский фольклор/ О.И Капица. – Л: Прибой, 1928 г..

16. Довженок Г.В Дитячий фольклор/ Г.В. Довженок. - К.: Наук думка, 1984 р.

17. Державна національна програма "Освіта" ("Україна XXI століття")

18. http://rebus1.com/ua/index.php?item=history