Методичні рекомендації "МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ З МЕХАНІКИ"
Комунальний заклад «Ліцей «Максимум»
Кропивницької міської ради»

МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ З МЕХАНІКИ
Бузько Вікторія Леонідівна учитель фізики,
спеціаліст вищої кваліфікаційної категорії, учитель-методист, кандидат педагогічних наук
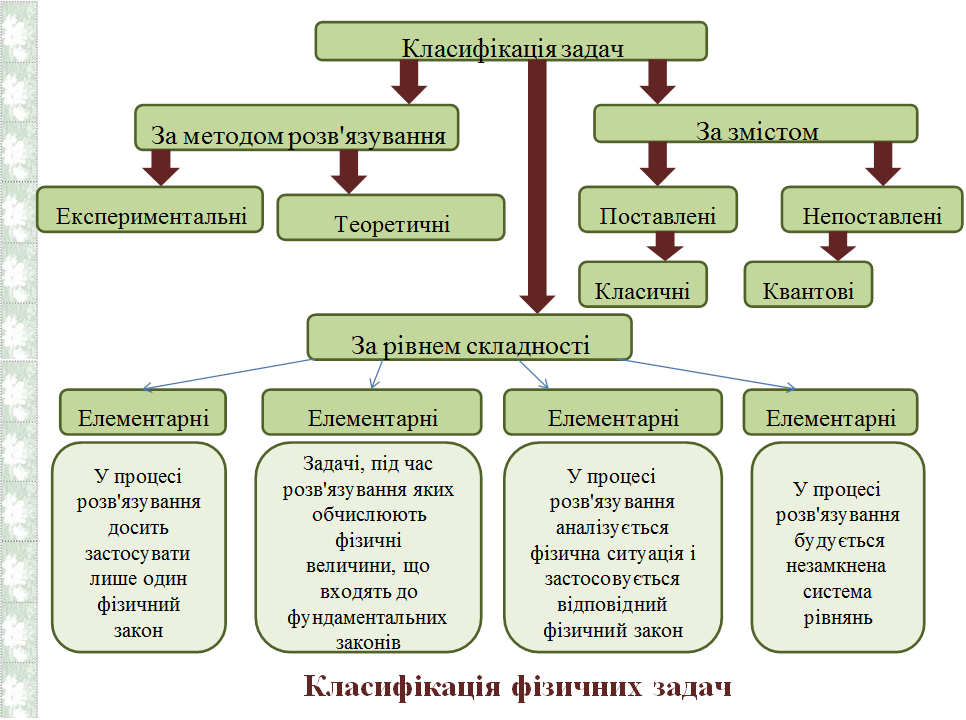
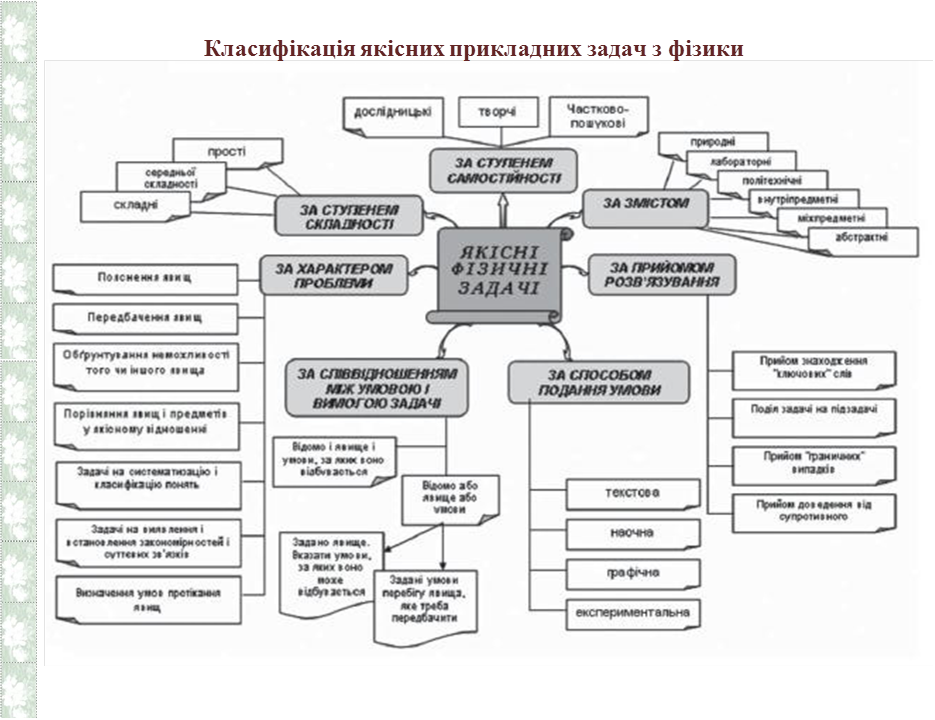
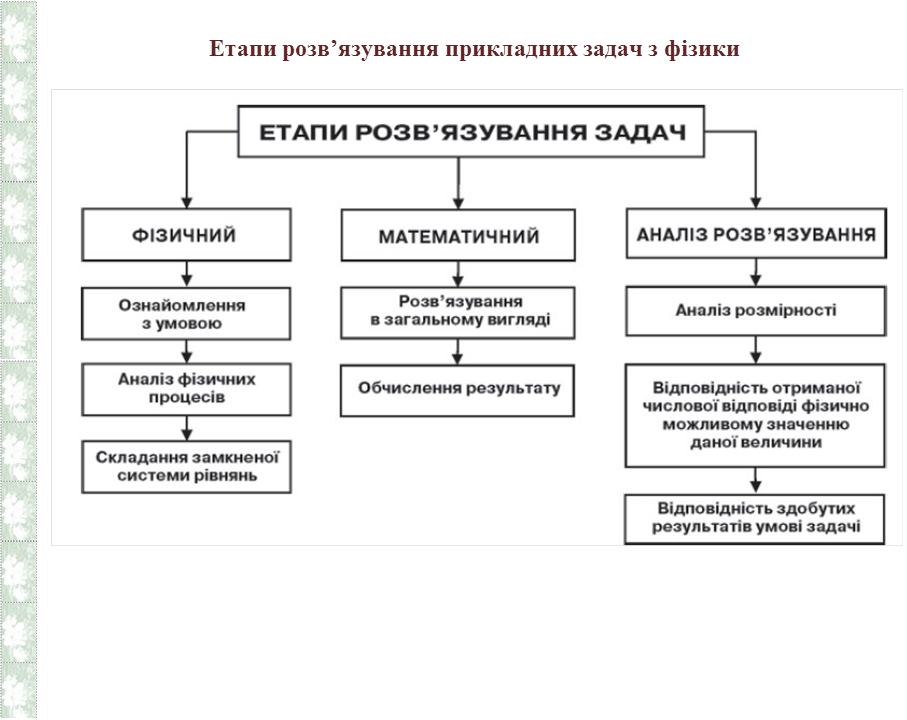
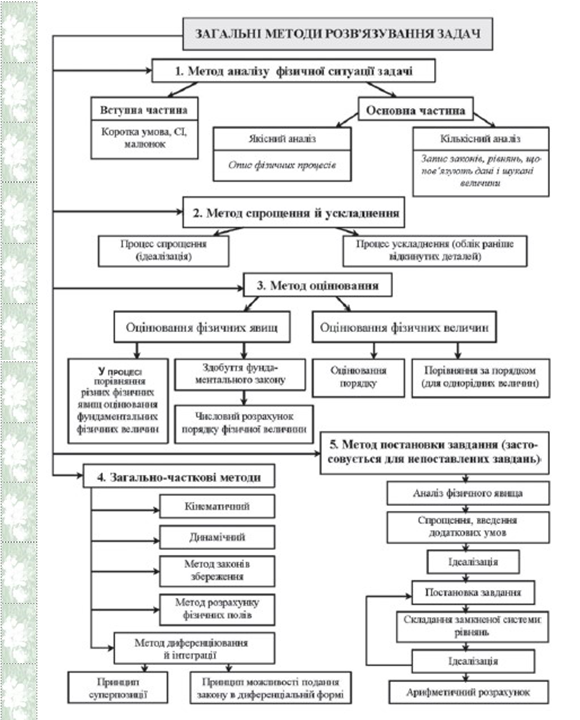 ©Бузько В. Л., 2022
©Бузько В. Л., 2022
• Дослідницькі – це задачі, предметом вивчення яких є фізичні явища, процеси, факти і відповідні моделі.
• Класифікація навчальних дослідницьких задач:
• дослідження побудованих моделей;
• ![]() дослідження відмінностей між ідеальними моделями та їх реальними прообразами
дослідження відмінностей між ідеальними моделями та їх реальними прообразами
(об’єктами, явищами, процесами);
• розроблення моделі експерименту; формулювання висновків спостережень та експериментів;висунення, формулювання та перевірка гіпотез;
• добір засобів вимірювання тощо.
Схема 3. Блок-схема «Загальний метод розв'язання задач» В.І.
Одінцової і Н.Є. Кургаєвої
|
Етап I. Побудова моделі ситуації, наведеної в завданні |
Крок 1. Виділити в тексті завдання структурні елементи фізичного явища:

![]() 1) матеріальний об'єкт, про зміну стану якого йде мова; 2) інший матеріальний об'єкт, з яким перший взаємодіє (що впливає об'єкт);
1) матеріальний об'єкт, про зміну стану якого йде мова; 2) інший матеріальний об'єкт, з яким перший взаємодіє (що впливає об'єкт);
3) вплив і умови, при яких воно здійснюється; 4) результат впливу (або взаємодії).
Крок 2. Перевести їх на фізичний мову.
Крок 3. Уявити модель схематично і записати умову задачі.
|
Етап II. Складання рівнянь, що описують модель ситуації |
|
|
Етап III. Висновок формули для знаходження шуканої фізичної величини |
|
|
Етап IV. Перевірка отриманої формули |
|
|
Етап V. Обчислення значення шуканої фізичної величини і контроль відповіді |
|
Правила розв’язування задач з кінематики

![]() 1.Зробити схематичний малюнок, на якому показати траєкторію руху точки і вибрану систему відліку.
1.Зробити схематичний малюнок, на якому показати траєкторію руху точки і вибрану систему відліку.
2. Визначити вид руху вздовж кожної з координатних осей.
3.Для кожної осі показати на малюнку всі кінематичні характеристики руху:
початкову швидкість, прискорення, кінцеву швидкість, переміщення.
4.Записати кінематичний закон руху у векторній формі і в проекціях на вибрані осі координат.
5.Розв’язати отриману систему рівнянь і знайти шукану величину.



Правила розв’язування задач на закон додавання швидкостей
1.Зробити схематичний малюнок, на якому показати задані тіла і швидкості їх руху.
2.З’ясувати, рух якого тіла буде розглядатися в дані й задачі.
3.Вибрати тіла, відносно яких буде розглядатися рух даного тіла, і зв’язати з ними нерухому і рухому системи відліку.
4.Швидкостям, що показані на малюнку, присвоїти буквені індекси.
5.З’ясувати, в якій системі відліку раціональніше розв’язувати задачу.
6.У вибраній системі відліку записати у векторній і скалярній формі необхідні кінематичні рівняння, з яких можна знайти шукану величину.
 7.Записати закон додавання швидкостей у векторній формі і в проекціях на вибрані осі координат. Якщо вектори швидкостей направлені під кутом один до одного, то дозволяється геометричне розв’язання одержаного трикутника швидкостей.
7.Записати закон додавання швидкостей у векторній формі і в проекціях на вибрані осі координат. Якщо вектори швидкостей направлені під кутом один до одного, то дозволяється геометричне розв’язання одержаного трикутника швидкостей.
8.Розв’язати всі одержані рівняння і знайти шукану величину.




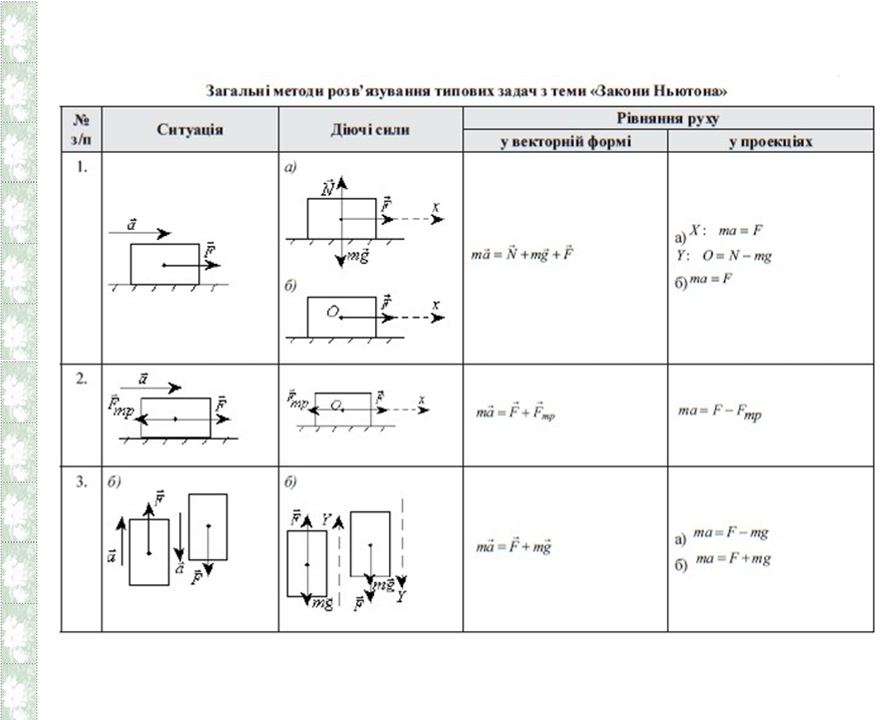
Алгоритм розв’язування задач з динаміки
1. Уважно прочитайте умову задачі. З’ясуйте, які сили діють на тіло та характер руху тіла (рухається тіло рівномірно чи з прискоренням; якою є траєкторія руху тіла).
2. Запишіть коротко умову задачі, виразіть числові значення СІ.
3. Зробіть схематичний рисунок, покажіть на ньому обрану систему відліку та всі сили, що діють на тіло.
4. Запишіть другий закон Ньютона у векторному вигляді та проекціях на осі координат.
5.  Запишіть додаткові рівняння (наприклад, формули для сил або рівняння кінематики з урахуванням початкових умов: початкових координат та швидкостей тіла).
Запишіть додаткові рівняння (наприклад, формули для сил або рівняння кінематики з урахуванням початкових умов: початкових координат та швидкостей тіла).
6. Розв’яжіть отриману систему рівнянь у загальному вигляді.
7. Проаналізуйте отриманий результат (перевірте одиниці величин).
8. Виконайте числові розрахунки, оцініть правдоподібність результатів.
9. Запишіть відповідь.
10. Обміркуйте, чи має задача інший спосіб розв’язування?
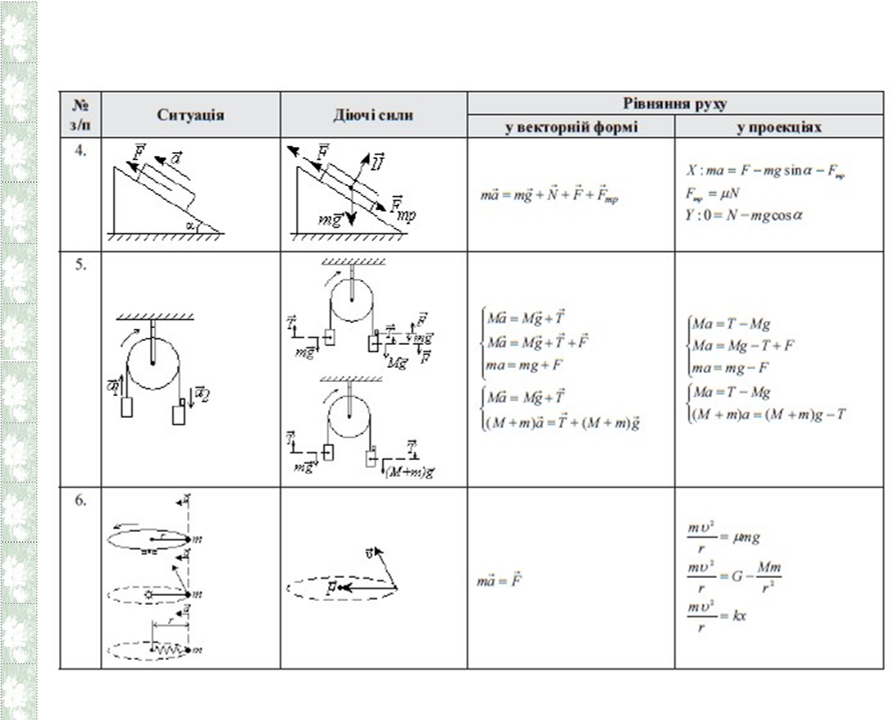
![]()
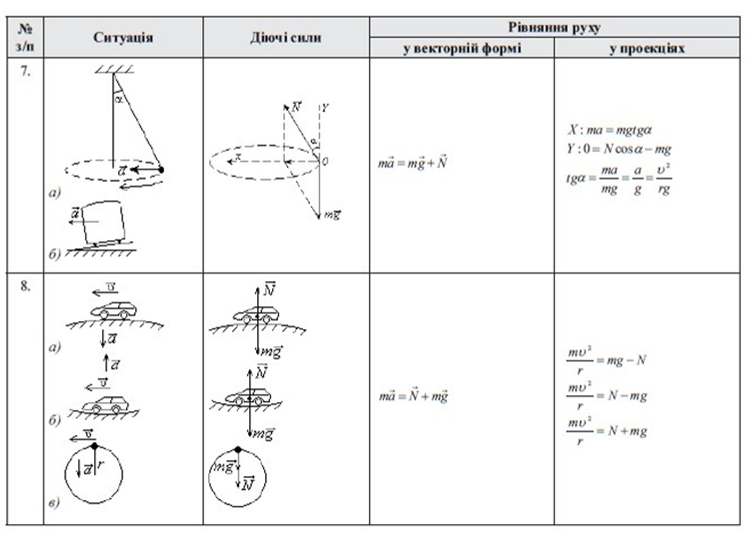
![]()
 |
Часткові способи розв’язування прикладних фізичних задач
|
Способи розв’язування прикладних фізичних задач |
|
Механіка |
|
|
|
|
Розділи |
|
||
|
Кінематика |
Статика |
Динаміка |
Закони збереження |
|
|
Координатний |
+ |
+ |
+ |
|
|
Векторний |
+ |
+ |
+ |
|
|
Графічний |
+ |
+ |
+ |
+ |
|
Симетрії |
+ |
|
|
+ |
|
Визначення центра мас |
|
+ |
+ |
+ |
|
Віртуальних переміщень |
+ |
+ |
+ |
+ |
|
Енергетичний |
+ |
+ |
+ |
+ |
|
Подібності |
|
+ |
|
+ |
|
Розмірностей |
+ |
+ |
+ |
+ |
|
Аналогій |
|
+ |
|
+ |
20 
15

 |
10
5
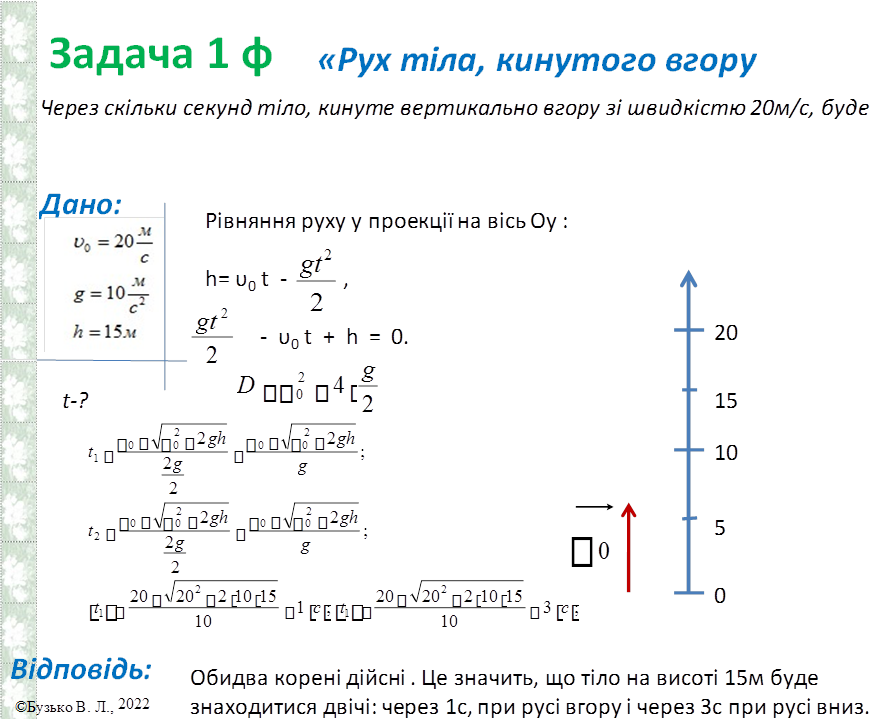 0
0  на висоті 15 м від початкового положення? Розв'язування:
на висоті 15 м від початкового положення? Розв'язування:

h 02 2gh

Задача 2
«Рух тіла по похилій площині»
![]() • По похилій площині пустили котитися знизу вгору кульку. На відстані L=30см двічі: через t1=1с і через t2=2c після початку руху. Вважаючи рух рівноприскореним, визначте початкову швидкість і прискорення руху кульки.
• По похилій площині пустили котитися знизу вгору кульку. На відстані L=30см двічі: через t1=1с і через t2=2c після початку руху. Вважаючи рух рівноприскореним, визначте початкову швидкість і прискорення руху кульки.
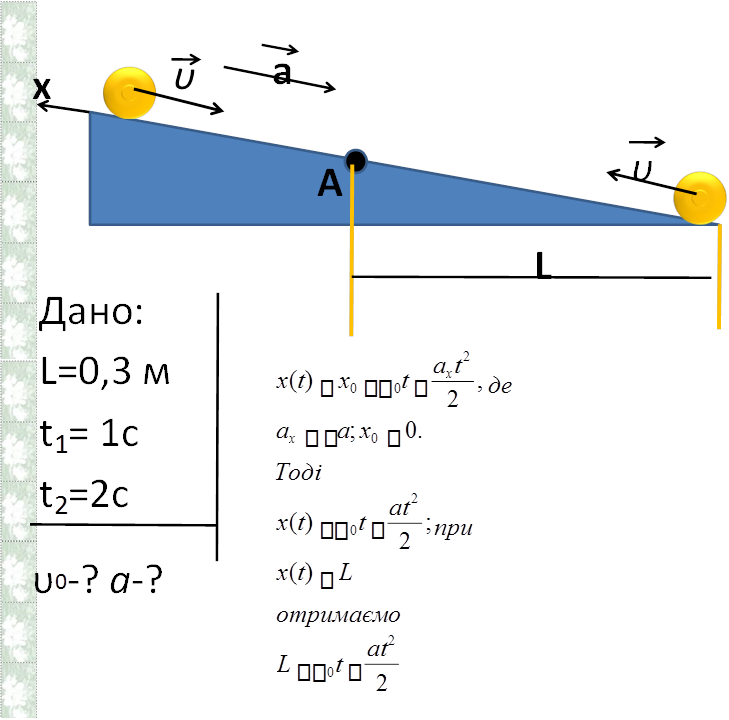
Перепишемо рівняння у стандартному виді
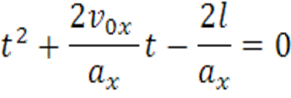
![]() За теоремою Вієта:
За теоремою Вієта:
20x
t1 t2 ![]()
ax
![]() 2L t1t2
2L t1t2 ![]() ax
ax
2L a ![]()
t1t2
 a
a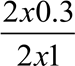 0.3м/с2
0.3м/с2 
0x ![]() (t1 t2)ax 2
(t1 t2)ax 2
0x 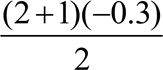 0.45м/с2
0.45м/с2
Перепишемо рівняння в стандартному виді
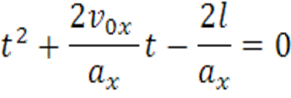
 За теоремою Вієта (математика):
За теоремою Вієта (математика):
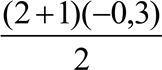
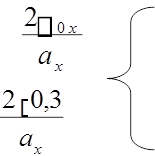
![]() 1[1] 3
1[1] 3![]() 2ax0x a 20,3 0,3 м/с2
2ax0x a 20,3 0,3 м/с2
2
12 2 ![]() 2a0x,3 0x (t1 t2)ax
2a0x,3 0x (t1 t2)ax
 Рух тіла під дією кількох сил по горизонтальній площині.
Рух тіла під дією кількох сил по горизонтальній площині.
![]() При швидкості 20м/с водій вимикає двигун і починає гальмування по горизонтальній ділянці дороги з коефіцієнтом тертя 0,2. Визначити час, через який
При швидкості 20м/с водій вимикає двигун і починає гальмування по горизонтальній ділянці дороги з коефіцієнтом тертя 0,2. Визначити час, через який
зупиниться
автомобіль, його прискорення та гальмівний шлях.
Алгоритм розв’язання задач на закон збереження імпульсу
1. Прочитайте умову задачі.
2. З'ясуйте основне питання задачі і які тіла взаємодіють.
3. Стисло запишіть умову задачі.
4. З'ясуйте, в яких напрямах система замкнута
5. Зробіть креслення, вказавши вектори імпульсів.
6. Запишіть закон збереження імпульсу для заданих тіл у векторній формі.
7. Виберіть систему відліку.
8.  Переведіть векторну форму запису закону збереження імпульсу для даного випадку в скалярну (в проекціях на вибрані осі координат).
Переведіть векторну форму запису закону збереження імпульсу для даного випадку в скалярну (в проекціях на вибрані осі координат).
9. Вирішіть рівняння щодо шуканих величин
10. Перевірте правильність знайденого розв’язання шляхом операцій з найменуваннями величин.
11. Підставте в розв’язання загального вигляду числові значення величин в СІ і проведіть обчислення.
12. Оцініть достовірність отриманого результату.
©Бузько В. Л., 2022
Задача 3
«Задача на закон збереження енергії»
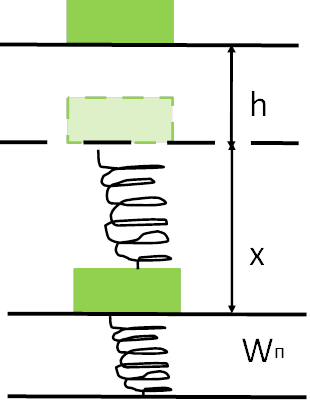
![]() • Вантаж масою m=5кг падає з висоти h=0,5м на легку підставку, прикріплену до пружини жорсткістю k=700
• Вантаж масою m=5кг падає з висоти h=0,5м на легку підставку, прикріплену до пружини жорсткістю k=700 ![]() Нм . Визначте максимальне зміщення пружини х (коливань немає).
Нм . Визначте максимальне зміщення пружини х (коливань немає).
«Задача на закон збереження енергії»
Розв'язування:
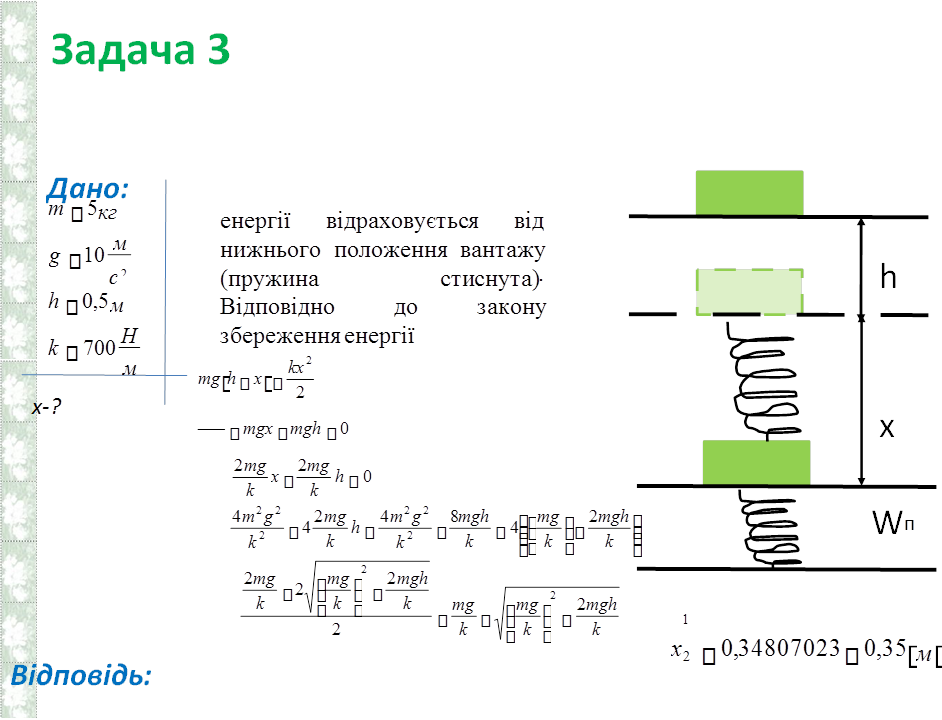 Нульовий рівень потенціальної
Нульовий рівень потенціальної
kx2 2 x2
D
x1,2 x 0,2052131 0
Х1<0, Х2=0,35м.
«Задача на закон збереження енергії»
Розв'язування:
Нульовий рівень потенціальної енергії відраховується від нижнього положення вантажу
(пружина стиснута). Відповідно до закону збереження енергії
kx2
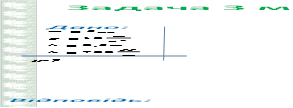 mghx
mghx![]()
2
kx2
![]() mgxmgh 0
mgxmgh 0
2
700x2
![]() 50x25 0
50x25 0
2
350x2 50x25 0 / :25
14x2 2x1 0
7x2 x0,5 0
x1 0,2052131 0 x2 0,34807023 0,35м
Х1<0, Х2=0,35м.
Бінарні уроки і експериментальні задачі.
Проведення бінарних уроків у процесі навчання фізики дозволяє вирішити проблему роз'єднаності навчальних предметів, що дає можливість:
![]()
![]() розширювати інформаційну поглиблювати і насиченість уроку. деталізувати вивчення;
розширювати інформаційну поглиблювати і насиченість уроку. деталізувати вивчення;
встановлювати зв'язки між
різними поняттями і
підвищувати мотивацію їх практичну спрямованість;
навчально-пізнавальної діяльності учнів і їх творчий потенціал
за рахунок нестандартної форми уроку;
![]() Експериментальні задачі, це задачі, розв’язування яких органічно пов'язані з експериментом: з вимірюванням, відтворенням фізичних явищ, спостереженнями за фізичними процесами, роботою з обладнанням.
Експериментальні задачі, це задачі, розв’язування яких органічно пов'язані з експериментом: з вимірюванням, відтворенням фізичних явищ, спостереженнями за фізичними процесами, роботою з обладнанням.
![]() Розв’язуючи експериментальні завдання, учні переконуються на конкретних прикладах, що отримані ними знання під час уроків фізики дозволяють вирішувати практичні завдання.
Розв’язуючи експериментальні завдання, учні переконуються на конкретних прикладах, що отримані ними знання під час уроків фізики дозволяють вирішувати практичні завдання.
![]()
![]() Види експериментальних задач у формуванні фізичних
Види експериментальних задач у формуванні фізичних
|
Види задач |
Роль експериментальнихпонять задач у формуванні фізичних понять |
|
Випереджаючі |
|
|
Попередні: |
дозволяють здійснити введення ознак нового поняття, представляючи їх як елементи вже вивченого поняття, попереднє знайомство з ознаками нового поняття, створення проблемної ситуації на уроці. |
|
Перспективні: |
дозволяють поступово підготувати учнів до засвоєння важкодоступного в даний момент поняття, вивчення якого передбачається при вивченні наступних тем курсу. |
|
Супутні: |
здійснюється формування понять: дається їх визначення, відбувається розширення обсягу та встановлення зв'язків між ними; сприяють відпрацюванню і закріпленню вивченого поняття, його існуючих ознак. |
|
Завершальні: |
дозволяють узагальнити і систематизувати отримані знання учнів, сприяють формуванню поняття на рівні теоретичного і філософського і узагальнення. |
©Бузько В. Л., 2022
Визначити масу лінійки.
Обладнання: вимірювальна лінійка, важок відомої маси (1…5 г), круглий олівець.
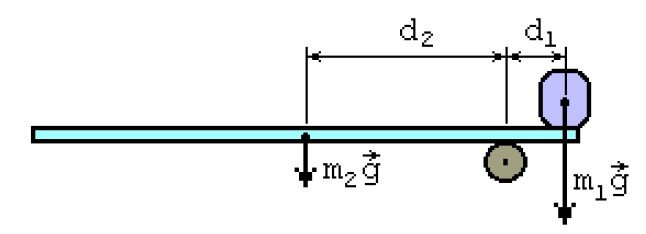
![]() Розв’язання. Встановимо на кінці горизонтально розміщеної лінійки важок масою m1 (рис.). Потім переміщуючи під лінійкою круглий стержень, підберемо таке положення осі обертання, при якому вся система перебуватиме в рівновазі. При цьому момент сили тяжіння m1g, яка діє на важок, дорівнюватиме моменту сили тяжіння m2g, яка прикладена до центру мас лінійки: m1gd1 = m2gd2. Звідси: m2= m1d1/d2.
Розв’язання. Встановимо на кінці горизонтально розміщеної лінійки важок масою m1 (рис.). Потім переміщуючи під лінійкою круглий стержень, підберемо таке положення осі обертання, при якому вся система перебуватиме в рівновазі. При цьому момент сили тяжіння m1g, яка діє на важок, дорівнюватиме моменту сили тяжіння m2g, яка прикладена до центру мас лінійки: m1gd1 = m2gd2. Звідси: m2= m1d1/d2.
Відлічивши прямо по шкалі лінійки величини плечей d1 та d , обчислимо її масу.
Визначити положення центру мас довгої неоднорідної палиці.
Обладнання: неоднорідна палиця довжиною 0,5…0,8 м (можна використати указку).
Розв’язання: 1. Шляхом спроб можна знайти на палиці місце, поклавши яким на палець чи ребро долоні, вдасться привести її до стану рівноваги. Центр мас палиці буде знаходитись над ребром долоні.
Розв’язання 2. Можна покласти палицю горизонтально на ребра долонь обох рук і потім почати повільно їх наближати. Ребра долонь завжди зійдуться під центром мас палиці (рис.).
![]() Пояснити це можна так. Коли ребро однієї долоні наближається до центру мас палиці, то сила тиску на ребро зростає. Це приводить до збільшення сили тертя і рух даної руки відносно палиці припиняється. Сила ж тиску палиці на ребро іншої руки при цьому зменшується, що приводить до зменшення сила тертя палиці по ребру цієї долоні. Внаслідок цього, вона рухається до центру мас палиці. Через декілька таких «кроків» ребра долонь зійдуться під центром її мас. Це є цікавим прикладом саморегульованості процесу.
Пояснити це можна так. Коли ребро однієї долоні наближається до центру мас палиці, то сила тиску на ребро зростає. Це приводить до збільшення сили тертя і рух даної руки відносно палиці припиняється. Сила ж тиску палиці на ребро іншої руки при цьому зменшується, що приводить до зменшення сила тертя палиці по ребру цієї долоні. Внаслідок цього, вона рухається до центру мас палиці. Через декілька таких «кроків» ребра долонь зійдуться під центром її мас. Це є цікавим прикладом саморегульованості процесу.
Визначити масу лінійки.
Обладнання: вимірювальна лінійка, важок відомої маси (1…5 г), круглий олівець.
![]() Розв’язання. Встановимо на кінці горизонтально розміщеної лінійки важок масою m1 (рис.). Потім переміщуючи під лінійкою круглий стержень, підберемо таке положення осі обертання, при якому вся система перебуватиме в рівновазі. При цьому момент сили тяжіння m1g, яка діє на важок, дорівнюватиме моменту сили тяжіння m2g, яка прикладена до центру мас лінійки: m1gd1 = m2gd2. Звідси: m2= m1d1/d2.
Розв’язання. Встановимо на кінці горизонтально розміщеної лінійки важок масою m1 (рис.). Потім переміщуючи під лінійкою круглий стержень, підберемо таке положення осі обертання, при якому вся система перебуватиме в рівновазі. При цьому момент сили тяжіння m1g, яка діє на важок, дорівнюватиме моменту сили тяжіння m2g, яка прикладена до центру мас лінійки: m1gd1 = m2gd2. Звідси: m2= m1d1/d2.
Відлічивши прямо по шкалі лінійки величини плечей d1 та d , обчислимо її масу.

Експериментальні завдання: біофізика людини
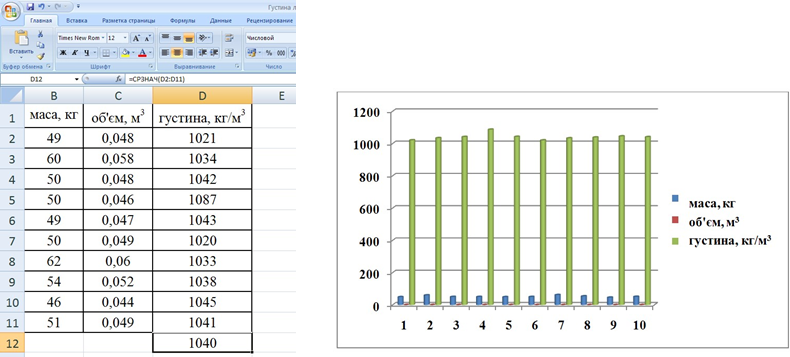
Визначення густини тіла людини
q ![]() Техніка безпеки: дослід необхідно проводити з дозволу батьків і в присутності одного із батьків.
Техніка безпеки: дослід необхідно проводити з дозволу батьків і в присутності одного із батьків.
q Мета: визначити густину свого тіла.
q Обладнання: ванна з водою; маркер, клейка паперова стрічка; скотч, (відро, банки ємністю 3, 2, 1, 0,5 л. ); терези.
Парореактивне сегнерове колесо
![]() Серед переліку стандартного обладнання демонстраційного експерименту з фізики є модель гідравлічної реактивної турбіни, що називається сегнеровим колесом (на честь угорського фізика і математика Яноша Андроша Сегнера, який винайшов цю турбіну). Модель складається з конусоподібної посудини, яка може обертатися навколо вертикальної осі. До нижньої частини посудини прикріплені дві горизонтально розташовані трубки, кінці яких відігнуті у протилежні боки. За допомогою даної моделі можна продемонструвати силу реакції струменя води, що витікає із сопла.
Серед переліку стандартного обладнання демонстраційного експерименту з фізики є модель гідравлічної реактивної турбіни, що називається сегнеровим колесом (на честь угорського фізика і математика Яноша Андроша Сегнера, який винайшов цю турбіну). Модель складається з конусоподібної посудини, яка може обертатися навколо вертикальної осі. До нижньої частини посудини прикріплені дві горизонтально розташовані трубки, кінці яких відігнуті у протилежні боки. За допомогою даної моделі можна продемонструвати силу реакції струменя води, що витікає із сопла.

Визначення середньої потужності, яка розвивається під час бігу на дистанції 60 м
Подолайте дистанцію S=60м, виміряйте час t(с) за який ви подолали дистанцію.________________________________________________________
![]() Вважаючи рух рівноприскореним, обчисліть середню потужність Nср, яка розвивається під час бігу:
Вважаючи рух рівноприскореним, обчисліть середню потужність Nср, яка розвивається під час бігу:
![]() Nср Wt m2t2k 2mst3 2
Nср Wt m2t2k 2mst3 2
за умови s υсрt υk t 2
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
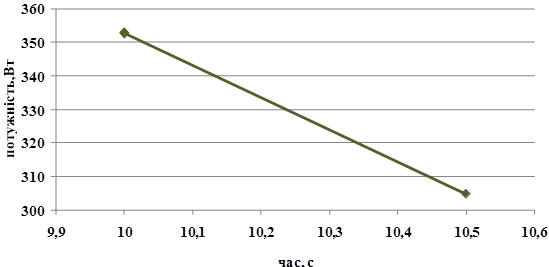
 Визначення середньої потужності, яка розвивається під час бігу на дистанцію 60 м (ученицею 9-го класса)
Визначення середньої потужності, яка розвивається під час бігу на дистанцію 60 м (ученицею 9-го класса)
|
шлях, м |
час, с |
маса, кг |
потужність, Вт |
|
60 |
10 |
|
352,8 |
|
60 |
10,5 |
49 |
304,8 |
|
60 |
10 |
49 |
352,8 |
Потужність, яка розвивається під час бігу
Визначення середньої потужності, яку людина розвиває при присіданні
1. Виміряйте висоту своєї поясниці H
(м).________________________________
2. Виміряйте висоту свого тіла h (м) в положенні «присівши» (центр тяжіння тіла при цьому знаходиться приблизно на висоті
0,5h._____________________
3. Зробіть n присідань за проміжок часу t (с).____________________ 4. Обчислите потужність N, яку ви розвиваєте (Вт). mg
![]() N n
N n ![]() H 0,5h
H 0,5h
t
__________________________________________________________________
__________________________________________________________________
5. Порівняєте результати отриманих вами значень потужності з результатами отриманими іншими учасниками досліду.
__________________________________________________________________
6. Запишіть всі результати, зробіть висновок, запишіть відповідь.
__________________________________________________________________
__________________________________________________________________
Визначення механічної роботи і потужності, яка розвивається людиною при різних видах навантаження
Хід роботи.
1. ![]() Віджатися максимальну кількість разів (хлопчики від землі, дівчинки від лавки). Число віджимань – n;
Віджатися максимальну кількість разів (хлопчики від землі, дівчинки від лавки). Число віджимань – n;
2. За допомогою рулетки визначити висоту підйому щодо лавки або землі – h;
3. Розрахувати роботу за один підйом тіла за формулою А = mgh;
4. Розрахувати загальну роботу n підйомів тіла Aзаг = nA
|
вік |
стать |
m, кг |
n |
h, М |
А, Дж |
|
11 |
жін. |
29 |
6 |
0,4 |
487,2 |
|
12 |
чол. |
37 |
12 |
0,45 |
999 |
Визначити потужність, яка розвивається людиною, при піднятті по сходах (бігом і кроком).
Хід роботи.
1. ![]() За допомогою рулетки виміряти висоту однієї сходинки: S0.
За допомогою рулетки виміряти висоту однієї сходинки: S0.
2. Обчислити число сходинок: n.
3. Визначити висоту сходів: S = S0 . n;.
4. Визначити масу свого тіла: m, кг.
5. Обчислити силу тяжіння, яка діє на ваше тіло: F = mg.
6. Визначити роботу: А = F . S.
|
спосіб |
вік |
стать |
m, кг |
F, Н |
s, м |
А, Дж |
t, с |
N, Вт |
|
Шагом |
11 |
жін. |
29 |
290 |
2,72 |
788,8 |
10,6 |
74,4 |
|
12 |
чол. |
54 |
540 |
2,72 |
1468,8 |
8,4 |
174,8 |
|
|
Бегом |
12 |
чол. |
37 |
370 |
1,65 |
610,5 |
2,9 |
210,5 |
|
11 |
жін. |
29 |
290 |
2,72 |
788,8 |
5 |
1450 |
Визначення крохмалю в картоплі в залежності від його густини в домашніх умовах
Мета: визначити вміст крохмалю в картоплі в залежності від його густини, і визначити для яких цілей його використовувати.
Обладнання: нитки, посудина з водою, сіль, плічки, лінійка, картопля, тіло відомої маси (телефон). Хід роботи:
1. Підготувати картоплю.
2. З плічок виготовила важіль. Взяли телефон Huawei Y6 Pro (TIT-U02), масу якого дізналася за паспор даними (160 г = 0,160 кг). До одного плеча важеля підвісили телефон і виміряли за допомогою лінійк довжину l1. Картоплю перемотали нитками і підвісили до іншого плеча важеля і зрівноважили важіль. Ви плече l2. Дані занесли до таблиці.
|
маса m1, кг маса телефона |
плече важіля l1, м |
F1, Н |
плече важіля l2, м |
F2, Н |
|
0,160 |
0,06 |
1,6 |
0,035 |
2,74 |
![]() З формули моменту сил для важеля М1 = М2, F1l1 = F2l2 знайшли F2 = (F1l1) / l2 За формулою F1 = m1g вирахували силу тяжіння, що діє на телефон.
З формули моменту сил для важеля М1 = М2, F1l1 = F2l2 знайшли F2 = (F1l1) / l2 За формулою F1 = m1g вирахували силу тяжіння, що діє на телефон.
За формулою m2 = F2/g вирахували масу картоплі, g = 10 Н/кг. m2 = 2,74 Н/10 Н/кг = 0,274 кг - маса картоплі.
3. Визначення об’єму картоплі. Об’єм шукаємо з методу плавання тіл.
Картопля в прісній воді тоне, а в солоній воді можна домогтися, щоб він плавав. З умови плавання тіл Fтя можна обчислити об'єм тіла. Fтяж = mg, де m маса картоплі, яку визначили в пункті 2. FА = ρgVт формул
Архімеда. Vт = Fтяж / ρg, де ρ густина солоної води. Vт = 2,74 Н / 1030кг / м3 · 10 Н / кг = 0,000266 м3
4. За формулою ρ = m / v обчислюємо густину картоплі. ρ = 0,274кг / 0,000266 м3 = 1030,1 кг / м3
5. Робимо висновок про зміст крохмалю в картоплі і визначаємо для яких цілей його можна використовуват Картопля, що містить крохмаль <20% від маси бульби, йде на корм худобі. Картопля з вмістом крохм 60% краще використовувати для технічних цілей, наприклад, для переробки на крохмаль і патоку.
Висновок: для нашого картоплі вміст крохмалю <13%, що свідчить про те, що її не можна використовува їжі.
Визначити густину та об’ємну вагу ґрунту.
Обладнання: важільні терези, циліндр-бур, електроплитка, дерев’яний молоток, металевий лист, посудина з водою, масштабна лінійка.
Теоретичні відомості. Вивчаючи основні складові ґрунту, розглянемо три його агрегатні стани: твердий, рідкий та газоподібний. Кожному з них відповідає відповідно густина твердої фази, скелета ґрунту, а також ґрунту у звичайному стані.
![]() Для обчислення густини твердої фази потрібно визначити масу сухого ґрунту в одиниці об’єму. Щоб визначити густину скелета ґрунту, необхідно масу сухого ґрунту в непорушному стані (з отворами і порами) розділити на його об’єм. З метою виконання експериментальної роботи потрібно виготовити циліндр-бур для взяття проб ґрунту й утримання його в непорушному стані. Для цього можна використати металеву трубу діаметром 8–9 см довжиною 10–12 см. Один кінець труби загострюють. Об’єм циліндра обчислюють за формулою: V = πR2h, де R – радіус внутрішньої частини циліндра-бура; h – його висота. У практиці часто виникає потреба здійснювати обчислення об’ємної ваги різних речовин, у тому числі й ґрунту:
Для обчислення густини твердої фази потрібно визначити масу сухого ґрунту в одиниці об’єму. Щоб визначити густину скелета ґрунту, необхідно масу сухого ґрунту в непорушному стані (з отворами і порами) розділити на його об’єм. З метою виконання експериментальної роботи потрібно виготовити циліндр-бур для взяття проб ґрунту й утримання його в непорушному стані. Для цього можна використати металеву трубу діаметром 8–9 см довжиною 10–12 см. Один кінець труби загострюють. Об’єм циліндра обчислюють за формулою: V = πR2h, де R – радіус внутрішньої частини циліндра-бура; h – його висота. У практиці часто виникає потреба здійснювати обчислення об’ємної ваги різних речовин, у тому числі й ґрунту:
d = ρg, де d – об’ємна вага; ρ – густина; g = 9,81 Н/кг.
©Бузько В. Л., 2022
Визначити густину та об’ємну вагу ґрунту.
Алгоритм розв’язування експериментальної задачі такий:
1. Дерев’яним молотком забити циліндр-бур у ґрунт.
2. Обкопати ґрунт навколо забитого циліндра до його основи.
3. Підрізати його лопаткою на рівні нижньої основи циліндра.
4. Не відриваючи лопатки, накрити листком жерсті або картону і перевернути.
5. ![]() Визначити масу ґрунту в звичайному стані.
Визначити масу ґрунту в звичайному стані.
6. Обчислити його густину: ![]()
7. Обчислити об’ємну вагу в звичайному стані: d = ρg.
8. Висипати ґрунт на лист металу і просушити, не допускаючи згорання органічних речовин.
9. Визначити масу сухого ґрунту.
10. ![]() Обчислити густину скелета:
Обчислити густину скелета:
11. Обчислити його об’ємну вагу
Література
Галатюк Ю.М., Рибалко А. В. Впровадження системи дослідницьких задач в курсі фізики середньої школи [Текст] / Ю.М Галатюк, А. В. Рибалко // Сучасні технології в науці та освіті: збірник наукових праць. В 3-ох томах.– Кривий Ріг: Видавничий відділ КДПУ, 2003.– Т 2.– С. 49–55.
Гончаренко С. У. Фізика: методи розв’язування задач [Текст] / С. У. Гончаренко // 2-е вид.– К.: Либідь, 1996.– 128 с.
Готуємось до олімпіад з фізики. – Х.: Вид.група “Основа”, 2005. – 208с. – (Б-ка журн. “Фізика в школах України”. Вип.9 (21)).
![]() Жук Ю. О. Розв’язування дослідницьких задач з фізики із застосуванням нових інформаційних технологій [Текст] / Ю. О. Жук // Наук.-метод. зб.: Проблеми освіти.– Вип. 6.– Київ, 1996,– С.57–63.
Жук Ю. О. Розв’язування дослідницьких задач з фізики із застосуванням нових інформаційних технологій [Текст] / Ю. О. Жук // Наук.-метод. зб.: Проблеми освіти.– Вип. 6.– Київ, 1996,– С.57–63.
Мельник Ю. С. Задачі прикладного змісту з фізики у старшій школі / Ю.С. Мельник // Навчально-методичний посібник. – К.: Педагогічна думка, 2013. – 120 с.
©Бузько В. Л., 2022
![]()
©Бузько В. Л., 2022


про публікацію авторської розробки
Додати розробку

