Департамент освіти, науки та молодіжної політики

Івано-Франківський обласний інститут післядипломної педагогічної освіти

 

 

 

Власна методична розробка

на тему:

 

РЕАЛІЗАЦІЯ

МЕТОДУ МАТЕМАТИЧНОГО  МОДЕЛЮВАННЯ

ПРИ РОЗВ’ЯЗУВАННІ СЮЖЕТНИХ ЗАДАЧ

В ПОЧАТКОВИХ КЛАСАХ

 

 

 

вчителя початкових класів

Калуської загальноосвітньої школи І-ІІІ ступенів №3

Серман Оксани Богданівни

 

 

 

 

 

 

 

                                      Івано-Франківськ

2017 р.

ЗМІСТ

 

1. Огляд і аналіз літератури

2. Опис власного досвіду

3. Результативність впроваджуваного досвіду

     4.Методичні рекомендації щодо застосування методу
математичного моделювання при розв’язуванні сюжетних задач в початкових класах

5. Список використаної літератури

6. Додатки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Огляд і аналіз літератури

 

 

У ході вивчення психолого-педагогічної, філософської, методичної літератури були розглянуті різні визначення поняття «модель» і «моделювання» та їх класифікації.

З усіх визначень цих понять можна виділити основні риси моделі:
модель заміщає об’єкт – оригінал, зберігає деякі важливі властивості об’єкта – оригіналу,  результати дослідження моделі переносяться на оригінал.

Питання моделювання розглядалися в роботах філософів (В.А.Штоффа, І.Б. Новікова, Н.А. Уйомова та інших), фахівців з педагогіки і психології  (Л.М. Фрідмана, В.В. Давидова). Поняття «модель» виникло в процесі дослідного вивчення світу, а саме слово «модель» походить від латинських слів «modus», «modulus», що означають міру, образ, спосіб. Н.А.Уйомов визначає модель як «спрощену картину реального світу, яка становить собою безліч взаємопов’язаних припущень про світ, і є простіше тих явищ, які вона за задумом відображає або пояснює». Розглянемо класифікацію запропоновану  Л. М. Фрідманом. З точки зору ступеня наочності він всі моделі розбиває на два класи: матеріальні (речові, реальні) та  ідеальні.

До матеріальних моделей відносять такі, які побудовані з будь-яких речових предметів: металу, дерева, скла та інших матеріалів. До них також відносять і живі істоти, які використовуються для вивчення деяких явищ або процесів. Всі ці моделі можуть бути безпосередньо чуттєво пізнані, бо вони існують реально, об’єктивно. Вони є речовим продуктом людської діяльності.

Ідеальні моделі ділять зазвичай на три види:

• образні (іконічні);
•  знакові (знаково-символічні);
•  уявні (розумові).

До образних відносять різного роду малюнки, креслення, схеми, що передають в образній формі структуру або інші особливості модельованих предметів чи явищ.

Знаково-символічні моделі становлять собою запис структури або деяких особливостей об’єктів, що моделюються за допомогою знаків-символів якоїсь штучної мови. Прикладами таких моделей є математичні формули, рівняння.

Нарешті, уявні моделі – уявлення про будь-яке явище, процес або предмет, що виражають теоретичну схему модельованого об’єкта.

Математичне моделювання – є найважливішим видом знакового моделювання і здійснюється засобами мови математики, його елементи завжди розглядаються разом з певними перетвореннями, операціями над ними.

Математичне моделювання передбачає використання в якості специфічного засобу дослідження оригіналу його математичну модель, вивчення якої дає нову інформацію про об’єкт пізнання, його закономірності.

Математичною моделлю називають опис якого-небудь реального процесу на мові математичних понять, формул і відносин. Математична модель – це спрощений варіант дійсності, використаний для вивчення її ключових властивостей. З математичними моделями тісно пов'язаний математичний метод пізнання об’єктів – метод математичного моделювання. Співвідношення між елементами a, b і c, яке виражається формулою a + b =c, – це математична модель. Вона ізоморфно відображає операцію об’єднання двох «куп яблук» з їх числовим значенням a і b в загальну «купу яблук», яких виявиться  c = a + b. У цьому сенсі операція додавання ізоморфна цього злиття. Цей приклад пояснює загальний математичний метод пізнання.

Метод математичного моделювання полягає в тому, що для дослідження якого-небудь об’єкта вибирають або будують інший об’єкт, в якомусь відношенні подібний досліджуваному. Побудований або вибраний об’єкт вивчають і з його допомогою вирішують досліджувані завдання, а потім результати вирішення цих завдань переносять на первинне явище або об’єкт.

Математичне моделювання – наближений опис якого-небудь класу явищ зовнішнього світу, виражене за допомогою математичної символіки. Це потужний метод пізнання зовнішнього світу, а також прогнозування. Математичне моделювання розширює творчі можливості учня у вирішенні цілого ряду завдань. Сучасний школяр повинен «добре знати» математику, тобто не просто вміти виконувати різні розрахунково-обчислювальні операції, а й розуміти математичні методи дослідження та їх можливості. Тільки розуміння сутності математичного моделювання дозволяє адекватно використовувати цей метод у розв’язуванні сюжетних задач.

На сьогоднішній день найбільш поширеною є трьохетапна схема процесу математичного моделювання:

1) переклад запропонованого завдання з природної мови на мову математичних термінів, тобто побудова математичної моделі задачі (формалізація);

2) розв’язання задачі в рамках математичної теорії (розв’язання всередині моделі);

3) переклад отриманого результату (математичного розв’язання) на мову, якою була сформульована вихідна задача (інтерпретація отриманого розв’язку).

Найбільш відповідальним і складним є перший етап – сама побудова математичної моделі. Він здійснюється логічним шляхом на основі глибокого аналізу досліджуваного явища (процесу) і вимагає вміння описати явище (процес) на мові математики. У свою чергу, в процесі побудови моделі можна виділити кілька кроків.

Перший крок – індуктивний: це відбір спостережень, що відносяться до того процесу, який належить моделювати. Цей етап полягає у формулюванні проблеми, тобто у прийнятті рішення щодо того, що слід брати до уваги, а чим можна знехтувати.

Другий крок полягає в переході від визначення проблеми до власне побудови неформальної моделі. Неформальна модель – це такий опис процесу, який здатний пояснити відібрані нами спостереження, але при цьому визначений недостатньо суворо, і не можна з точністю перевірити ступінь логічної взаємопов’язаності в ньому властивостей. На цій стадії розглядаються цілий ряд наборів неформальних допущень, здатних пояснити одні й ті ж дані; тим самим розглядаються декілька потенційних моделей і вирішується, яка з цих моделей найкраще відображає досліджуваний процес. Інакше кажучи, шукаються різні способи встановлення логічної відповідності між моделлю і реальним світом.

Третій крок – це переклад неформальної моделі в математичну модель. Такий переклад включає в себе розгляд словесного опису неформальної моделі та пошук підходящої математичної структури, здатної відобразити процеси, що вивчаються. Це найскладніший етап у всьому процесі моделювання.

Стадія перекладу може таїти в собі дві небезпеки. По-перше, неформальні моделі мають тенденцію бути неоднозначними, і зазвичай існує кілька способів перекладу неформальної моделі в математичну (при цьому альтернативні математичні моделі можуть мати абсолютно різний зміст). Насправді, це одна з головних причин, які спочатку штовхають до застосування математичних моделей: мова математики позбавлена двозначностей і більш точна, ніж природна мова, вона дозволяє досліджувати прихований сенс найтонших відмінностей у формулюваннях, який погано доступний дослідженню за допомогою природної мови.

Наступний етап – етап розв’язання задачі в рамках математичної теорії – можна ще назвати етапом математичної обробки формальної моделі. Він є вирішальним у математичному моделюванні. Саме тут застосовується весь арсенал математичних методів – логічних, алгебраїчних, геометричних і т. д. – для формального виведення нетривіальних наслідків з вихідних припущень моделі. На стадії математичної обробки зазвичай – незалежно від суті завдання – мають справу з чистими абстракціями і використовують однакові математичні засоби. Цей етап є дедуктивне ядро моделювання.

На останньому етапі моделювання отримані висновки проходять через ще один процес перекладу – цього разу з мови математики назад на природну мову.

Вчителеві слід домогтися від учнів чіткого розуміння значення і змісту кожного з вище описаних етапів процесу математичного моделювання. Це потрібно для того, щоб школярі засвоїли, що вони вирішують не просто математичну задачу, а конкретну життєву ситуацію математичними методами. Тоді учні зможуть побачити в математиці практичне значення і не будуть сприймати її як абстрактну науку.

Метод математичного моделювання є потужним інструментом для дослідження різних процесів і систем. Поняття математичної моделі і деякі загальні положення, пов’язані з ним, повинні в тій чи іншій формі ілюструватися протягом всього курсу математики, а розділи шкільної програми, присвячені задачам на роботу, рух, можуть розглядатися як введення в метод математичного моделювання.

Сучасні педагогічні ідеї, власні знахідки й напрацювання висвітлено в науково-методичних посібниках, підручниках, наукових статтях С.О.Скворцової, О.В. Онопрієнка І.М. Досяк, О.В. Полякової, у нормативних документах Міністерства освіти і науки України.

У чинній програмі з «Математики» визначені основні завдання для формування математичних компетенцій – обчислювальних, інформаційно-графічних, логічних, геометричних, алгебраїчних. Результатом засвоєння предметних компетенцій є математична компетентність учнів, яка виявляється в здатності розв’язувати сюжетні задачі, логічно міркувати, виконувати дії за алгоритмом, а також в умінні користуватися математичною термінологією, знаковою і графічною інформацією.

 

 

 

 

 

 

 

 

 

 

 

 

Опис власного досвіду

Актуальність застосування методу математичного моделювання  при розв’язуванні сюжетних задач зумовлюється невмінням учнями аналізувати умову задачі, що призводить до помилок при її розв’язанні. Викладаючи математику в початкових класах, я часто помічала, що  навіть учням, в яких добре сформовані обчислювальні навички, складно розв’язувати текстові задачі. Іноді це відбувається через недостатній життєвий досвід дитини, але частіше – через нерозуміння відношень між даними в задачі. Найефективнішим методом в аналізі задачі є моделювання. Навчання із застосуванням моделювання підвищує активність розумової діяльності учнів, допомагає зрозуміти завдання, самостійно знайти раціональний шлях розв’язання, встановити потрібний спосіб перевірки, визначити умови, за яких задача має чи не має розв’язки. Угорський математик Дьордь Пойа писав, що «навчання мистецтву розв’язувати задачі є вихованням волі учня, його наполегливості, терплячості».

Концепція «Нова  школа. Простір освітніх можливостей»  визначає, що компетентності – це динамічна комбінація знань, умінь, цінностей та ставлень на їхній основі, які визначають здатність особи успішно вирішувати життєві проблеми, провадити професійну і подальшу навчальну діяльність.

До ключових компетенцій, визначених у вказаному вище документі, відносять:

• спілкування державною мовою;
• спілкування іноземною мовою;
• математична грамотність;
• компетентності в природничих науках і технологіях;
• інформаційно-цифрові компетентності;
• уміння навчатися впродовж життя;
• соціальні і громадянські компетентності;
• підприємливість;
• загальнокультурна грамотність;
• екологічна грамотність і здорове життя.

Отож, важливе місце відведено формуванню математичної грамотності: уміння застосовувати математичні (числові та геометричні) методи для вирішення прикладних завдань у різних сферах діяльності, здатність до розуміння і використання простих математичних моделей, уміння будувати такі моделі для вирішення проблем.

Новизна власної методичної розробки передусім простежується в напрацюванні системи підготовчих вправ для ефективної реалізації можливостей методу математичного моделювання як важливого засобу активізації навчальної діяльності, формування думаючої особистості, яка може відстояти власну думку, знайти вихід з будь-якої ситуації.

Моделювання – важливий метод наукового пізнання і сильний засіб активізації учнів у навчанні. До основних цілей навчання математики належить формування умінь будувати математичні моделі найпростіших реальних явищ, досліджувати явища за заданими моделями, залучати учнів до досвіду творчої діяльності. В основі розв’язання сюжетних задач лежить математичне моделювання, тому необхідно застосовувати навчання  моделюванню з першого року навчання.

Практична значущість роботи полягає у формуванні в учнів здатності  розв’язувати сюжетні задачі, особливо практично зорієнтовані, із застосуванням методу математичного моделювання, забезпечуючи зв’язок математики із реальним життям дитини. Адже вміння розв’язувати задачі є показником навченості й научуваності, виявленням учнем своєї компетентності.

У початкових класах важливе місце посідають так звані сюжетні задачі. У них подаються значення величин і деякі залежності (відношення) між ними, причому ці залежності мають певні числові характеристики. Сюжетні задачі забезпечують зв’язок математики з реальним життям, впливають на формування світогляду молодших школярів, на удосконалення математичних вмінь і навичок та розвиток логічного мислення. Особливістю сюжетних задач є актуальність і доречність їх використання при підготовці різноманітних позакласних заходів, у роботі з обдарованими дітьми при підготовці до математичних олімпіад тощо. Підвищений інтерес в учнів викликають сюжетні задачі, з якими вони рідко, а то й зовсім не зустрічаються у підручниках, але які пов’язані з сьогоденням, містять нову для них інформацію. Це, наприклад, задачі економічного змісту: бюджет сім’ї, податки, робота банків, ведення фермерського господарства. Діти охоче розв’язують задачі природничого змісту, а часто і самі їх складають.

Вміння розв’язувати сюжетні задачі є найважливішим проявом математичної компетентності.

Достатньо далекими від математичної компетентності є запам’ятовування формул, уміння застосовувати готові схеми до розв’язання формальних задач. Математики треба вчити так, щоб учні могли знайти її застосування в повсякденному житті.

Пріоритетним принципом в навчанні математики повинні стати слова І. Канта: не треба заучувати думки, треба вчитися думати. Цьому повинні сприяти:

- розв’язування нестандартних задач, взятих з навколишньої дійсності, про знайомі речі і об’єкти;

- розв’язування задач різними способами.

Угорський математик Дьордь Пойа стверджував, що розв’язування задачі кількома способами дуже корисне, оскільки це підводить школярів до розуміння єдності світу. «Краще розв’язати одну задачу десятьма способами, ніж десять задач одним способом». Учень повинен зрозуміти зміст задачі і повинен хотіти її розв’язати, задача повинна бути цікавою. Інколи для розв’язання задачі треба учневі багато часу, цей шлях розуміння є звивистий. А інколи може бути миттєва блискавична ідея. Роль учителя – ненав’язливо допомогти знайти цю блискавичну ідею. 

Сюжетну задачу учневі легше розв’язати, коли він її змоделює, а саме: чітко уявить співвідношення між даними, величинами і зможе спрогнозувати результат, склавши для себе найраціональніший алгоритм. Розв’язану задачу треба аналізувати детально, ще раз проглядати розв’язок, а не швидко переходити до наступного завдання. У ході розв’язування задач здібний учень повинен побачити свої нахили, здібності, зрозуміти, що йому найбільше подобається. Так розкриваються таланти дітей.

Вміння розв’язувати сюжетні задачі є одним із головних показників рівня математичного розвитку дитини, засвоєння  нею навчального матеріалу. Випускник початкової школи повинен вміти коротко записувати умову задачі, ілюструючи її з допомогою малюнка, схеми чи креслення, пояснювати кожен етап в аналізі та розв’язанні, прогнозувати  і перевіряти результат.

Не всі учні люблять і вміють розв’язувати задачі. Це тому, що вони не навчені аналізувати дані, бачити взаємозв’язки між шуканими і даними, структурувати хід розв’язання. А при відсутності потреби в розумінні відношень, у дитини формується звичка зводити розв’язок до простого арифметичного обчислення.

Вдало організувати роботу над сюжетною задачею, залучити учнів до дослідної творчої діяльності, створити умови для усвідомлення ними матеріалу, розвивати самостійне свідоме мислення допоможе використання вчителем методу математичного моделювання.

Метод математичного моделювання наділений великою евристичною силою: дозволяє звести навчання складному і незнайомому до простого і знайомого, тому використання моделювання є ефективним засобом навчання. Як підтверджує практика, введення в зміст навчання понять «модель» і «моделювання» суттєво змінює ставлення учнів до математики, робить їх навчальну діяльність свідомою та продуктивнішою. А цілеспрямоване  і систематичне навчання моделюванню забезпечує інтелектуальний розвиток дітей. Для того, щоб «озброїти» учнів моделюванням як засобом пізнання, недостатньо вчителеві демонструвати створені моделі, треба домагатися того, щоб учні самостійно будували їх. Модель задачі дозволяє сформувати в кожного учня вміння розв’язувати задачу не після багаторазового вправляння в розв’язуванні однотипних задач, а за рахунок різнобічної творчої діяльності самого учня. Коли школяр, розв’язуючи сюжетну задачу, розуміє, що вона представляє собою знакову модель певної реальної ситуації, самостійно створює цю модель, обчислює її, дає повну відповідь мовою умови задачі, може перевірити розв’язання складанням оберненої задачі, тільки тоді можна стверджувати, що учень володіє методом математичного моделювання.

На уроках математики ці результати досягаються, якщо:

• вчити учнів працювати з текстом задачі: вибирати з нього математичні дані ( величини, зв’язки, відношення, залежності, числові дані);
• розробити свої знаки і символи;
• вчити школярів читати готові моделі і складати власні;
• складати до однієї задачі декілька моделей:
• складати за моделями обернені задачі.

В початкових класах школи формується ставлення дітей до навчання, яке вчитель може зробити цікавим і доступним. Використовуючи на уроках метод моделювання, учні зможуть не тільки зрозуміти задачу, але й знайти раціональний спосіб її розв’язання. В початковій школі можна ефективно використовувати такі види моделей:

• малюнок;
• предметна (знакова);
• графічна (креслення);
• схематична;
• репрезентативна (короткий запис);
• алгебраїчна (формули, рівняння);
• таблична (відношення);
• діаграмна (частини).

Більшість логічних задач  розв’язати можна лише методом моделювання.

Предметне і графічне моделювання математичних ситуацій при розв’язуванні задач давно використовується в шкільній практиці, але, на жаль, без відповідної і систематичної підготовки. Я навчаю першокласників математики за підручником Ф.М. Рівкінд та Л.В.Оляницької, де учні вперше зустрічаються із моделлю задачі, знайомлячись з поняттям «задача». Дітям, які швидко обчислюють в межах десяти, складно зрозуміти необхідність її використання (с.52). Тому в своїй роботі я практично готую учнів до свідомого моделювання з перших уроків. Мною розроблена система підготовчих вправ, які сприяють творчій діяльності учнів при розв’язуванні сюжетних задач.

Діти приходять до школи з певним багажем математичних знань, умінь та навичок, сформованих у дошкільний період. Уже на етапі узагальнення і систематизації цих знань, я готую їх до розв’язування задач. Учні повинні чітко розрізняти і порівнювати предмети за розміром, формою, кольором, встановлювати відношення між ними, пов’язані з їхньою довжиною, висотою, товщиною, розміщувати об’єкти на площині. Найефективніше застосовувати  для цього малювання, яке дає можливість кожному учневі безпосередньо бути учасником, а не спостерігачем на уроці.

 Малюнок – зображення реальних предметів, про які йде мова.

Для виконання малюнків я обираю предмети, які дітям добре знайомі і які легко можна намалювати. З метою формування свідомого ставлення і використання моделі у вигляді малюнка даю дітям такі завдання:

• намалювати одне велике зелене яблуко і два маленьких червоних так, щоб велике яблуко було справа;
• намалювати три ялинки, щоб кожна наступна була вищою за попередню;
• намалювати три м’ячі, щоб два з них були синього кольору, а найменший – червоного;
• намалювати чотири повітряні кульки так, щоб круглі були однакового кольору, але різного розміру, а овальні – однакового розміру, але різного кольору.

На одному з наступних уроків ми розглядаємо малюнок дитячого майданчика, на якому бавляться хлопчики та дівчатка. Я пропоную учням намалювати дітей, і ми стикаємося з «проблемою»: не всі можуть виконати це завдання. Тоді я пропоную намалювати стільки квадратиків, скільки на малюнку дітей. Учні успішно виконують це завдання. Але ми знову стикаємось з «проблемою»: як розпізнати кількість хлопчиків і дівчаток? Учні успішно знаходять відповідь: розфарбувати квадратики двома різними кольорами. Так ми наближаємося до предметного моделювання, а учні роблять висновок, що складні предмети можна замінити простими (найчастіше це геометричні фігури).

Уже на сьомому уроці учні знайомляться з геометричними поняттями: точка, пряма, ламана, крива, відрізок, промінь. Вони вчаться користуватися олівцем та лінійкою, ставити точки, креслити рівні відрізки, можуть на око порівнювати довжини відрізків. Щоб в учнів сформувати графічні навички, розвинути зорове сприйняття та логічне мислення, пропоную їм наступні завдання:

• поставте дві точки на аркуші паперу, а потім зігніть папір так, щоб точки стояли на лінії згину;
• поставте дві точки і проведіть через них пряму;
• поставте дві точки, з’єднайте їх;
• побудуйте два відрізки так, щоб перший був коротшим від другого;
• побудуйте один під одним три відрізки так, щоб два з них були рівні, а третій довший від двох інших;
• побудуйте відрізок, позначте на ньому точку так, щоб вона була розташована:
  • ближче до кінця відрізка, з’єднай її дужкою з кінцями відрізка;
  • посередині відрізка, з’єднай її дужкою з кінцями відрізка;
  • ближче до початку відрізка, з’єднай її дужкою з кінцями відрізка.

Коли учні навчаться охайно виконувати графічні завдання, можна знайомити їх з графічною моделлю. Дуже важливо навчити  дітей графічно позначати числа. Це доцільно демонструвати одночасно з використанням цифр та наочності при порівнянні чисел, ознайомлюючи учнів із знаками > ,<  та =.

Я викладаю на набірному полотні три грибочки, два горішки, два жолуді і один каштан і запитую :

– Скільки грибочків ви бачите? Якою цифрою позначимо число три?

– Скільки ви нарахували горішків? Якою цифрою позначимо число два?

– Якою цифрою позначимо кількість жолудів?

– Скільки каштанів?

– Чого більше? Чого менше? Чого порівну?

Знайомлю дітей із знаками, записуємо утворені нерівності. Потім пропоную учням побудувати відрізки так, щоб перший відповідав кількості грибочків, а другий – кількості горішків, третій – кількості жолудів, четвертий – каштанів і підводжу їх до висновку: більше число зображуємо довшим відрізком, а менше – коротшим, рівні числа позначаються однаковими відрізками.

 

 

Закріплюю  вміння графічно моделювати числа при вивченні дій додавання і віднімання. Об’єднуючи множини предметів, вчу дітей читати і записувати приклади на додавання, паралельно складаємо графічну модель дії додавання, яка допомагає учням побачити (позначаю кольоровою крейдою) та усвідомити, що в результаті додавання отримуємо більше число.

 …………………………..

 

Зображуючи графічно дію віднімання, даю завдання учням показати на графічній моделі результат дії віднімання самостійно , щоб переконатись, що в результаті віднімання завжди отримуємо менше число.

 ……………………………

 

Зручно використовувати графічні моделі дій додавання і віднімання при встановленні відношень між компонентами цих дій. Їх доцільно використовувати не етапі актуалізації опорних знань учнів, тоді діти  самостійно і свідомо сформулюють правила знаходження невідомого доданка, зменшуваного чи від’ємника.

   ……………………   або   …………………….  

 

   ……………………   чи   ………………………  

 

Графічне моделювання допомагає першокласникам уявити відношення «більше на», «менше на». Наприклад: олівець довший від ручки на 3см. Покажи графічно олівець і ручку. Познач відрізок, довжина якого 3см.

Ол.    ………………………

Р.       ……………….

Вивчаючи склад чисел першого десятка, я вчу дітей користуватись схематичною моделлю, яку в практиці часто використовую при аналізі складених задач. Наприклад:

 

 

                                                          

При вивченні переставного закону додавання першокласники вперше знайомляться з алгебраїчною (знаковою чи буквеною) моделлю.  Оскільки малюнок і предметне моделювання є найбільш зрозумілими для дітей, то саме їх я використовую для актуалізації опорних знань.

Складену рівність перетворюємо спочатку в знакову, зрозумілішу дітям, а потім в буквену модель. Наприклад:

 4 + 5 = 5 + 4 ,                                 , a + b = b + a.

 

Коли учні навчились будувати найпростіші моделі чисел, їх можна знайомити із моделями задач.

 

 

 

 

 

 

 

 

Результативність впроваджуваного

досвіду

Про результативність застосування методу математичного моделювання при розв’язуванні сюжетних задач у початкових класах свідчить постійне відстежування вмінь учнів розв’язувати задачі в кінці навчального семестру, що дає підставу стверджувати про рівень отриманих знань і вмінь школярів з математики.

 Розв’язування простих задач в 1 класі ( І семестр, ІІ семестр, підсумкова контрольна робота)

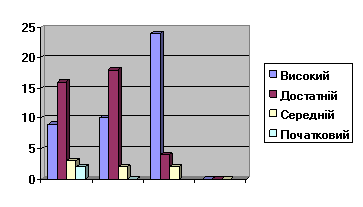
Розв’язування складених задач на 2 дії в 2 класі (І семестр, ІІ семестр)

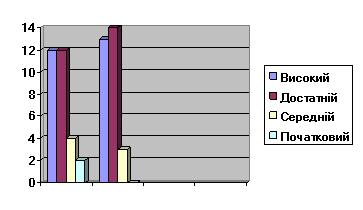
Розв’язування складених задач на 3 дії в 3 класі ( І семестр, ІІ семестр)

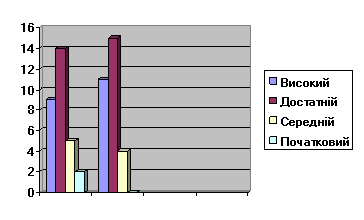
Розв’язування складених задач різними способами в 4 класі (І семестр, ІІ семестр)

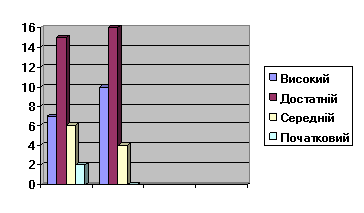
Розв’язування задач з логічним навантаженням .

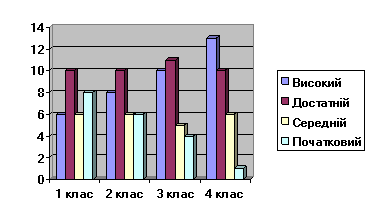
В процесі формування математичних компетентностей учнів відбувається формування обчислювальних навичок, глибокого розуміння відношень між величинами, розвиток логічного мислення, ціннісного ставлення до себе та людей.

Результати моєї роботи вказують на ефективність застосування засобів та методів навчання. Якість знань учнів з предмета «Математика» за підсумками  державної підсумкової атестації становить 96%. За результатами опитування, проведеного в класі, зазначений вище предмет є улюбленим у 73% учнів.

Важливе місце у моїй діяльності відводжу формуванню самоосвітньої компетентності, творчої, продуктивної діяльності з обдарованими дітьми або такими, що виявляють інтерес до вивчення математики. Учні класу, в якому я працюю, беруть участь у шкільних предметних олімпіадах, Міжнародному  конкурсі «Кенгуру». Учениці Бойко Лілія та Мотульська Вікторія були переможцями І (шкільного) етапу олімпіади з математики та гідно виступили на ІІ (міському) етапі. Скікун Богдан був призером І та ІІ етапів олімпіади з математики. Кардаш Данило, Серман Анастасія. Скікун Богдан і Яворська Ольга вступили до Калуської гімназії імені Дмитра Бахматюка.

Крім цього, мої учні є активними учасниками математичних вікторин, виховних заходів з математики. У першому класі учні презентували свої знання та вміння на святі Першого десятка. У третьому – змагались у математичному турнірі «Математика – цариця наук!» (Додаток)

Переконана, що досвід моєї роботи забезпечить формування освіченого українця, всебічно розвиненого, відповідального громадянина і патріота, здатного до інновацій, такого, котрий поведе українську економіку вперед у XXI столітті.

 

 

 

 

 

 

 

 

 

Методичні рекомендації

щодо застосування

методу математичного моделювання 

 при розв’язуванні сюжетних задач

 в початкових класах

 Розв’язування простих задач

 методом математичного моделювання

Знайомство із задачами першокласники розпочинають із простої задачі на знаходження суми. Я розповідаю дітям, що задача – це цікава історія або розповідь. Але не кожна розповідь чи історія є задачею! Лише тоді, коли вони мають запитання, вони утворюють задачу. Я завжди наголошую учням, що  задача не є загадкою, яку треба відгадати, а є реальною життєвою ситуацією, котру потрібно уважно проаналізувати і розв’язати математичним обчисленням, і обов’язково відповісти на її запитання. Під математичною задачею розуміють будь-яку вимогу: знайти, обчислити, побудувати, дослідити. Учні дізнаються, що задача складається з умови, запитання, розв’язання та відповіді.

Щоб краще засвоїти структуру задачі пропоную учням такі завдання.

• Придумай запитання до задачі:

У вазі було 5 цукерок, мама поклала ще 3.

Оля вирізала 3 сніжинки, а Іринка – 2 сніговички.

• Придумай умову до запитання задачі:

Скільки всього цукерок стало у вазі?

Скільки новорічних прикрас вирізали Оля і Іринка разом?

Аналізуючи умову задачі, учні в парах самостійно будують предметну модель задачі за допомогою геометричних фігур, які обирають на власний розсуд. Я контролюю цей процес, коригуючи, при потребі, кількість обраних множин. Якщо в задачі мова йде тільки про цукерки, то при моделюванні задачі логічно обрати однакові фігури (трикутники або кружечки). Для моделювання другої задачі учням необхідні і трикутники, і кружечки. Предметне моделювання задач дітям дається легко. Я пропоную скласти свою задачу за утвореними моделями.

Наступним етапом буде складання графічної моделі до цих самих задач.

Оскільки діти вправлялись у графічному моделюванні чисел та дії додавання, вони свідомо складають моделі до задач під керівництвом вчителя.

Наприклад:       …………………      та     ……………….. .

 

Діти можуть пояснити графічну модель, подану в підручнику (с.53), скласти задачу за такою моделлю.

При розв’язанні задач на знаходження суми я показую учням, що дані задачі можна записати і в схематичну модель, котру вони заповнювали при вивченні складу чисел. Наприклад:     

 

 

Короткий запис задачі є репрезентативною моделлю задачі, і його складання передбачає дії кодування тексту задачі. Вчити складати короткий запис потрібно паралельно з іншими видами моделювання задачі. Для цього учні повинні вміти визначати «головні слова» в тексті задачі. Це можуть бути персонажі задачі, види предметів або послідовність дій. Складемо короткий запис до розв’язуваних нами задач.

Було – 5 ц.                                                     Було – 5 ц.

Поклала – 3 ц.                            або             Поклала – 3 ц.

Стало –  ? ц.

Другим видом задач, які вивчають першокласники, є задачі на знаходження остачі. Ці задачі теж зрозумілі дітям. У ході їх вивчення можна використовувати перераховані вище моделі.

Задача. На гілці сиділо 6 пташок. Дві пташки полетіли. Скільки пташок залишилось?

Предметна модель:

Графічна модель:      …………………………   (с.54)

Схематична модель:

 

 

Репрезентативна :         Сиділо – 6 пт.

                                        Полетіли – 2 пт.

                                        Залишилось – ? 

Отже, при розв’язуванні простих задач на знаходження суми та остачі першокласників треба вчити складати предметну, графічну, схематичну та репрезентативну моделі, а не зводити розв’язання задач до виконання арифметичного обчислення. 

Задачі на збільшення чи зменшення числа на кілька одиниць засвоюються учнями легко на основі сформульованого  в підручнику правила. Учні, володіючи методами графічного та предметного моделювань, самостійно будують моделі таких задач, складають задачі за поданими моделями (с.62)

Задачі на знаходження невідомого доданка є оберненими задачами до задач на знаходження суми. Вже на цьому етапі навчання я знайомлю учнів з поняттями «пряма» і «обернена» задача. У практичній діяльності, опираючись на досвід учнів складати графічну, схематичну та репрезентативну моделі до задачі, робимо висновок, що обернених задач можна скласти стільки, скільки є числових даних у прямій задачі.

Наприклад: На галявині бігало 3 зайчики, до них прибігло ще 2. Скільки всього зайчиків стало на галявині?(с.66)

   …………………            Було        –3 з.

                                           Прибігло – 2 з

                                           Стало       – ? з.

Складемо обернену задачу № 1

   …………………            Було         – ? з.

                                           Прибігло  – 2 з.

                                           Стало        – 5 з.

Складемо обернену задачу № 2

   …………………            Було          – 3 з.                       

                                           Прибігло   – ? з.

                                           Стало         – 5 з.

Аналогічно, опираючись на вміння учнів будувати моделі до задач на знаходження остачі, вчу першокласників розв’язувати задачі на знаходження невідомого зменшуваного чи від’ємника. Закріплюю вміння складати обернені задачі.

Задачі на різницеве порівняння особливо потребують детального аналізу, бо часто учні, знаючи  правильну відповідь, затрудняються у складанні дії для розв’язання задачі (с.74).

Наприклад: В одній коробці 6 олівців, а в іншій – 9. У якій коробці більше олівців і на скільки? Побудуємо спочатку предметну модель задачі, на якій чітко видно, в котрій коробці більше олівців. Щоб показати «на скільки більше» пропоную учням обвести ці олівці червоним кольором:

І І І І І І

І І І І І І І І І

Перейдемо від предметного моделювання до графічного:

……………..

……………………..

 

Позначте червоним кольором частину відрізка, яка показує «на скільки більше олівців у другій коробці».

Першокласники роблять висновок:  отримали менше число.

Аналогічно розглядаємо цю ж задачу, змінивши до неї запитання: на скільки менше олівців у першій коробці? Учні самі роблять висновок, який підтверджуємо правилом із підручника. Щоб дізнатися, на скільки одне число більше або менше за інше, треба від більшого числа відняти менше. Тільки після аналізу умови задачі засобами предметного і графічного моделювання, доцільно ознайомлювати учнів з коротким записом умови задачі даного виду.

В І к. – 6 ол.

В ІІ к. – 9 ол.

Особливої уваги потребують задачі з непрямим змістом, котрі містять поняття «це більше на» або «це менше на». Для усвідомлення правильного вибору арифметичної дії при розв’язуванні таких задач, я пропоную учням проаналізувати графічні моделі задач, які обчислюються  однаковими діями. Наприклад. Прочитайте задачі. Що в них однакове? Складіть графічні моделі задач і порівняйте їх. Якою арифметичною дією ви розв’яжете ці задачі? Чим відрізняються умови задач?

Задача 1. Для приготування салату мама взяла 8 помідорів, а огірків – на 3 менше. Скільки огірків для салату взяла мама?

 

     ………………………………

     …………………

Задача 2. Для приготування салату мама взяла 8 помідорів, це на 3 більше, ніж огірків. Скільки огірків для салату взяла мама?

 

     ………………………………..

     …………………..

Учні роблять висновок, що обидві задачі розв’язуються дією віднімання. Щоб закріпити знайомство із задачами з непрямим змістом, я пропоную учням скласти і розв’язати задачу за малюнком (с.70). Скласти самостійно задачі з непрямим змістом, які б розв’язувались дією віднімання.

Після того, як учні другого класу ознайомляться з рівнянням, вони вчаться складати алгебраїчну модель для розв’язування простих сюжетних задач на знаходження компонентів арифметичних дій додавання та віднімання (сс.14,18,19). З практики хочу відмітити, що розв’язувати задачі рівнянням учням легко. Другокласники швидко усвідомлюють зміст задачі, легко позначають буквами або знаками шукане (невідоме) число. Користуючись складеним рівнянням, учні складають обернені задачі.

Головне завдання вчителя на цьому етапі навчання допомогти дітям скласти умову та запитання до оберненої задачі. Наприклад, розв’яжи задачу за допомогою рівняння, склади обернену.

Задача. На Сорочинський ярмарок гончар привіз 7 куманців і декілька глечиків. Скільки глечиків привіз гончар на ярмарок, якщо всього посуду було 15 предметів.

х – кількість глечиків;

7 + х = 15

х = 15 – 7

х = 8

Відповідь: гончар привіз 8 глечиків.

Обернена задача

х – кількість куманців;

х + 8 = 15

х = 15 – 8

х = 7

Відповідь: гончар привіз 7 куманців.

У другому семестрі другокласники знайомляться із дією множення як додаванням однакових доданків, а також вчаться розв’язувати прості задачі на конкретний зміст дії множення. При аналізі таких задач спочатку учні користуються малюнком, потім будують графічні моделі, а згодом вчитель знайомить їх із особливістю репрезентативної моделі.

Наприклад: В одній пляшці 2 л соку. Скільки літрів соку в 3 таких пляшках? (с.92)

 

………………………….                      По 2 л взяли 3 рази – ? л

 

Розв’язання: 2 + 2 + 2 = 6, отже 2 · 3 = 6 (л)

 

Користуючись графічною схемою та коротким записом учні вчаться розв’язувати задачі на збільшення у рази.

Дію ділення учні вивчають аналізуючи умову задач, котрі розкривають конкретний зміст ділення на рівні частини та на вміщення (с.97-98).

Найефективнішим засобом аналізу в цьому випадку є малюнок, який дозволяє учням побачити відмінність ділення на рівні частини від ділення на вміщення. Також доцільно виконати предметне моделювання, в якому діти взяли б безпосередню участь. І тільки тоді я пропоную школярам скласти графічну модель задачі та знайомлю їх з особливістю короткого запису цього виду задач.

Задача 1. Мама розклала 8 цукерок на тарілки по 2 на кожну. Скільки тарілок використала мама?

 

   …………………………….    8 ц. поділити по 2 ц. – ? т.

 

Задача 2. Мама розклала 8 цукерок на 2 тарілки порівну. Скільки цукерок поклала мама на кожну тарілку?

 

   …………………………..   8 ц. поділити на 2 т. порівну – ? ц.

 

Діти роблять висновки, що розв’язання задач записується однаково. Особлива увагу учнів звертаю на ключове слово у запитанні і вчу давати правильну відповідь на запитання задачі.

Коли учні другого класу навчаться розв’язувати рівняння на знаходження компонентів дій множення та ділення, я пропоную їм алгебраїчну модель для розв’язування таких задач, вчу складати обернені задачі (с.120).

 

Наприклад: Для гри учнів класу поділили на 4 команди. Скільки дітей у кожній команді, якщо у класі 28 учнів?

х – кількість учнів в одній команді;

х · 4=28

х = 28 : 4

х = 7

Відповідь: 7 учнів у кожній команді.

Обернена задача

х – кількість команд;

7 · х = 28

х = 28 : 7

х = 4

Відповідь: учнів поділили на 4 команди.

Прості задачі на кратне порівняння найкраще розпочинати з аналізу короткого запису цих задач, який підкріплюється малюнком, порівнюючи його із коротким записом задачі на різницеве порівняння. Я пропоную учням знайти відмінності, пригадуємо значення понять «більше на», «більше у рази», опрацьовуємо правило на с.132. Сильніші школярі складають задачі за короткими записами на с.133.

У третьому класі учні вивчають прості задачі, що містять пропорційні величини і знайомляться із табличною моделлю, яку використовують для аналізу тексту задачі. Школярі вчаться також складати задачі за даними в таблиці.

 

Продуктивність праці ( за 1 день)	Час роботи	Загальний виробіток
?	5 днів	35 серветок
4 футболки	?	28 футболок
9 деталей	4 дні	?

 

Ціна	Кількість	Вартість
8 грн	5 кг	?
10 грн	?	60 грн
?	3 шт.	27 грн

 

Прості задачі на знаходження частини від числа та числа за числовим значенням його частини третьокласники вивчають у другому семестрі.

Діти часто чують від старших слова «півкілограма яблук», «третя частина, кавуна», «чверть години» тощо. Цей життєвий досвід учнів треба впорядкувати і систематизувати. Правильні уявлення про частини, а пізніше про дроби будуть сформовані тоді, коли діти своїми руками зроблять, наприклад, половину круга, знайдуть четверту частину смужки, тим самим користуючись матеріальними моделями. Перегинаючи круг, смужку паперу навпіл, діти роблять висновок, що половини одного й того самого круга чи тієї самої смужки паперу рівні між собою. На цьому самому уроці вони розглядають малюнок або діаграму.

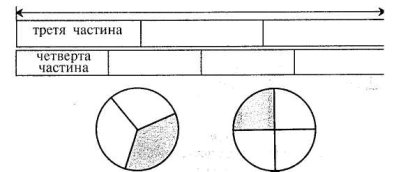
Перша смужка поділена на 3 рівні частини, а друга — на 4. Знайдіть, чому дорівнює третя і четверта частини смужки. Третя частина ще називається третина, а четверта — чверть. Покажіть на малюнках третю і четверту частини круга.

 

Задача 1. Знайдіть половину, третину і чверть числа 12.

Задача 2. Четвертина числа дорівнює 3. Знайдіть це число.

У четвертому класі учні розв’язують прості задачі з величинами швидкість, відстань і час, вчаться будувати і читати табличні моделі.

 

Назва	Швидкість	Час	Відстань
Велосипедист	10 км/год	3 год	?
Автомобіль	36 км/год	?	72 км
Теплохід "Комета"	?	4 год	280 км

 

 

Складаючи з учнями  на уроках математичні моделі до задач,  вчитель може проводити різноманітну творчу роботу, яка допомагає школярам полюбити математику, розвиває уяву та логічне мислення дітей. Я часто знайомлю учнів з різноманітними професіями, ми розмірковуємо над тим, де і як застосовують знання математики продавці, будівельники, лікарі і т. д. Учні, працюючи в групах, обирають професію і за даною моделлю складають інтегровані задачі.

Наприклад,

Продуктивність праці	Час роботи	Загальний виробіток
?	3 год	12

 

1 група. Перукарі. За 3 год перукар підстриг 12 хлопчиків. Скількох хлопчиків підстригає перукар за 1 год?

2 група. Швачки. За 3 год швачка пошила 12 фартушків. Скільки фартушків шиє швачка за 1 год ?

3 група. Гончарі. За 3 год гончар виготовив 12 глечиків. Скільки глечиків виготовляє гончар за 1 год?

Розв’язування складених задач

методом математичного моделювання.

Задачу називають складеною, якщо для її розв’язування треба виконати дві і більше взаємопов’язаних арифметичних дій. Задачі на дві дії вводяться у другому класі. Вид складеної задачі визначається видами простих задач, які до неї входять.

Задача. На столі лежало 5 яблук і 3 груші. За обідом 4 фрукти з’їли. Скільки фруктів лишилося на столі?

Вид задачі: на знаходження суми двох чисел, на знаходження остачі (різниці) двох чисел.

Розглянемо особливості роботи на складеною задачею:

■ сприймання тексту задачі зі слів вчителя чи самостійно;

■ пояснення незнайомих термінів;

■ перевірка усвідомлення змісту задачі (виділення умови і запитання, пояснення того, про що йде мова в задачі, на що вказує те чи інше число, з’ясування, що було на початку події, в кінці і т.д.;

■ складання математичної моделі задачі;

■ вербальний (словесний) розбір задачі здійснюється  синтетичним (від числових даних до запитання) або аналітичним (від запитання до числових даних) способом.

Суть синтетичного способу розбору задачі полягає у тому, що з сукупності числових даних складеної задачі вибираємо одну пару чисел і до неї ставимо відповідне запитання. Потім беремо другу пару чисел (одне з даних вже може бути результатом першої дії) і добираємо відповідне запитання. Таким чином, утворюються наступні прості задачі. В останній простій задачі ставиться основне запитання складеної задачі. Число, яке дістали внаслідок розв’язання останньої простої задачі, є відповіддю на запитання складеної задачі.

Особливість аналітичного способу в тому, що спочатку визначають необхідні прості задачі (складають план розв’язування), а вже потім розв’язують.

Слід звернути увагу на те, що на етапі аналізу задачі арифметичні дії не виконуються, операції з числами не відбуваються. Кожен із розглянутих способів словесного розбору задачі має позитивні і негативні сторони. Синтетичний спосіб легший для дітей. Аналітичний спосіб гарантує правильне розв’язання задачі, він більш цілеспрямований щодо складання плану розв’язування задачі, але для задач на три і більше дій він громіздкий. Не виключене також застосування аналітико-синтетичного прийому.

Оформляючи розв’язання задачі у зошиті учні подають повне пояснення знайдених числових даних у разі, якщо план розв’язування у зошит не записувався.

Основними способами перевірки є: співставлення даних з отриманим результатом.

Повний аналіз і графічне зображення складеної задачі

Задача. Купили 40 кг помідорів. Восьму частину маси усіх помідорів залишили для їжі, а решту засолили порівну в 7 банок. Скільки кілограмів помідорів поклали в кожну банку?

Що треба знати, щоб відповісти на запитання задачі? (Треба знати, скільки банок було і скільки кілограмів помідорів засолили). Скільки банок було — відомо, а скільки кілограмів помідорів засолили — невідомо.

 Що треба знати, щоб знайти, скільки всього засолили помідорів? (Треба знати, скільки кілограмів помідорів купили і скільки залишили для їжі). Скільки кілограмів помідорів купили — відомо, а скільки залишили для їжі — невідомо.

 Що треба знати, щоб знайти, скільки кілограмів помідорів залишили для їжі? (Треба знати, скільки всього кілограмів помідорів купили і яку частину їх залишили для їжі. Обидві величини відомі).

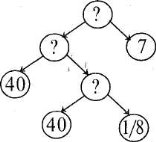Повний аналіз задачі графічно зображено на схематичній моделі.

 

 

 

 

 

Кружечки зі знаком запитання позначають головне і проміжні запитання задачі. Від кожного з них проведено дві стрілки. В кінці стрілок у кружечках записують числа (відомі або невідомі), необхідні для знаходження відповіді на запитання.

Зауважу,  що при відшуканні способу розв’язування від числових даних до запитання графічне зображення буде мати такий вигляд, як показано на схемі нижче.

 

 

 

 

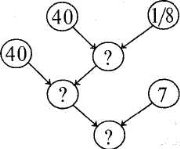
Відповідно до проведеного аналізу план розв’язування задачі буде такий.

1) Скільки кілограмів помідорів залишилося для їжі?

2) Скільки кілограмів помідорів засолили в банках?

3) Скільки кілограмів помідорів поклали в кожну банку?

Способом повного аналізу задачі з його графічним зображенням доцільно розв’язувати задачі в 3-4 класах під керівництвом учителя. Для самостійної роботи молодшим школярам я пропоную готові моделі, котрі допомагають їм у самостійному пошуку розв’язання задачі.

 

Наведу зразки табличних моделей складених задач.

Задача. З 14 м полотна пошили 7 наволочок. Скільки таких наволочок можна пошити з 8 м полотна?

 

Норма на одну наволочку	Кількість наволочок	Кількість тканини
Однакова	7 ?	14 м 8 м

Задача. На 45 грн купили набори олівців ціною по 5 грн. Стільки ж купили наборів фарб ціною по 8 грн. Скільки грошей заплатили за набори фарб?

Назва	Ціна	Кількість	Вартість
Набори олівців	5 грн	Однакова	45 грн
Набори фарб	8 грн		?

 

Розв’язування складених задач двома способами за допомогою

графічно-схематичної моделі

Задача. З двох міст одночасно назустріч один одному виїхали велосипедист і мотоцикліст, які зустрілися через 3 год. Швидкість велосипедиста дорівнює 12 км/год, а мотоцикліста — 50 км/год. Яка відстань між містами ?

Прочитавши умову задачі спочатку визначаємо учасників та напрямок руху. Учні самостійно будують графічну модель, детально проаналізувавши умову задачі. Можна виконувати це завдання в групах.

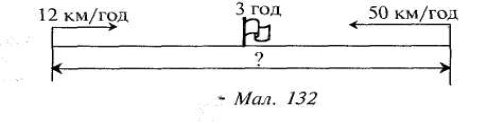
Аналіз проводимо від числових даних. Що відомо про рух велосипедиста? (Швидкість і час руху). Про що звідси можна дізнатися? (Про відстань, яку проїхав велосипедист до зустрічі). Що відомо про рух мотоцикліста і що можна знайти? (Відомі швидкість і час, можна знайти відстань). Чи можна знайти відстань між містами?

Складаємо план розв'язування задачі і записуємо розв’язання.

1) 12 · 3 = 36 (км) — проїхав велосипедист;

2) 50 · 3 = 150 (км) — проїхав мотоцикліст;

3) 36 + 150 = 186 (км) — відстань між містами.

Проаналізувавши розв’язання я звертаю увагу учнів на те, що задачу можна розв’язати іншим способом. Шукаємо другий спосіб розв’язування задачі. Велосипедист і мотоцикліст рухалися 3 год. Чи можна знайти, на скільки кілометрів зближувалися велосипедист і мотоцикліст за одну годину? (Можна. Для цього треба додати відстані, які подолали за годину окремо велосипедист і мотоцикліст).

Велосипедист і мотоцикліст зближувалися 3 год. Як знайти відстань, яку вони подолали за цей час?

1) 12 + 50 = 62 (км/год) — швидкість зближення велосипедиста і мотоцикліста;

2)  62 · 3 = 186 (км) — відстань між містами.

Підсумовуючи розв’язання задачі другим способом, я звертаю увагу учнів на те, що він є раціональнішим, підводжу їх до думки, що при русі в протилежних напрямках можна знаходити швидкість віддалення.

 

Математичні моделі задач можна використовувати і при тестовій перевірці знань учнів.

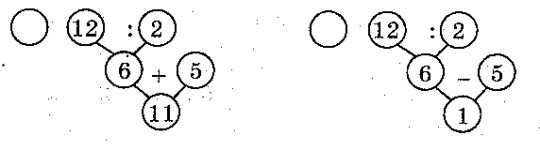
Задача. Дві дівчинки разом знайшли 12 грибів, порівну кожна. А хлопчик знайшов на 5 грибів більше, ніж одна дівчинка. Скільки грибів знайшов хлопчик?

Вибери схему розв’язання задачі.

Розв’язування логічних задач

методом математичного моделювання

Надзвичайно ефективно застосовувати метод математичного моделювання при розв’язуванні логічних задач. Як відомо, більшість із них пояснити учням можна тільки за допомогою малюнків, креслень, схем, таблиць  чи рівнянь. Розглянемо, як  можна використати графічне моделювання при розв’язанні логічних задач.

Задача. Миколка вищий за Василька, але нижчий за Гліба. Хто вищий – Василько чи Гліб?

 М. ………………………

 В.  …………………….

 Гл. …………………………….

 Складена  модель наочно продемонструє учням, що Гліб вищий за Василька.

 Задача. Бегемот важчий за носорога, ведмідь легший за носорога, а слон важчий  за бегемота. Хто з тварин найважчий?

 Б.  …………………………..

 Н.  …………………….

 В.  ………………

 Сл. ………………………………….

 Відповідь: найважчий слон.

 Задача. Петрик із Сергійком стоять в черзі за квитками. Петрик стоїть  третій від каси, а Сергійко – третій з кінця. Чи стоять хлопчики поряд, якщо в черзі 4 осіб? Хто першим купить квиток?

 ……………С……П……………………..

 Відповідь: хлопчики стоять поряд, Сергійко першим купить квиток.

 Задача. Оленка з мамою подорожує потягом. Дівчинка порахувала, що вони сіли у 2 вагон спочатку, але в 5 вагон з кінця потяга. Скільки вагонів у потязі?

 ………………………………………..

 Відповідь: 6 вагонів у потязі.

 Задача. На алеї посадили 10 каштанів через 5 м. Яка відстань між крайніми деревами?

 

 …………………………………………………..

5 · 9 = 45 (м)

 Відповідь: 45 м між крайніми деревами.

Задача. У Оленки, Ніни та Марини разом 20 ляльок. У Олени на 5 ляльок більше, ніж у Ніни, а у Ніни – на 3 менше, ніж у Марини. Скільки ляльок у кожної дівчинки?

О. ……………………………

Н. …………….........     20

М. ………………………..

1) 20 – 5 – 3 = 12 (л.) – разом, але порівну в кожної дівчинки;

2) 12 : 3 = 4 (л.) – у Ніни;

3) 4 + 3 = 7 (л.) – у Марини;

4) 4 + 5 = 9 (л.) – у Оленки.

Відповідь: у Оленки 9 ляльок, у Маринки – 7 ляльок, а в Ніни – 4.

Задача. В Оленки, Софійки і Марічки в коси заплетені стрічки червоного, блакитного і зеленого кольорів. Якого кольору стрічка у кожної дівчинки, коли відомо, що в Оленки не червона, у Софійки не блакитна, а в Марічки не червона і не зелена?

	червоний	блакитний	зелений
Оленка	–		+
Софійка	+	–
Марічка	–	+	–

 

Очевидно, що слід посилювати практичний, прикладний характер освіти, у тому числі предметного навчання, і урізноманітнювати роль учителя, який повинен бути не стільки наставником, скільки організатором навчально-пізнавальної діяльності школярів на уроці. Сучасному вчителю потрібно будувати свою роботу так, щоб кожен школяр знаходив задоволення від навчання, щоб зростав щодня. Учень молодших класів здатний робити маленькі відкриття: «Я можу! Я зумів!» Але потрібно пам’ятати, що успіх відкриття не може з’явитись на порожньому місці. Його потрібно довго і терпляче готувати. Дитину слід переконувати, що вона може досягти успіху, що в неї досить і сили, і розуму, що успішності вона, насамперед, зобов’язана собі. Допомога вчителя, якою б ефективною вона не була, повинна бути потайною.

 

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

 

 

 

 

 

 

 

 

 

 

 

1. Державний стандарт початкової загальної освіти [Електронний ресурс] // Постанова Кабінету Міністрів України від 20 квітня 2011 р. № 462 Київ. – 2011. – Режим доступу до ресурсу: http://mon.gov.ua/activity/education/zagalna-serednya/derj-stand.html.

2. Оновлені навчальні програми початкової школи. – 2016.

3. Концепція «Нова школа. Простір освітніх можливостей».

4. Актуальні проблеми методики навчання математики: Матеріали регіональної наукової  практичної  конференції, 2008 рік. – О.: Наука і техніка, 2008. – С. 128-136.

5. Богданович М., Козак М., Король Я. « Методика викладання математики в початкових класах». Навчально-методичний посібник. – К.,1999.

6. Досяк І. М. Нестандартні уроки з використанням інноваційних технологій.1–  4 класи. – Х.: Основа, 2007. – 160 с.

7. Жменька, А. Б. Зустрітися з математичним моделюванням [Текст] / А.Б. Жменька. – М.: Знание, 1991. - 160 с.

8. Мельничук Л. Моделювання життєвих і проблемних ситуацій (формування математичної компетентності) / Електронний ресурс. Режим доступу // http://ukped.com/predmetni-metodiki/matematika2/6041-modelyuvannya-zhyttyevykh-i-problemnykh-sytuatsiy-formuvannia-matematychnoi-kompetentnosti.html

9. Онопрієнко О.В. Предметна математична компетентність як дидактична категорія / О.В. Онопрієнко // Початкова школа. – 2010. – №11. – С.47–49.

10. Полякова О.В. Компетентнісний підхід у навчанні математики учнів початкової школи // Електронний ресурс. Режим доступу // http://teacher.at.ua/publ/19-1-0-1655

11. Пойа Д. Как решать задачу. – М., 1959. – 208 с.

12. Скворцова С.О. Методика навчання розв’язування сюжетних задач у початковій школі. – Одеса. ООО «Абрикос Компани», 2011. – 264 с.

13. Скворцова С.О., Онопрієнко О.В. Новації у навчальній програмі з математики для 1-го класу: шляхи реалізації / О.С.Скворцова, О.В.Онопрієнко // Початкова школа. – 2012. – №10.

14. Уйомов, А. І. Логічні основи методу моделювання [Текст] / А. І. Уйомов. – М.: Просвещение, 1996.

15. Філер З.Ю., Фадєєва Т.О. Формування алгоритмічності мислення молодших школярів // Початкова школа. – 2008. – № 2. – С. 52 – 56.

16. Фрідман, Л. М. Наочність та моделювання в навчанні [Текст] / Л. М. Фрідман. – М.: Знание, 1984. – 80 с.

17. Хуторской А. Компетентность как дидактическое понятие: содержание, структура и модели конструирования // http://khutorskoy.ru/books/2008/A.V.Khutorskoy_L.N.Khutorskaya_Compet.pdf

18. Штофф В. А. Моделювання і філософія [Текст] / В. А. Штофф. – М.: Наука, 1966.

 

 

 

 

 

 

 

 

 

 

 

 

Додатки

 

 

 

 

 

 

 

 

 

 

Конспект

 уроку математики

в 2 класі

 

 

 

 

 

 

 

 

Тема. Додавання та віднімання числа 7 з переходом через десяток. Складання і розв’язування задач за схемами. Побудова прямокутника. Знаходження його периметра.

Мета.

• Формування предметних компетентностей: актуалізувати знання учнів про склад числа 7, розвивати вміння доповнювати одноцифрове число до 10, вдосконалювати вміння складати  та розв’ярзувати задачі за схемами, будувати прямокутники із зазначеними сторонами, знаходити їх периметр; розвивати критичне мислення, вміння виділяти головне.
• Формування  ключових компетентностей:
  • вміння вчитись: розвивати вміння організовувати своє робоче місце, планувати власні дії, оцінювати свою роботу та діяльність однокласників, розвивати пізнавальний інтерес;
  • комунікативної: розвивати математичне мовлення, вміння доводити власну думку, правильно формулювати висловлювання з використанням математичних термінів;
  • соціальної: розвивати вміння продуктивно працювати в парах, групах, виявляти ініціативу, докладати власних зусиль для досягнення спільного результату;
  • громадянської: розширити знання учнів про гриби,розвивати вміння розрізняти їстівні та отруйні гриби, виховувати дбайливе ставлення до природи.

Тип уроку: комбінований.

Основні терміни і поняття: склад числа, графічна модель задачі, обернена задача, периметр.

Міжпредметні зв’язки : природознавство, літературне читання.

Обладнання : таблиці і картки із завданнями, «світлофори», загадки. Презентація  «Істівні і отруйні гриби».

 

Хід уроку

І, ВСТУПНА ЧАСТИНА

1. Організація класу

Сядьте , діти, всі гарненько,

Усміхніться всі миленько.

Настрій на урок візьмемо

Й працювати розпочнемо

2. Актуалізація опорних знань

Усні обчислення

• Обчислення виразів з буквеними даними ( фронтальна робота)

а	8 + а	11 –  а	7 + а	12  –  а
3
6

 

• Розв’язування задачі ( робота в малих групах )

Петрик знайшов 8 грибів, а Івась – на 6 грибів більше. Скільки грибів знайшов Івась?        ( 8 + 6 = 14 ( гр..) )

 

•   Читання тексту загадки з пропущеними буквами.

В т-пл-й  д-щ-к  н-р-д-л-сь,

П-р-с-льк-м-  н-кр-л-сь.

М-ж-  б  з  л-с-  п-стр-б-л-,

Якб-  др.-г-  н-г-  м-л-. (Гриби)

– Що ви знаєте про гриби? До якої природи належать ? Це рослини чи тварини? Якими бувають гриби?

    Перегляд презентації «Істівні і отруйні гриби»

– Відгадайте загадки

Зі своїх найперших днів

Найбіліший із грибів.

По властивостях він цінний.

Лікар від хвороб безцінний.(Білий гриб)

Красень гриб цей хоч куди,

Та у руки не бери!

Кожна муха його знає,

Та побачить, геть втікає! (Мухомор)

 

• Запис та обчислення значень виразів, які записані на малюнках їстівних грибів ( робота в парах зі самоперевіркою з дошки)

 

Каліграфічна хвилинка

– Відгадайте загадку.

Кількість днів тижня позначаю,

І кольори перелічую.

Всі ноти в музиці я знаю,

Себе «магічним» називаю. (7)

– Пригадайте, що ви знаєте про це число? (фронтальне опитування з використанням прийому «Мікрофон»)

Цифра сім, мов кочерга,

В неї лиш одна нога.

Фізкультхвилинка

Письмо цифри 7 носиком, вушком, ліктем, коліном

 

– Напишіть один рядочок цифри 7 і обведіть зеленим олівцем найкрасивішу!

–  Пригадайте склад числа 7 ( за таблицею)

– Назвіть «сусідів» числа 7  ( за натуральним рядом чисел)

 

ІІ. ОСНОВНА ЧАСТИНА

1. Повідомлення теми і мети уроку (з використанням методу «Мозковий штурм»)

– Подивіться, будь ласка, на таблицю, що ви помітили?

8 + 7 = 15

15  – 7 = 8

 

– Що нам потрібно пригадати, щоб виконати дані обчислення?

( Як доповнити одноцифрове число до одиниці, склад числа 7)

– Чого ми  навчимося сьогодні на уроці?

 

2. Мотивація навчальної діяльності  (з використанням методу «Мікрофон»)

– Навіщо нам потрібно вміти правильно рахувати? Де ви зможете використати ці знання7

 

3.Опрацювання навчального матеріалу

 

•  Математичний диктант (з використанням прийому «Світлофор») Один учень працює біля дошки.

Перший доданок 6, другий – 5, знайти суму …….:( 11)

Збільшити на  4 ……             (15 ):

Зменшити на 6 ……               ( 9 ):

Запиши наступне число …   ( 10 ):

Додай стільки ж                     ( 20):

Запиши попереднє число … ( 19 ):

Знайди різницю отриманого числа і 7   ( 12 ):

На скільки це число більше від 6          ( 6).

Яке число доповнює отримане до 10    ( 4 ).

• Фізкультхвилинка  (з використанням пісеньки « Ми – гриби»)

 

 

• Робота з підручником  ( с.36-37)
  • Вправляння в додаванні і відніманні числа 7 з переходом через десяток  №181,182. (з використанням прийому «Коментування»
  • Закріплення переставної властивості додавання №183. ( самостійна робота з взаємоперевіркою в парах).
  • Складання та розв’язування задач  за графічними моделями № 184.

 

…………………         ………………………        ……………………..

 

( Робота в групах з використанням прийому «Два – чотири – всі разом», усно)

– Чи істинним буде твердження, що ці задачі є взаємооберненими?

• Розв’язування задачі № 185. (під керівництвом вчителя)
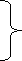  • І група :  складає графічну модель задачі.

                                           ……………

                                                               …………………………….            ?

 

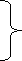• ІІ група : складає репрезентативну модель .

                                           Гр. – 6 кг

                                                                Ябл. - ? , на 7 кг більше            ?

 

• ІІІ група : складає схематичну модель задачі.

 

                                    Розв’язання

1. 6 + 7 =13 (фр.) – яблук:
2. 13 +6 +19 (фр.)

Відповідь: тато купив 19 фруктів.

 

• Побудова прямокутника із зазначеними сторонами, позначення його вершин і знаходження  периметра №186. ( індивідуальна робота із використанням прийому «Тихе опитування»)

 

ІІІ. ЗАКЛЮЧНА ЧАСТИНА

 

1. Домашнє завдання:

Основне – вирази № 187;

Додаткове – скласти і розв’язати задачі за схемами № 188.

 

2. Рефлексія ( з використанням прийому «Світлофор настрою»)

– Чого навчились на уроці?

– Які поняття повторили?

– Що вас найбільше зацікавило?

– Чи досягли успіху, працюючи в групі?.Що цьому сприяло?

– Хто на уроці був найактивнішим?

– Який настрій був у вас на уроці?  ( Учні прикріплюють прищепки із своїми іменами на  «Світлофор настрою»)

– Дякую всім за урок.

 

 

Розгорнутий конспект

 відкритого виховного заходу

з математики

на основі компетентністного підходу до навчання

 

Мета. Узагальнити і систематизувати знання учнів. Формувати математичну компетентність засобами математичного моделювання. Розвивати обчислювальні навички, пам’ять, логічне мислення, творчі здібності учнів. Виховувати бажання співпрацювати в командах, наполегливість у навчанні.

 

 Ведуча 1 Щоб захід наш цікаво розпочати

                 Загадку дам вам відгадати:

                 Наук цариця неосяжна,

                 Могутня, щедра і прекрасна,

                 Блискуче розум розвиває

                 Мислити правильно навчає.

                 Неперевершена її краса!

                 Здогадались, хто така?

                 Звичайно: математика!

Ведуча 2 Сьогодні будемо ми, друзі,

                 Царицю всіх наук вітати.

                 Так можемо гордо і по праву

                  Ми математику назвати.

Ведуча 1 Зустрічайте, цариця Математика з принцесою Логікою та 
принцом Ерудитом!

Математика І сувора, й солов’їна

                    Математики країна.

                       Праця там іде завзята –

                       Вмій лиш спритно рахувати,

                       Вмій ділити й віднімати,

                       Множити і додавати.

                       Вмій кмітливо все збагнути,

                       Першим в відповіді бути.

                       Ледарів у нас немає:

                       Кожен таблиця множення знає.

Логіка     Логіка – теж наука, друже,

                 І потрібна вона дуже.

                 Міркувати вона навчає,

                 Правильно мислити допомагає.

 

Ерудит    Ну а я – принц Ерудит, хоч і не наука,

                 Та потрібна в житті штука.

                 Книг багато я читаю,

                 Всім цікавлюсь, усе знаю.

                 З логікою я дружу,

                 Математику люблю.

                 Точно й швидко я міркую,

                 Та ніколи не нудьгую.

Ведуча 2 Здавна математику називали царицею наук, гімнастикою та музикою для розуму.

Лінь  Міркувати, рахувати, читати…Аж в голові паморочиться! Нащо? ХХІ століття надворі. Інформатику вивчають з 2 класу.

ViWi у кожному під’їзді. Підключився…Набрав три чарівні букви :

ГДЗ. І все. Готово! Ось, хто всіх наук королівна, Лінь – неповторна і чарівна!

Піфагор  Я – Піфагор, батько математики.

                 Я прагнув всіх людей навчити

                 Правильно і швидко лічити.

                 Спробуйте хоча б на мить

                 Неможливе уявить:

                 Мов за помахом руки

                 Зникли числа всі ураз.

                 Як лічити нам зірки?

                 Визначати день і час?

                 Математика для нас

                 Вкрай потрібна повсякчас!

Лінь        А ось хлоп’я, хай нас розсудить:

                 Хто правий, а хто щось блудить.

Хлопчик Хоч сідай та гірко плач –

                 Не люблю отих задач!

                 Через них одні невдачі.

                 Ох, замучили задачі!

                 Всі учіться, хто бажає,

                 Я б здоров’я не втрачав!

                 На умову не зважаю:

                 Раз – помножив, два – додав.

                 Скільки чашок? Скільки ложок?

                 Це ж простеньке завдання.

                 Я додам слона до кішки,

                 Перемножу на коня.

                 Ні, не хитра ця наука!

                 Якщо умову не читать,

                 Може статись…дід за внука

                 Буде меншим літ на п’ять.

                 А друкарські дві машини

                 Косять жито вісім днів.

                 Приїжджають щохвилини

                 Три десятки поїздів.

                 А до Марса…метрів триста.

                  Мудра в мене голова!

                  Півхлоп’яти йде у місто,

                  З ним …півмами. Ну й дива!

Піфагор Як можна так безвідповідально ставитись до математики?

Лінь Відмінно! Геніально! Твоя до віку!

Хлопчик Де я? Хто ви?

Лінь  Це твій тріумф! І ти на святі.

Піфагор Я – Піфагор, залюбки навчу тебе математики. Я склав таблиці додавання та множення. Ти вивчиш їх напам’ять. Будеш уважно читати умову задачі. І твої відповіді будуть правильними.

Лінь  А я дам тобі калькулятор, планшет, смартфон, в якому інтернет. І досить лише цифри знати і вправно дії набирати, і будеш мати результати.

Хлопчик  І вчити нічого не треба?

Лінь Та щоб я забула пароль від ViWi!

Хлопчик Звісно, я іду до тебе.

Піфагор Зачекай. Сьогодні в цій залі відбудеться турнір знавців математики. Гра буде цікава. Залишся ще трохи з нами.

Хлопчик І приз дадуть?!

Піфагор Якщо правильно будеш відповідати.

Хлопчик Гаразд, залишаюся.

Піфагор Тож давайте запросило наших: команду «Кмітливі» та команду «Розумники».

Учениця  Для участі у конкурсі

                  Зібрались наші діти :

                  Кмітливі та розумниці,

                  Знавці та ерудити.

Учень       Їх прийшли підтримати

                  Батьки та однокласники.

                  Палкі уболівальники –

                  Друзі математики.

Учасники Кмітливі, наш девіз:

                  Будемо добре міркувати,

                  додавати й віднімати

                  і свій розум розвивати,

                  щоб найкраще відповідати.

Учасники Розумники, наш девіз:

                   Математику ми любим,

                   З логікою завжди дружим.

                   Наполегливими будем,

                   Перемогу ми здобудем.

Піфагор Спонсор нашого математичного турніру «Піфагорбанк».

За правильну відповідь команда отримуватиме один   піфагор.

 

Математика Усім учасникам успіхів бажаємо,

                       Відповідей правильних від усіх чекаємо

Математичний турнір

Ерудит  На розминку я приготував для вас цікаві ребуси.(по 2 ребуси для команди)

Ерудит  А зараз перевіримо вміння правильно і швидко рахувати.

Ерудит (до хлопчика) Ну, чого ти не радієш?

Хлопчик Тут радій чи не радій:

                Калькулятор не знає порядку дій.

Ерудит Я приготував для вас математичну цікавинку.

(виходять «числа»)

1. Піфагор вважав мене самим важливим, бо від мене починається світ чисел.
2. Давні греки вважали, що 2 – це символ любові, бо двом завжди краще, ніж одному.
3. Число 3 – символічне. Найвідоміший символ трійки – тризуб. А ще кажуть: Бог любить трійцю.
4. Я представлена квадратом, чотири сторони якого означають чотири сторони світу, чотири пори року. Чотири стихії: вогонь,землю, повітря та воду.
5. Мені Піфагор відводив особливе місце, вважаючи божественним: Христос нагодував 5 хлібинами 5 тисяч людей.
6. Мене вважав Піфагор зачарованим числом: в результаті додавання чи віднімання чисел, на які я розкладаюсь, отримують 6. (1 + 2 + 3 = 6   1 х 2 х 3 = 6)
7. А мене називають магічним числом: 7 днів у тижні, 7 кольорів у веселці, 7 нот в музиці, 7 чудес в світі. А ще кажуть: сім разів відміряй, один – відріж.
8. А я втілення надійності,справедливості та безкінечності. Якщо мене розділити навпіл завжди отримують рівні частини. 

      (8 = 4 + 4 4 = 2 + 2  2 = 1 + 1)

9. Надзвичайну силу приписували мені. У древніх греків існувало 9 богів на Олімпі, 9 суддів на Олімпійських іграх. Є також 9 планет в сонячній системі.

Піфагор Зараз ми пропонуємо знавцям розв’язати рівняння:

 

 

Вчитель Вболівальники теж можуть допомогти своїм командам.

       Якщо число ділиться на .., плескаємо,

        не ділиться – присідаємо.

Кмітливі (6): 18, 50, 300,  66, 100, 420.

Розумники (8): 16, 40, 30, 88, 200, 560.

Вчитель У наступному завданні учасники позмагаються у вмінні

складати вирази.          

Вчитель Математика може бути і веселою. Ми пропонуємо вам послухати гумореску «Проста арифметика»

Учениця  Викликає вчитель Люду,

                  Слабшу серед дітвори

                  І питає: «Скільки буде

                  Десять розділить на три?»

                  Розв’язать вона не може,

                  Звісно, знітилась, мовчить.

                  Вчитель каже: «Так не гоже,

                  Бо табличку треба вчить!

                  Хай картоплі є десяток, –

                  Вчитель далі річ веде, –

                  Розділи на трьох дівчаток,

                  То по скільки припаде?»

                   Люда каже: «Зайвий клопіт!

                   І нащо мені це знать?

                   Я зварю картоплі горщик,

                   Потовчу, і хай їдять!»

Вчитель А зараз настав час позмагатися капітанам команд.

                    Конкурс ерудитів

1. Скільки цифр в математиці? (10)
2. Результат дії ділення – (частка)
3. Частина прямої, з одного боку обмежена точкою – (промінь)
4. Яке число зменшили в 50 разів і отримали 20?  (1000)
5. Скільки всього десятків в числі 635? (63)
6. Семеро чекали восьмого 15 хв. Скільки часу чекав кожний? (15 хв)
7. Колоду розрізали на 5 рівних частин. Скільки зробили розрізів? (4)
8. Що легше 1 кг вати чи 100 г заліза? (100 г заліза)
9. У Петрика в руці 2 монети, разом 15к. Одна з них не 5 к. Яка друга монета?
10.  Катруся з дуба рвала груші, у кошик складала: 2 татові, 2 мамі,      2 Катрусі. Скільки всього груш?

1. Коли ми дивимося на цифру 3, а кажемо: 15? (На годиннику)
2. Яка довжина 1/5 м? (2 дм чи 20 см)
3. Замкнена ламана, яка складається з 3 ланок? (Трикутник)
4. Трійка коней пробігла 5 км. Яку відстань здолав кожен кінь? (5 км)
5. Скільки всього сотень в числі 635? (6)
6. Брат старший за сестру на 7 років. На скільки років він буде старший через 10 років? (На 7)
7. На шнурку зав’язали 5 вузликів. На скільки частин розділили шнурок? (На 6)
8. Що важче 10 кг заліза чи 1 ц пір’я? (1ц )
9. На день народження до Білосніжки прийдуть 7 гномів. На скільки рівних частин вона повинна розрізати торт? (На 8)
10.  Кріт виліз з-під землі, а перед ним лежать 5 пшеничних зерняток, 5 житніх і 7 горошин. Скільки всього насінин побачив кріт? (Жодного)

Вчитель  А зараз ми запропонуємо дорослим знову відчути себе дітьми, третьокласниками, пригадати математику.

Логіка  Я приготувала для вас математичну загадку:

• задумайте одноцифрове число
• збільшіть його в 3 рази, додайте2,
• отриману суму помножте на число, зо передує числу 4,
• додайте задумане число,
• закресліть цифру, що вказує на кількість одиниць другого розряду,
• число, що залишилося, збільшіть на 2,
• знайдену суму зменшіть у 4 рази, додайте 8,
• отримане число поділіть на найменше двоцифрове число,
• запишіть отриманий результат.

Це число 1!

Вчитель   А зараз ми пропонуємо командам розв’язати задачу за допомогою рівняння, скласти обернену.

Задача. Для гуртка купили 6 наборів шахів по 35 грн кожний. Яка вартість покупки?

                        Розв’язання

х – вартість покупки;

І спосіб                                  ІІ спосіб

х : 6 = 35                                 х : 35 = 6

х = 35 · 6                                 х = 35 · 6

х = 210                                    х = 210

                          Обернені задачі

х – кількість наборів;           х –  ціна набору;

35 · х = 210                            х · 6 = 210

х = 210 : 35                            х = 210 : 6

х = 6                                        х = 35         

Піфагор  Ну, чого ти, хлопче, скис?

Хлопчик У мене інтернет завис…

Піфагор  Що, зрозумів, що математику треба вчити?

Хлопчик  Треба спочатку переконатися, чи потрібна вона в житті. Піду дорослих запитаю.  Де ви використовуєте знання з математики?

( відповідають батьки)

Хлопчик (до вболівальників) А ви вчитеся?

( Вболівальники розказують прислів’я про навчання)

Вчитель Настав час підвести підсумки нашого турніру. Оскільки на сьогоднішній день монети-піфагори не використовують, то я пропоную вам обміняти їх на 12 балів з математики.

Математика Всі добре працювали,

                       Старались, як могли.

                       Логічно міркували,

                       Так швидко рахували,

                       Правильно відповідали. 

                       Мене не підвели!

Хлопчик       Не махну на все рукою,

                       Лінь прогоню: відчепись!

                       Бо чого навчуся в школі,

                       Знадобиться ще колись.

                        Я ж бо прагну досягнути

                        У житті своїм вершин.

                        Математику збагнути

                        Мушу точно, до глибин.

Піфагор         Так, математика – наука,

                        Вона не кожному дана.

                        Але як добре постаратись,

                        Повчити, трохи позайматись,

                        То враз побачиш ненароком,

                        Що та наука – не морока.

Лінь  Можна і я буду вчитись?

Всі  Можна!

Ведуча 2         Така вона – наук усіх цариця,

                         Шляхетна,мудра, добра і весела.

                         Її корона сонячно іскриться

                         У кожній школі, у містах і селах.

Ведуча 1          О, математико,

                         Без тебе не ступиш ні кроку,

                         Без тебе, як на суші без води.

                         Твої неповторні уроки

                         В серцях наших будуть завжди.

                         Манить нас знань велична висота.

                         Така  солодка нам навчання мука.

                         Ми любим всі науки, та…

                         Найкраща – математика наука!

 

Учні виконують пісню «Будемо рахувати»  (муз. і сл. А. Олейнікової)

 

                       Математика – наука

                       Дуже складна, як для нас.

                       Віднімаєм і складаєм,

                       І рахуємо весь час.

                            Приспів

                       Час не будем гаяти

                       Мусимо все знати:

                       Додавать і віднімать,

                       Будем рахувати.

 

                       Моя киця народила

                       Дуже милих кошенят.

                       Двоє чорних, двоє білих.

                       Скільки всього оченят?

 

                       Тато дав мені цукерки,

                       Щоби друзів пригостить.

                       Та не можу п’ять цукерок

                       На трьох друзів розділить.

 

 

                       Математику вивчаєм,

                       щоб уміти рахувать.

                       А коли її пізнаєм

                       Можем вченими вже стать.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Інтегровані задачі

для 1 класу

 

 

 

1. Довжина синього кита 33 м, а річкового сома – 3 м. На скільки метрів кит довший від сома?

 

2. Маса бичка 25 кг , а поросятка – 10 кг. На скільки кілограмів бичок важчий від поросятка?

 

3. Олежик купив у шкільній їдальні піцу за 5 грн і булочку з повидлом за

3 грн і заплатив 10 грн. Скільки здачі отримає хлопчик?

 

4. У класі навчаються 12 дівчаток і 17 хлопчиків. Скільки учнів у класі?

 

5. У класі 29 учнів, з них 12 дівчаток. Скільки хлопчиків у класі?

 

6. За день магазин продав 35 кг бананів і залишилось ще 23 кг. Скільки кілограмів бананів було в магазині спочатку?

 

7. Маринка використала 7 аркушів кольорового паперу і в неї залишилось ще 11 аркушів. Скільки аркушів кольорового паперу в упаковці?

 

8. Мама спекла тістечка. 6 тістечок вона дала дітям, а 12 склала на тарілку. Скільки тістечок спекла мама7

 

9. Коли з автобуса вийшло 5 пасажирів, у ньому залишилось 12. Скільки пасажирів було в автобусі спочатку?

 

10. В автобусі їхало 16 пасажирів. Після того, як на зупинці декілька пасажирів вийшло, залишилось 12. Скільки пасажирів вийшло з автобуса?

 

11. Тато купив 25 кг цукру. Коли мама зварила варення, залишилось 20 кг цукру. Скільки кілограмів цукру використала мама?

 

12. У Павлика було 100 грн. Він купив конструктор за 60 грн. Скільки здачі отримає хлопчик? Які це можуть бути купюри?

 

13. Лялька коштує 70 грн. а ведмедик – на 25 грн дорожчий. Скільки коштує ведмедик?

 

14. Конструктор коштує 80 грн. а м’яч – на 30 грн дешевший. Скільки коштує м’яч?

 

15. На майданчику гралось 12 дітей. До них прийшло ще 5. Скільки дітей стало на майданчику?

 

16. У гуртку займалось 14 першокласників і 12 другокласників. Скільки учнів займались у гуртку?

 

17. Золотомушка – найменша пташка в Україні, її зріст становить пів дециметра. Скільки це сантиметрів?

 

18. Бурий ведмідь – найбільший звір в Україні. Гудіння бджіл він чує на відстані 5 км, а запах меду – на 3 км дальше. На якій відстані ведмідь відчуває запах меду?

 

19. Дід Роман зловив сома. завдовжки 2 м. Довжина найдовшого сома, впійманого в Україні 9 м. На скільки коротший сом?

 

20. Мама дала Маринці на шкільний обід 15 грн. Які це могли бути купюри?

 

21. Сергійко лягає спати о 21.00, а прокидається о 7.00. Скільки часу спить хлопчик?

 

22. Любочка виходить з дому до школи о 7 год 50 хв і йде 10 хв. О котрій годині вона приходить до школи?

 

23. Данилко щоранку приходить до школи о 8 год, на дорогу до школи хлопчик витрачає 20 хв. О котрій годині він виходить з дому?

 

24. Тетянка запросила в гості 3 подружок. Скільки тістечок до чаю треба купити дівчинці, щоб їх пригостити?

 

25. Квиток в театр коштує 25 грн. Якими двома купюрами треба заплатити за квиток, щоб отримати 5 грн здачі?

 

26. Довжина басейну 25 м. Яку відстань проплив Павлик, пропливши 2 басейни?

 

27. 12 хлопчиків вирішили зіграти в футбол. Як їм розділитись на команди?

 

28. У Івасиковому лего 40 деталей, а в Петриковому – на 15 більше. Скільки деталей в лего Петрика7

 

29. Софійка пройшла від дерева до куща 8 кроків, а Юрко – 7. Чиї кроки довші?

 

30. Христина з Аліною катались на велосипедах 30 хв. Скільки часу каталась кожна дівчинка?

 

 

 

.