Реальні гази. Рівняння Ван-дер-Ваальса
Тема уроку. Реальні гази. Рівняння Ван-дер-Ваальса
Мета уроку:
- встановити суттєві відмінності між ідеальним й реальним газами;
- ознайомити учнів з поправками Ван-дер-Ваальса до рівняння стану ідеального газу, які роблять можливим його застосування для реального;
- навчитися застосовувати даний матеріал до розв’язування фізичних задач;
- розвивати логічне мислення учнів.
Обладнання. Інтерактивна дошка, роздатковий матеріал (таблиця властивостей ідеального та реального газів, таблиця поправок Ван-дер-Ваальса для реальних газів, роздатковий матеріал, відеоролики, презентація).
Хід уроку
І. Вступне слово вчителя. Сьогодні в нас незвичний урок. Ми помандруємо у світ науки фізики, щоб на основі вивченого матеріалу, відкрити для себе щось нове. А для цього нам потрібно пригадати, що ж ми вивчали на попередніх уроках.
(Відповіді учнів)
ІІ. Рефлексія
Учитель. У якому світі ми щойно з вами мандрували? (У Мікросвіті)
А якими світами ми ще з вами мандрували, вивчаючи фізику? (Мега- й Макро- світи)
Так, ми подорожували з вами різними світами (учні разом з учителем згадують вивчені фізичні закони й поняття, намагаються прокласти місточок між світами). Ця мандрівка допомогла нам зрозуміти найголовніше: ці світи невід’ємні один від одного, адже основою Мега- й Макро світів є Мікросвіт, не знаючи будови та законів розвитку якого ми не можемо зрозуміти й пояснити закономірності їх розвитку.
У цьому напрямку працювало багато вчених, серед яких А. Ейнштейн, І. Ньютон, М. Ломоносов, Р. Броун, Я. Френкель, Д. Менделєєв, А. Іоффе, Р. Міллікен та багато інших. Їх пояснення, дослідження та відкриття на сьогодні широко використовуються в побуті, техніці й науці.
Під час розповіді учителя на інтерактивній дошці йде відеоролик №1
(Слайд 1)
ІІІ. Актуалізація опорних знань
Учитель. Пропоную згадати матеріал, який ми вивчили на попередніх уроках.
Завдання 1. «Продовж думку» (слайд 2 ).

Учні повинні продовжити речення, що з’являється на інтерактивній дошці.
Завдання 2. «Від мови формул до звичайної мови» (cлайд 3).
Пропоную учням перевести мову фізичних формул на звичайну мову, тобто назвати фізичні величини й закони, зображені за допомогою математичної моделі.

Завдання 3. «Прокоментуй побачене».
Пропоную віртуальний дослід без звуку. Учні, проглянувши відеоролик, повинні прокоментувати побачене.
Відеоролик №2 Залежність тиску газу від об’єму при сталій температурі (cлайд 4).

Відеоролик №3 Залежність тиску газу від температури при сталому об’ємі (Слайд 5).

ІІІ. Мотивація навчальної діяльності
Переглянувши відео сюжети і повторивши матеріал із розділу «Основи МКТ», формулюю гіпотезу: «Усе щойно повторене можна застосувати для реальних газів.»
Вправа. «Обґрунтуй свою думку»
Пропоную учням дати відповідь на запитання, обгрунтувавши її: чи згодні вони зі мною (cлайд 6).

Після виступів учнів оголошую тему уроку, вивчення якої допоможе прийти до правильного вирішення даної проблеми (cлайд 7)/

Разом з учнями з’ясовуємо завдання уроку (cлайд 8).

ІV. Сприйняття й засвоєння нового матеріалу.
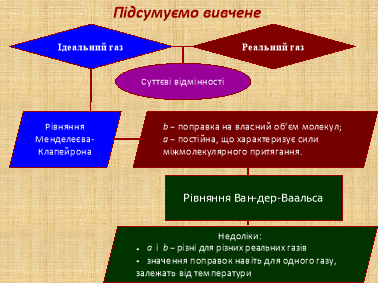
Завдання 1. Встановити різницю між властивостями ідеального й реального газу (слайд 9)/

Учитель. Ми з вами знаємо, що модель ідеального газу безвідмовно працює або при високих температурах, коли хаотичний тепловий рух настільки інтенсивний, що молекули рухаються, не звертаючи увагу одна на одну, або при малій густині, коли між молекулами дуже велика відстань і вони не можуть «відчувати» одна одну. Під час охолодження й стискання, коли вплив молекулярної взаємодії стає більш помітним, газ може перетворитися в рідину.
Отже, для переходу газу в рідину потрібно враховувати молекулярні взаємодії. Модель ідеального газу при даних умовах не працює. А працює модель реального газу. Що ж таке реальний газ?
Реальний газ – газ, властивості якого істотно залежать від взаємодії молекул. У звичайних умовах, коли середня потенційна енергія взаємодії молекул багато менша їх середньої кінетичної енергії, властивості реального газу не суттєво відрізняються від властивостей ідеального газу й до нього можна застосовувати закони, встановлені для ідеального. Але при низьких температурах і дуже малому об’ємі, тобто при охолодженні та стисканні, реальний газ не підлягає рівнянню стану ідеального газу Менделєєва-Клапейрона. Це пояснюється тим, що молекули мають власний об’єм і між ними існують сили міжмолекулярної взаємодії.
Одним із перших, хто запропонував рівняння стану реального газу, був голландський фізик Ван-дер-Ваальс. У 1873 р. він ввів до рівняння Менделєєва-Клапейрона поправки на розмір молекули й на силу взаємодії між ними.
Голландський фізик запропонував модель реального газу, у якої молекули вважаються твердими кульками діаметром d і займають хоч малий, але деякий об'єм. При цьому вони не лише відштовхуються при зіткненнях, але ще й притягуються одна до одної слабкими силами на відстанях, порівняних з розмірами молекули.
У 1910 році за свої дослідження він отримав Нобелівську премію (слайд 10).

Пропоную учням проаналізувати й знайти відмінність у рівнянні стану ідеального газу (рівнянні Менделеєва-Клапейрона) та рівнянні стану реального газу (рівнянні Ван-дер-Ваальса) (слайд 11).
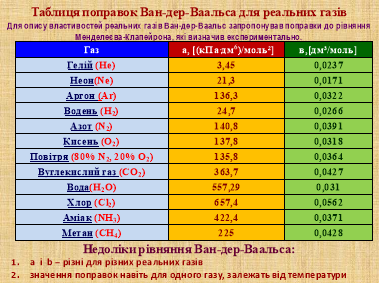
При визначенні відмінностей пояснюю їх. Знайомлю учнів із поправками Ван-дер-Ваальса: поправкою на власний об’єм молекули (b) та поправкою, що характеризує сили міжмолекулярної взаємодії (a) (таблиця, слайд 12).
Учитель. Рівняння Ван-дер-Ваальса не досконале. Воно має певні недоліки:
- різні реальні гази мають свої поправки Ван-дер-Ваальса;
- значення поправок навіть для одного реального газу залежить від температури;
- рівняння Ван-дер-Ваальса розходиться з експериментом для двофазних станів.
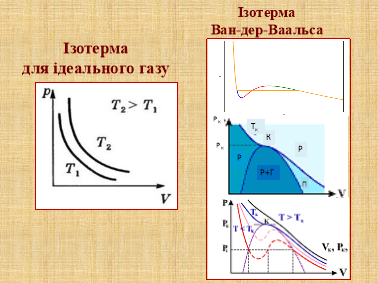
Для порівняння пропоную учням розглянути графіки ізотерми для ідеального газу та ізотерми Ван-дер-Ваальса (слайд 13).
V. Закріплення нового матеріалу
Кожен учень отримує картку із завданнями. І варіанту пропоную розв’язати завдання, вважаючи газ ідеальним, ІІ варіанту – вважаючи газ реальним.
Завдання 1.
Моль азоту охолоджений до температури -100°С. Визначити тиск, спричинений газом на стінки посудини, об'ємом V=1,00 л
(І варіант – рід.=1,44·106Па; ІІ варіант – рреал.=1,36·106Па).
Завдання 2.
Порівняти тиск, що спричиняє азот, будучи реальним газом із тиском, який спричиняв би цей газ, якби зберіг за даних умов властивості ідеального газу
(рреал.=0,95рід.).
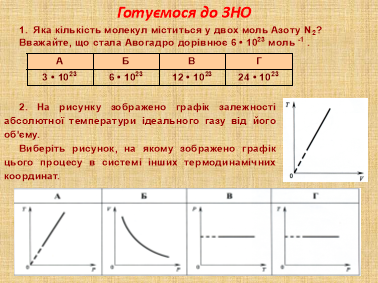
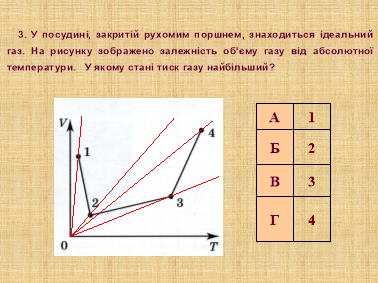
Завдання 3. «Готуємося до ЗНО»
Ті знання, які ви одержали на попередніх уроках і сьогодні, можуть бути використані на ЗНО.
Я пропоную вам за 5 хвилин розв’язати наступні завдання (слайди 14, 15)
VI. Підсумок уроку. (Слайд 16).
VII. Домашнє завдання (слайд 17).
- Вивчити конспект;
- Розв’язати завдання № 2.
Моль азоту розширюється адіабатно в порожнечу, внаслідок чого його об'єм збільшується від V1=l,00 л до V2=10,0 л. Визначити приріст температури газу ∆Т, якщо а) азот – ідеальний газ; б) азот – реальний газ. Отримані результати порівняти.
- Повторити §1-14 «Фізика-10» (Є.В. Коршак, О.Ш. Ляшенко, В.Ф. Савченко) або §1-11 «Фізика-10» (С.У. Гончаренко).
Савельев > Частина 2. Молекулярна фізика і термодинаміка > 2.7. Рівняння Ван-дер-Ваальса
Задача № 2.162
Моль азоту охолоджений до температури -100 °С. Визначити тиск p, що спричиняє газ на стінки судини, якщо об'єм V, займаний газом, рівний: а) 1,00 л, би) 0,100 л. Порівняти тиск, спричинений азотом на стінки, як реальним газом із тиском , якби він зберіг за даних умов властивості ідеального газу.
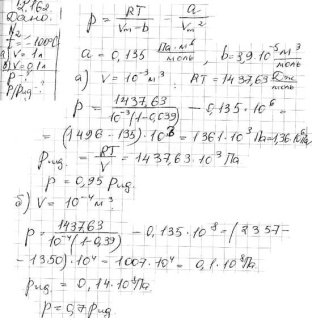
Задача № 2.165
Моль азоту розширюється адіабатно в порожнечу, внаслідок чого об'єм газу збільшується від V1=1,00 л до V2=10,0 л. Визначити ∆T приріст температури газу.

Задача № 2.166
Два моля водню розширюються в порожнечу, внаслідок чого об'єм газу збільшується від значення V1=2,00 л до V2=10,0 л. Яку кількість теплоти Q потрібно повідомити газу, аби температура його не змінилася?

Задача № 2.168
Моль кисню, що займав спочатку об'єм V1= 1,000 л при температурі -100 °С, розширився ізотермічно до об'єму V2=10,00 л. Знайти:
а) приріст внутрішньої енергії газу ∆Um,
б) роботу А, реальним газом (порівняти А з роботою A, обчисленою за формулою для ідеального газу).
в) кількість теплоти Q, отримана газом.

2.176.
Знайти вираження для ентропії моля ван-дер-ваальсовского газу (залежно від T і V). Порівняти отримане вираження з аналогічною формулою для ідеального газу.
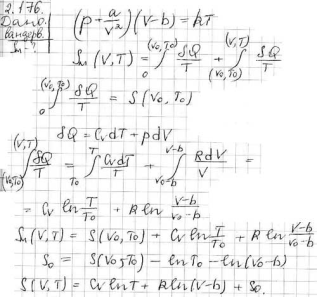
1

про публікацію авторської розробки
Додати розробку
