Різнорівневі завдання по темі "Тотожність. Тотожні вирази"

Різнорівневі домашні завдання або для самостійної роботи

«Тотожність. Тотожні вирази»

І рівень

Завдання 1

Чи є тотожно рівними вирази:

1.     8(a – b + c) i 8a – 8b + 8c;
2.     -2(x – 4) i -2x – 8;
3.     (5a – 4) – (2a – 7) i 3a – 11?

Завдання 2

Які вирази тотожно рівні:

1.     3(x + y) i 3x + 3y;
2.     4,8(a + b) i 4,8a + b;
3.     4(m – 3) i 4m – 3;
4.     5,7(x + y) i 5,7x + 5,7y;
5.     (a – b)·8 + a i 7a – 8b;
6.     1 – a + b i 1 – (a – b)?

Завдання 3

Серед виразів -10a + 7, -10a – 7, -14a + 7, -14a – 7 знайдіть такий, який тотожно дорівнює виразу -12a + (7 – 2a).

Завдання 4

Довжина однієї із сторін трикутника а см, а довжина кожної з двох інших сторін на 2 см більша. Запишіть у вигляді виразу периметр трикутника та спростіть цей вираз.

ІІ рівень

Завдання 1

Запишіть у вигляді тотожності:

а) добуток довільного числа і нуля дорівнює нулю;

б) добуток двох чисел дорівнює добутку протилежних їм чисел;

в) квадрат числа дорівнює квадрату протилежного йому числа.

Завдання 2

Заповніть таблицю:

Чи тотожні вирази |x| + 3 і х + 3? Обґрунтуйте відповідь.

Завдання 3

Які з наведених рівностей є тотожностями:

1.    
2.    
3.    
4.    
5.    
6.    
7.    
8.     ?

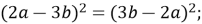
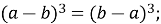
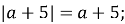
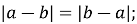
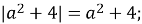
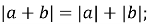
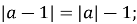
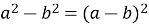ІІІ рівень

Завдання 1

Доведіть, що за будь яких a i b значення виразу

дорівнює 2.

Завдання 2

Складіть вирази для обчислення площі фігури, зображеної на рисунку, спочатку доповнивши фігуру до прямокутника, а потім розбивши її на два прямокутники. Доведіть тотожність утворених виразів. (Рис. 1.)

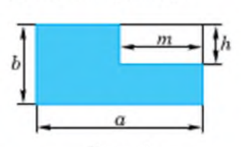
Рис. 1