Робота МАН "Ознаки подільності і їх застосування"

    Міністерство освіти і науки, молоді та спорту України

    Департамент освіти і науки Полтавської облдержадміністрації

    Полтавське територіальне відділення МАН України

    Кобеляцьке районне наукове товариство учнів «Мала академія наук»

                                                                Відділення : математики

                                                                Секція :математика

                                                               Підсекція: математика

                  Ознаки подільності та їх застосування

                                                           Роботу    виконала:

                                                           Овчаренко Дарія Юріївна

                                                                             учениця  8 класу

                                                                             Григоро - Бригадирівської

                                                                             загальноосвітньої школи І- ІІ ступенів

                                                                             Кобеляцької  районної ради

                                                                             Науковий керівник  :  

                                                                             Мирошниченко Алла Миколаївна ,

                                                                             учитель математики і фізики

                                                                             Григоро - Бригадирівської                                                                             

                                                                             загальноосвітньої школи І-ІІ ступенів

                                                                             Кобеляцької районної ради,    

                                                                             спеціаліст вищої категорії                                                         

 

 

                                              Кобеляки - 2018                                                  

                                       Тези

 науково-дослідницької роботи «Ознаки  подільності та їх застосування»

Автор: Овчаренко Дарія Юріївна, учениця  8 класу Григоро-Бригадирівської  ЗОШ І-ІІ ступенів Кобеляцької ради Полтавської області

Науковий керівник:  Мирошниченко Алла Миколаївна, учитель математики    і   фізики Григоро-Бригадирівської  загальноосвітньої школи І-ІІ ст., Кобеляцької районної ради,  Полтавської області спеціаліст вищої   категорії  .  

Мета роботи: знайти і систематизувати ознаки подільності, що дозволяють вирішити завдання, не вдаючись до громіздких рішень і висновків.

Об'єкт  дослідження - вивчення всіляких ознак подільності.

Предмет дослідження -  вивчення  ознак подільності та  застосування  їх у загальноосвітній школі.

 Для досягнення цієї мети необхідно вирішити наступні завдання:

1) Самостійно дослідити подільність чисел.

2) Вивчити додаткову літературу з метою ознайомлення з іншими ознаками подільності.

3) Об'єднати та узагальнити ознаки з різних джерел.

 4) Зробити висновок.

Актуальність роботи: в школі вивчаються лише ознаки на 2, 3,  5,  9 та 10, а для того щоб успішно брати участь в інтелектуальних конкурсах, «Кенгуру», «Шкільні дні» та олімпіадах з  математики, обов’язково потрібно знати й інші ознаки подільності.

 

 

                                                       ЗМІСТ

Вступ…………………………………………………………………………….4-6

 Розділ 1. Подих історії………………………………………………………..  7-9

1.1.З історії розвитку подільності…………………………………………….. 7-8

1.2. Дії над натуральними числами в стародавні часи…………………………9

 Розділ 2. Ознаки подільності…………………………………………….     10-17

2.1. Подільність за останніми  цифрами числа……………………………..10-11

2.2. Рекурентний  метод…………………………………………………………12

2.3. Встановлення ознак подільності шляхом розбивання числа на одно, двох і трьохзначні грані справа наліво……………………………………………   13-15

2.4. Ознаки подільності чисел  виду 10n + 1, 10n – 1………………………16-17

2.5. Таблиця подільності………………………………………………………   17

Розділ 3. Застосування ознак подільності………………………………….  18-21

3.1. Приклади  розв’язування задач на використання ознак   подільності..18-20                      

3.2. Задачі на застосування ознак подільності……………………………….    21

Висновок………………………………………………………………………22-23

Список використаних  джерел………………………………………………….24

Додатки…………………………………………………………………........25-  30

Відгук керівника………………………………………………………………… 31

Електронний варіант роботи на диску СД-R

Презентація

 

 

                                               ВСТУП

 

«Якщо ви хочете навчитися плавати, то сміливо входите у воду, а якщо хочете навчитися вирішувати завдання, то вирішуйте їх».( Д. Пойа )                                                                  У арифметиці багато розділів і один з них - подільність чисел. При вивченні на уроках математики теми «Ознаки подільності чисел на 2, 3, 5, 9,10» виник інтерес до дослідження чисел на подільність. Було припущено, що якщо можна визначити подільність чисел на ці числа, то повинні бути ознаки, за якими можна визначити подільність натуральних чисел на інші числа.

     Ознака подільності - це правило, за яким, не виконуючи ділення, можна встановити, чи ділиться одне число на інше. Ознаки подільності завжди цікавили вчених різних часів і народів. Старовинна східна притча: «Давним-давно жив-був старий, який, вмираючи, залишив своїм трьом синам 19 верблюдів. Він заповідав старшому синові половину, середньому - четверту частину, а молодшому - п'яту. Не зумівши знайти рішення самостійно (адже завдання в «цілих верблюдах» рішення не має), брати звернулися до мудреця. - О, мудрець! - Сказав старший брат. - Батько залишив нам 19 верблюдів і велів розділити між собою: старшому - половину, середньому - чверть, молодшому - п'яту частину. Але 19 не ділиться ні на 2, ні на 4, ні на 5. Чи можеш ти, о, високоповажний, допомогти нашому горю, бо ми хочемо виконати волю батька? - Немає нічого простіше, - відповів їм мудрець. - Візьміть мого верблюда і йдіть додому. Брати  легко розділили 20 верблюдів навпіл, на 4 і на 5. Старшій брат отримав 10, середній - 5, а молодший - 4 верблюда. При цьому один верблюд залишився (10 +5 +4 = 19). Засмучені, брати повернулися до мудреця і поскаржилися: - О, мудрець, знову ми не виконали волю батька! Ось цей верблюд - зайвий. - Це не зайвий, - сказав мудрець, - це мій верблюд. Поверніть його і йдіть додому».                                                                     

Методи дослідження: аналіз, синтез, порівняння. Робота має практичне застосування. Її можуть використовувати школярі і дорослі при вирішенні реальних ситуацій; вчителі, як при проведенні уроків з математики, так і на факультативних курсах та додаткових заняттях на повторення. Дане дослідження буде корисним для учнів при самостійній підготовці до випускних і вступних іспитів. А також буде корисно і для учнів, метою яких стали високі місця на міських олімпіадах.

Останні десятиріччя можна з упевненістю назвати революційними, періодом бурхливого розвитку новітніх комп’ютерних технологій, через що елементарні теорії математики, начебто, відійшли на другий план, стали не такими «популярними» серед науковців. Разом із тим, сьогодні природничі науки потребують високого рівня застосування математики. Саме тому у роботі я хочу звернути увагу на актуальність використання нині класичних підходів до подільності в математиці, її доступність та практичну значимість у застосуванні.

Певно, зараз люди частіше користуються калькуляторами, аніж рахують усно. Але багато століть тому наші попередники навчилися підраховувати остачу, частку та виконувати багато інших обчислень без використання електронних технологій. Це забезпечувало проведення обчислювальних робіт у різних галузях науки.Фактично, саме тому вчені створили саму науку математику, не маючи ні комп’ютерів, ні інших обчислювальних пристроїв. Вони хотіли самі осягнути та зрозуміти закони природи і суспільства за допомогою математики та передати ці знання своїм наступникам. Дотепер ми користуємося ними. Як казав Ейнштейн, «хоч би як добре працювала машина, вона зможе розв'язувати всі задачі, що ставляться перед нею, але сама жодної задачі не придумає» - хоч зараз є різноманітні пристрої для полегшення роботи людини з цифрами, «нову арифметику» ще ніхто не придумав. Я у своїй роботі працювала  із  подільністю чисел, намагаючись повторити вивчене раніше, пізнати для себе щось нове, цікаве, дослідити та вивести нові ознаки.

 «  Цифри не правлять світом, але вони  показують, як управляється світ» . Й.В.Гете.

“ Ми наближаємось до того утопічного часу, коли на долю математики залишиться тільки складання рівнянь; розв’язувати ці рівняння будуть машини”. Так сказав академік С.І.Вавілов.

Сьогодні важко уявити собі, як розвивалася б наука, техніка, виробництво, якби не було сучасних  комп’ютерів, планшетів, мікрокалькуляторів. Саме завдяки бурхливому розвитку обчислювальної техніки і електроніки було досягнуто дивовижних успіхів у створенні і запуску штучних супутників Землі, космічних ракет, кораблів, станцій. За допомогою електроніки роблять складні операції, які рятують життя людині. ЕОМ  керує машинами, грає в шахи, різні ігри, допомогає проводити фізичні та хімічні досліди.

Звичайно виникає запитання:  чи потрібно зараз  вміти рахувати усно, знати табличку множення?  Я переконана: потрібно.  Для загального розвитку, для практичних розрахунків під час відвідування  торгівельних, розважальних центрів (чи станемо ми перевіряти розрахунки в цих місцях за допомогою калькулятора?). У випускних класах ( 4,9,11 ) учні складають державну підсумкову атестацію, випускники  здають зовнішнє незалежне оцінювання  з математики,  де не дозволяють користуватися калькуляторами, телефонами, планшетами. А різноманітні математичні конкурси  “Кенгуру ”, “ Олімпус “,  “Золотий ключик ”, математичні олімпіади різних  рівнів,  змагання…

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 1

ПОДИХ ІСТОРІЇ

 

 

1.1. З історії розвитку подільності

Протягом більше 25 століть задачі теорії чисел були улюбленою областю дослідження визначних математиків і багатьох тисяч дилетантів. В теорії чисел значне місце відводиться теорії подільності цілих чисел, зокрема цілих додатних натуральних чисел, висновки і результати вивчення якої поширюються і на цілі від'ємні числа.

Ще в Стародавній Греції, в так званій піфагорійській школі (6 ст. до н.е.), вивчалась подільність цілих чисел. Були відокремлені окремі підкласи цілих чисел, як наприклад, прості числа, складені, квадратні і тому подібні; вивчалася структура так званих досконалих  і дружніх чисел. 

    Евклід у своїх «Началах» чи «Елементах» дав систематичну побудову теорії подільності. Він вперше запропонував теорему про однозначність розкладу натурального числа на прості множники, яка відіграє основну роль у теорії подільності цілих чисел, і з її допомогою побудував арифметику раціональних чисел. Евкліду були відомі чотири досконалі числа: 6,28,496,8128. Він довів теорему, що N= є досконалим, якщо є простим.

Математики приділяють багато уваги простим числам. Були спроби дізнатися по зовнішньому вигляду просте чи складене це число, а далі вже розглядалась і їх подільність.

  Великий внесок у вивчення ознак подільності чисел вніс Б. Паскаль.

Блез Паскаль (Blaise Pascal) (1623-1662), французький релігійний мислитель, математик і фізик, один з найвидатніших умів 17 століття. Народився в Клермон-Феррані (провінція Овернь) 19 червня 1623. Юний  Блез  дуже рано виявив видатні математичні здібності, навчившись вважати раніше, ніж читати Свій перший математичний трактат «Досвід теорії конічних перетинів» він написав у 24 роки. Приблизно в цей же час він сконструював механічну підсумовує машину, прообраз арифмометра. Роботи Паскаля в галузі точних наук, чи ранній період його творчості відноситься до 1640-1650 році. За ці 10 років різнобічний учений зробив дуже багато: він знайшов алгоритм для перебування ознак подільності будь-якого цілого числа на будь-яке інше ціле число, сформулював спосіб обчислення біноміальної коефіцієнтів, виклав ряд основних положень елементарної теорії ймовірності, вперше точно визначив і застосував для доказу метод математичної індукції . Разом з Галілеєм і Стевіном  Паскаль розробив основні положення класичної гідростатики і встановив її основний закон - «Закон Паскаля». Помер Паскаль в Парижі в 1662 році. Ознака подільності Паскаля. Натуральне число а розділиться на інше натуральне число b тільки в тому випадку, якщо сума добутків цифр числа а на відповідні залишки, одержані під час ділення розрядних одиниць на число b, ділиться на це число. Наприклад: число 2814 ділиться на 7, так як ділиться на 7. (Тут 6-залишок відділення 1000 на 7, 2 - залишок від ділення 100 на 7 і 3 - залишок від ділення 10 на 7).

 

 

 

 

 

 

 

 

1.2. Дії над натуральними числами  в стародавні часи

Ділення натуральних чисел деякі вчені стародавнього світу вміли виконувати ще  кілька тисячоліть тому. Ця математична дія тоді вважалася найважчою,бо люди не знали сучасних правил ділення, та й числа записували не так, як записують тепер. Спробуйте, наприклад,  поділити число  Т на К або CL IV  на  X I V. Колись ділили одне число на інше, використовуючи камінці або кісточки слив.  В середні віки, у період занепаду наук, вона вважалася такою складною, що людям, які вміли виконувати добре ділення,присуджували вчені ступені. В  VII ст. ірландського ченця  Берда, прозваного  Високоповажним, вважали найосвіченішою людиною тому,що він умів майстерно виконувати ділення. Йому приписують слова: « Хто вміє ділити, тому жодна справа не здаватиметься важкою». Таку саму думку висловлює в XVI ст. французький математик П’єр  Рамсу «Потрібен хороший розум, хороша пам'ять і хороша рука для щоденного вправляння  в діленні тому, що велика різноманітність обчислень потребує високого розуму  постійної уваги і вірної руки більше, ніж будь-де . І ніхто не може вважати, що він воістину старанно займається математикою, якщо кожного дня під час занять арифметикою не робить ділення над кількома по можливості більшими числами».                                                                                               Чи можна,не виконуючи ділення, а тільки за зовнішнім виглядом числа встановити, чи ділиться, наприклад, число 19348 на 2, число 917595 на 5, 38745 на 3. Щоб, не виконуючи ділення, встановити, ділиться, чи не ділиться  одне число на інше, користуються ознаками подільності.

 

 

 

 

 

 

                                                        РОЗДІЛ 2

                                      ОЗНАКИ ПОДІЛЬНОСТІ

 

 

2.1. Подільність за останніми цифрами числа

Відмітимо загальновідомі зі шкільного курсу математики ознаки подільності на 2, 5, 10, 4, 8, 25.

2.1.1. Ознака подільності на 2

Теорема 2.1. На 2 ділиться без остачі будь-яке ціле число,  перший розряд якого парний (0, 2, 4, 6, 8). N2, де N=10a+b (a Z, b Z), якщо b2, тобто b=0, 2, 4, 6, 8.

Доведення: Нехай . Будь-яке ціле число можна представити у вигляді суми першого розряду та решти чисел. Тоді N=10a+b (b – перший розряд, а – число, що складається з решти розрядів). 10a2 (за властивістю 3, додаток А). Таким чином на 2 має ділитися b. Оскільки воно лежить в межах від 0 до 9, і є натуральним числом, то воно може бути одним з п’яти наступних чисел: 0, 2, 4, 6, 8.

2.1.2. Ознака подільності на 5 і 10

Теорема 2.2.N5, де N=10a+b (a Z, b Z), якщо b5, тобто b=0 або 5.

Теорема 2.3.N10, де N=10a+b (a Z, b Z), якщо b= 0.

Отже, на 5 ділиться будь-яке ціле число, перший розряд якого 5 або 0, а на 10, якщо у розряді одиниць стоїть 0.

2.1.3. Ознака подільності на 4 і 25

Теорема 2.4. Число ділиться на 4 тоді, якщо число, утворене його двома останніми                                                                                                  цифрами ділиться на 4. N4, де , якщо(10а₁ + а₀)4.

Доведення: Нехай = 100 + 10а₁ + а₀ = 100а + b

100а4, тому число N4, якщо b = (10а₁ + а₀)4.

 

 

Теорема 2.5.N25, де , якщо (10а₁ + а₀)25.

 

 2.1.4. Ознака подільності на 8

Теорема 2.6. Число ділиться на 8 тоді і тільки тоді, якщо число, утворене його трьома останніми цифрами ділиться на 8. N8, де , якщо (100а₂ +10а₁ + а₀)8.

Доведення: Нехай = 1000 + 100а₂ + 10а₁ + а₀ = 1000а + b, де a Z,  b Z і b = 100а₂ + 10а₁ + а₀

1000a8, тому число N8, тоді і тільки тоді, коли b8. Але b і є числом, утвореним трьома останніми цифрами числа N.

Приклад 2.1.6.1. Число 521288, бо 1288 = 16

 Наведемо інші інтерпретації ознаки подільності на 8.

Теорема 2.7. Якщо число сотень є парне, то число утворене двома останніми цифрами повинне ділитися на 8.             
Якщо ж число сотень є непарним, то до числа, утвореного двома останніми цифрами, потрібно додати 4. Таке число повинне ділитися на 8.

Приклад 2.1.7.1.

 а) 6248, бо 6 – парне і 248.

 б) 3528, бо 52+4=56 і 568.

Перечисленні ознаки подільності є простими, зручними у використанні. Але подільність за останніми цифрами може бути використана для обмеженої кількості дільників.

 

 

 

 

 

 

 2.2. Рекурентний метод

 Рекурентний алгоритм ділення числа N на число n полягає в утворенні деякої послідовності чисел N₁, N₂ … N_n, де

 N₁ = N-n (N₁ n),

 

N₂ = N₁-n (N₂ n),

 …………………

 N_n = N_n-1-n (N_nn)

 Якщо N_n = 0, то Nn, якщо N_n 0, то N не ділиться націло на n.

Його суть – у поступовому віднімання від числа N числа n. Якщо різниця на якомусь етапі співпаде з числом n, то Nn.

 При високих значеннях N і порівняно невеликому n цей процес довготривалий, тому сам спосіб, незважаючи на простоту, є неефективним.

 Якщо модифікувати цей алгоритм, утворивши послідовність N₁, N₂ … N_n, де

 N₁ = N - 10^k∙n∙r, (, N₁ ≤ 10^k∙n∙rі N>10^k∙n∙r),

 N₂ = N₁ -10^k-1∙n∙m, (N₂ ≤ 10^k-1∙n∙m),

 …………………

 N_l = N_k-1 - n∙p, (N_ln∙p), l, n, p, m, k Z. То Nn тільки тоді, якщо N_ln.

Приклад 2.2.1. Використовуючи модифікований рекурентний спосіб подільності, перевірити чи ділиться 123459 на 7.

Розв’язання: Послідовно віднімаємо від числа 123459 – 70000, 7000, 700, 70, 7 в залежності від кількості цифр заданого числа, або різниці, маємо:

123459 – 70000 = 53459 

53459 – 7000 = 46459  46459 – 7000 = 39459  39459 – 7000 = 32459  …  42 – 7 = 35  35 – 7 = 28  28 – 7 = 14  7 7, отже 123459 7.

Зрозуміло, що цей алгоритм цікавий, але трудомісткий, а, отже, далеко не  ефективний, тим паче, що для 7 є раціональніші ознаки подільності.

 

 2.3. Встановлення ознак подільності шляхом розбивання числа на одно, двох і трьохзначні грані справа наліво

 

 2.3.1. Ознаки подільності числа на 3, 9

Виведемо ознаки подільності числа N на 3 і 9.

 Представимо число N як N=10ⁿа_n + 10^n-1а_n-1 + … +  10²а₂ + 10а₁ + а₀

де 0a_i< 10.

 Тоді число N можна записати так

 Отже, число N ділиться на 3 або 9 тоді і тільки тоді, коли сума цифр даного числа ділиться на 3 чи 9 відповідно.

Теорема 2.8.

                     ; 

 

 

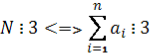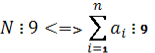
Приклад 2.3.1.1. Чи ділиться на 3 і на 9 число, яке записується 4444-ма четвірками?

Розв’язання: Сума цифр числа А дорівнює 44444=17776. Застосовуючи до одержаного числа ознаку подільності на 3 і 9 переконуємося, що 17776 не ділиться на 3 і 17776 не ділиться на 9.

 Отже, це число не ділиться без остачі на 3 і 9.

2.3.2. Ознака подільності на 11

2.3.2.1. Запишемо число N у вигляді N=10²ⁿа_n + 10^2n-2а_n-1 + … +  10²а₁ + а₀

де 0a_i< 100. Таке представлення числа N відповідає умовному розбиванню даного числа на двозначні грані справа наліво. Тоді N можна записати так:

Звідси N 11, якщо де a_i – двозначне число утворене розбиттям N на двозначні грані справа наліво.

Теорема 2.9. Число розбивають на двозначні грані справа наліво (якщо необхідно, дописуємо 0 в кінець або початок числа). Якщо сума отриманих граней ділиться на 11, то і саме число ділиться на 11

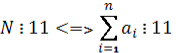                                                                                                 де a_i – двозначне число.

Приклад 2.3.2.1.1. Чи ділиться націло на 11 число 9163627?

Розв’язання:27 + 36 + 16 + 09  = 88  
88 11, тому 9163627 11.

2.3.2.2. Друга ознака подільності на 11 базується на різниці однозначних граней, що стоять на парних та непарних місцях.

Теорема 2.10. Якщо число розбити на однозначні грані і сума граней, що стоять на непарних місцях дорівнює сумі граней, що стоять на непарних місцях, або їх різниця ділиться на 11, то і число ділиться на 11.
, якщо 11

  Доведення:Нехай N=10ⁿа_n + 10^n-1а_n-1 + … +  10²а₂ + 10а₁ + а₀

Врахуємо, що 10¹ -1 (mod 11), 10³ -1 (mod 11), …, 10^2k+1 -1 (mod 11), а  10² 1 (mod 11), 10⁴ 1 (mod 11), …, 10^2k 1 (mod 11). Приходимо до висновку, що 11, при умові, що 11.

Приклад 2.3.2.2.1. Чи ділиться 9163627 на 11.

Розв’язання: 7 – 2+6 – 3+6 – 1+9=22, 22ділиться на 11, отже, 9163627  ділиться на 11.

Другий спосіб визначення подільності числа N на 11 більш зручний, порівняно з першим. Адже доводиться мати справу з меншими числами, а, отже, швидше отримується кінцевий результат.

2.3.3. Ознака подільності на 7 і 13

 Ідея розбиття числа N на трьохзначні умовні грані знайшла своє застосування при визначенні ознак подільності числа N на 7 та 13.

 Неважко помітити, що

  10³ = 1000 = 143 ∙ 7 – 1  10³ = 77∙13 – 1

  10⁶ = 142857∙7 + 1  10⁶ = 76923∙13 + 1

 Тому 10^2n-1 -1 (mod 7), а 10²ⁿ 1 (mod 7)

Отже,  запишемо число N у вигляді:

 N=10³ⁿа_n + 10^3n-3а_n-1 + … +  10⁶а₂ + 10³a₁ + а₀, де 0a_i< 1000.

Таке представлення числа N відповідає умовному розбиванню даного числа на тризначні грані справа наліво.                                                                              

 Теорема2.11.7,13тоді і тільки тоді, коли 7,13, 0a_i< 1000

2.3.4. Ознака подільності на 37

 Як і в попередньому випадку, розділимо число N на тризначні грані справа наліво, тобто N=10³ⁿа_n + 10^3n-3а_n-1 + … +  10⁶а₂ + 10³a₁ + а₀. Так як 1000 = 27 ∙ ∙37 + 1, тоді 10^3k 1 (mod 37). Отже, має місце таке твердження:

Теорема 2.12.N=(10³ⁿа_n + 10^3n-3а_n-1 + … +  10⁶а₂ + 10³a₁ + а₀) 37 тоді і

тільки тоді, коли +, де a_i– тризначні числа, утворені в результаті поділу даного числа на тризначні грані, починаючи справа наліво.

Приклад 2.3.4.1. Визначити подільність числа 29583794 на 7, 11, 13, 37, користуючись методом розбиття числа N на тризначні грані справа наліво.

Розв’язання: 794 – 583 + 29 = 240. 240 не ділиться націло на 7, 11, 13. Отже, 29583794 не ділиться націло на 7, 11, 13.             
Визначимо подільність даного числа на 37. 
794 + 583 + 29 = 1406. 1 + 406 = 407 37, отже N 37.

Оригінальність цього методу очевидна, тим більше, що він дає можливість визначати подільність числа на 37, яка не виводилася за допомогою методів, що розглядалися вище

   2.4. Ознаки подільності чисел  виду 10n + 1, 10n – 1

У 1884 році в одному з номерів  “Журналу елементарної математики”, який видавався у Києві, була поміщена стаття засновника журналу В.П.Єрмакова  “Ознаки подільності чисел ”. В статті було поміщено ознаки подільності чисел виду 10n+1,10n – 1.

Щоб встановити,чи ділиться дане число N на число m =10n+1, потрібно:

А. відкинути від числа N останню цифру;

Б. відняти від отриманого числа добуток відкинутої цифри на n;

В. з отриманим числом виконати операції А і Б;

Г. робити це до тих пір, поки не залишиться число менше,або рівне 0

Д. якщо число, що залишилося 0, то  N ділиться на  m =10n+1; у противному випадку N не ділиться на m.

                                                 А          Б         А       Б      А      Б

Приклади  N = 11934. m = 51.    1193 4→1193→1173→117→102→10→0

                    N = 15314. m = 61.      1531 4→1531→1507→150→108→10→-38

Ми бачимо, що 11934 ділиться на 51, а 15314 не ділиться на 61.
зауважимо. Що якщо у випадку подільності записати відкинуті цифри в оберненому порядку, то отримаємо частку; наприклад, 11934:51= 234.

Щоб отримати ознаку подільності на  m =10n – 1,необхідно в Б замінити віднімання додаванням, в Г і в Д  замість 0 написати  m, а замість 10n+1 написати  10n – 1.                                     

 

                                                                      А         Б       А     Б      А      Б

Приклади  N = 9246. m = 69.        924 6→924→96 6→96→13 8→13→69   (тут операція  Б – це змінена операція Б). Значить 9246 ділиться на 69.

За допомогою ознак подільності можна навести простіші теореми про подільність .

1.Якщо a ділиться на b,  b ділиться на с, то а ділиться на с,  т.т. якщо а =сq   та  b= сq , то а = сq′.

2 Якщо кожне з чисел а та b ділиться на с, то сума  їх ділиться на с, т.т. а =сq   та  b= сq , то а + b = сq.

Ознака подільності суми. Якщо кожен із доданків ділиться на натуральне число b, то і сума ділиться на b.

3. Якщо кожне з чисел а та b ділиться на с, то різниця  їх ділиться на с,

т.т. а =сq   та  b= сq , то а - b = сq.

Ознака подільності різниці.. Якщо зменшуване та від’ємник ділиться на натуральне число b, то і різниця  ділиться на b.

4.Ознака подільності добутку. Якщо хоч один із співмножників ділиться на натуральне число b, то і добуток ділиться на b.               

 

 

 

2.5.  Таблиця подільності    (Додаток  А,таблиця )  .                                      

 

 

 

 

 

 

                                                        РОЗДІЛ 3

               ЗАСТОСУВАННЯ ОЗНАК ПОДІЛЬНОСТІ НА ПРАКТИЦІ

 

3.1. Приклади  розв’язування задач на використання ознак   подільності                       

 1.Знайдіть найбільше парне трицифрове число

 Розв’язання :

Найбільше трицифрове число 999 – непарне. Йому передує число 998.Отже найбільше парне трицифрове число  998.

Відповідь: найбільше парне трицифрове число  998.

2.Знайдіть  найбільше  чотирицифрове число, яке кратне 3, але не кратне Розв’язання :

Найбільше  чотирицифрове число 9999  - непарне. Воно ділиться і на 3 і на 9.Якщо це число зменшити на 3. то воно стане 9996 і  буде кратним числу 3, але не кратне 9.

Відповідь: найбільше  чотирицифрове число,яке кратне 3,але не кратне 9  є  9996.

3.Знайдіть серед чисел виду 3n + 1 три числа,  кратні 5

 Розв’язання :

Для того,щоб число виду 3n + 1 ділилося на 5. необхідно,щоб остання цифра в записі цього числа була 0 або 5. Нехай ці числа закінчуються 0,тоді числа виду 3n повинні закінчуватися на 9 і ділитися на 3.Розглянемо деякі з них, що задовольняють першу вимогу  9, 19, 29,39, 49,59,69…Виберемо з них ті, що задовольняють і другу вимогу.9, 39,69.Отже серед чисел виду 3n + 1 на 5 діляться числа: 9 +1 = 10, 39 + 1 = 40, 60 + 1 =70.

4.Число a+2 ділиться на 5

Довести:   3a+16 також ділиться на 5

Розв’язання :

3a+16=3a+6+10=3(a+2)+10

Кожен з доданків ділиться на 5, то й вся сума ділиться на 5.

 5. Нехай a, b – натуральні числа, причому сума 6a+11 b  ділиться на    31.

Довести:   що тоді число a+7 b також ділиться  на 31

 Розв’язання :

Розглянемо добуток (a+7 b)×6=6a+42 b=( 6a+11 b)+31 b

(a+7 b)*6 – ділиться на 31, то й  ( 6a+11 b)+31 b ділиться на 31

Отже, додаток 6a+11 b повинен ділитися на 31.

6.Довести, що число 378 + 9 ділиться на 10  без остачі.

Розв’язання :

78 закінчується  1 , а 9 + 1 = 10. отже дане число ділиться на 10.

7. Довести, що сума п’яти  послідовних непарних чисел ділиться на  5.

 Розв’язання :

Число ділиться на 5, якщо воно закінчується 5 або 0 Непарні послідовні числа позначимо 2n-3; 2n-1; 2n+1; 2n + 3; 2n +5.Знайдемо їх. суму

 2n-3+ 2n-1+ 2n+1 + 2n + 3 + 2n +5 = 10 n +5 = 5 ( 2 n + 5 ) ділиться на 5, бо один із множників 5 , а він ділиться на 5.

9. Довести, що сума п’яти  послідовних  цілих  чисел ділиться на 5.

 Розв’язання :

Число ділиться на 5, якщо воно закінчується 5 або 0. Послідовні  цілі числа позначимо n-3; n-2; n - 1; n ; n +1.Знайдемо їх. суму

n -3 + n-2 +n – 1 + n  + n +1 = 5 n  - 5 =5 ( n  - 1 ) ділиться на 5.бо 5 : 5.

 10.  На дошці написано число   321321321321.Які цифри треба стерти, щоб отримати  найбільше можливе число, яке ділиться на 9 ?

Розв’язання: для розв’язання задачі скористаємося ознакою подільності натуральних чисел на 9 : на 9 діляться ті і лише ті натуральні числа, сума цифр яких ділиться на 9. Сума цифр даного числа  а = 321321321321 становить 24.

Найбільшим натуральним числом, яке не перевищує 24 і ділиться на 9, є число 18. Оскільки 24 – 18 = 6, то в даному числі слід закреслити такі цифри, сума яких становить 6. Очевидно,що шукане число буде найбільшим, коли буде закреслена найменша кількість цифр. Оскільки в даному числі

а = 321321321321 зустрічаються виключно цифри 1, 2 і 3( кожна точно чотири рази), то найменша кількість цифр, що закреслюються у числі і сума яких дорівнює 6, становить 2.Тобто, коли видаляються точно дві трійки. Отже, шукане число одержується із заданого в результаті закреслювання двох трійок. Оскільки в даному числі рівно чотири трійки ( що займають 1-шу, 4 – ту, 7–му та 10-ту позиції), то існує точно 6 різних способів закреслювання двох зазначених трійок. Шукане число буде найбільшим в тому випадку, коли будуть викресленими трійки,що займають 7-му і 10-ту позиції, тобто ті, що відповідають меншим розрядним одиницям. Отже шуканим числом є число   321321321321  = 3213212121

Відповідь: 3213212121

 

 

 

 

 

3.2.Задачі на застосування ознак подільності

• Яку найбільшу кількість однакових букетів можна скласти із 24 волошок і 32 ромашок, використавши всі квіти?
• Прямокутний паралелепіпед, що має довжину 42 см, ширину 30 см і висоту 18 см, розрізали на однакові найбільші куби. Скільки утворилося таких кубів?
• Прямокутний аркуш паперу завдовжки 56 см і завширшки 48 см потрібно розрізати без відходів на найменшу кількість рівних квадратів. Скільки квадратів одержимо?
• Дерев'яний брусок завдовжки 48 см, завширшки 30 см і заввишки 24 см потрібно розрізати без відходів на найменшу кількість рівних кубів. Скільки кубів одержимо?
• Яку найбільшу кількість однакових подарунків можна скласти з 90 мандаринів, 405 цукерок і 135 пряників, якщо потрібно використати всі мандарини, цукерки і пряники?
• Між усіма учнями класу розділили порівну 58 зошитів у лінійку і 87 зошитів у клітинку. Скільки учнів у класі? Скільки зошитів у лінійку і скільки у клітинку отримав кожен учень?
• У кімнаті завдовжки 625 см і завширшки 475 см вирішили викласти долівку однаковими декоративними плитками квадратної форми, не розрізуючи їх. Який найбільший можливий розмір такої плитки? Скільки плиток найбільшого розміру потрібно, щоб викласти ними долівку?
• У Петрика було більше ніж 30, але менше ніж 50 камінчиків. Коли він розклав камінчики у купки по 5 штук, то один камінчик залишився, а коли він розклав їх у купки по 3 штуки, то залишилось 2 камінчики. Яка кількість камінчиків була в Петрика?
• Було 5 аркушів паперу. Деякі з них розрізали на 5 шматків кожен. Таку операцію розрізування повторили кілька разів. Чи можна в результаті таких операцій отримати 2015 шматків?

 

                                                       ВИСНОВОК

У результаті проведеного дослідження  я   прийшла  до таких висновків:

• Тема “Ознаки подільності чисел ” є актуальною, тому що  вона вивчається й використовується у шкільній програмі, у завданнях  математичних олімпіад. Я вважаю, що треба знати  хоча б основні ознаки подільності чисел, щоб потім їх застосовувати при розв’язуванні задач на подільність;
• Необхідність введення ознак подільності  була викликана потребою  визначати,  чи ділиться одне число на інше, не виконуючи самого ділення;
•  Я  дослідила  близько 40 ознак подільності чисел. Основне значення ознак подільності  для практичних застосувань складається в їхній простоті для запам’ятовування. Більшість ознак виходять із основних простіших ( на 2, 3, 4, 5, 11).Частина ознак подільності мають по 2  та 3 ознаки подільності на одне й те число, але різні за змістом. Знаючи основні ознаки, ми можемо вивести інші ( на12\25\14\28). 
• За допомогою досліджених ознак я можу  розв’язувати завдання на ділення чисел набагато швидше і зручніше,  знаючи  тільки табличку множення;
• Ознаки подільності можуть бути корисними  не лише при розв’язуванні задач, а й стати підґрунтям для демонстрації числових фокусів. Ось один із них: фокусник просить одного з глядачів, у якого є коробочка сірників, порахувати їх, потім витягти з коробочки кількість сірників, яка дорівнює сумі цифр отриманого числа. Не повідомляючи ніякої інформації, глядач передає фокуснику закриту коробочку. Той деякий  час трясе її і, не відкриваючи, визначає кількість сірників у коробці.

          Тут не має ні магії. ні чародійства. Просто фокусник добре знає ознаку подільності на 9, з якої випливає, що різниця числа і суми його цифр завжди

ділиться націло на 9. А отже,у коробочці може бути лише 9,18,27,36 або 45 сірників ( зазвичай у коробочці більше не буває). Зважаючи на це, при певному тренуванні  можна за звуком ( або за масою коробочки) визначити кількість сірників.

•   При написанні роботи я систематизувала  матеріал про подільність чисел, дізналась багато нового, а також удосконалила  та поглибила знання з даної теми. Вмію розв’язувати нескладні олімпіадні завдання на подільність чисел;
• Планую продовжити займатися дослідженням даної теми, спробую розв’язувати завдання підвищеної складності на подільність чисел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                        СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.Астахов Ю.Н. и др. Кибернетика и энергетика , Москва  “Знание“, 1967

2.Бевз Г.П., Бевз В.Г. Математика, 6 клас. Київ, “ Генеза ”, 2006.

3. Бевз Г.П.  Математика, 6 клас.  Київ, “ Вежа ”, 2002.

4. Бородін О.І   Теорія чисел.   Київ  « Виша школа», 1970

5.Выгодский М.Я.  Справочник по элементарной математике  Москва.

 “ Наука”, 1986.

6.Глушков В.М. та ін. Бесіди про управління. Київ, Політвидав України,1973 7. Грибанов В.У.Сборник упражнений по теории чисел,  ,Москва. “Просвещение”, 1984.

8.Конфорович А.Г., Андрощук І.Г., Груніна К.О. Математичні вечори у восьмирічній школі. Київ,   “ Радянська школа ”,   1974.

9.Мерзляк А.Г.,Полонський В.Б.,Якір М.С.  Математика, 6 клас,  Харків

“ Гімназія” , 2006.

10. О.Г.Черватюк, Г.Д.Шиманська  Елементи цікавої математики на уроках математики. Київ, “ Радянська школа ”,  1968

 11.Газета  “ Математика”,  № 748, №749   “Шкільний світ ”,  2014

 12. Журнал “ Квант ”, № 4 . “ Наука”, 1987р.

 

 

 

 

 

                                                    Додаток А

Таблиця подільності

 

              Таблиця подільності

               Таблиця     2.5.1.

Дільник	Умова     подільності	Приклади
2	Остання  цифра є парною	1,294: 4 є парне.
3	Сума цифр повинна ділитися на 3.	9405: 4 + 0 + 5 =. 9
4	1) Число, утворене двома останніми цифрами ділиться на 4 .2) Половину розряду одиниць додати до десятків, якщо сума ділиться на 2,або закінчується 0,то число ділиться на 4.	2,092: 92 ділиться на 4. 9+1=10       189468              8:2=4   (4+6 ) :2, то число : 4
5	Остання цифра або 5, або 0.	490: остання цифра 0.
6	Якщо число ділиться і на 2, і на 3.( парне і сума цифр ділиться на3.)	24 ділиться на 2 і на 3.
7	1) Число розбивається  по три цифри, починаючи з кінця.   Різниця суми   блоків, що стоять на парних місцях і суми блоків, що стоять на непарних місцях, ділиться на 7 2) Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7.                3) Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7.                4) Різниця між числом без останньої цифри і подвоєної останньої цифри повинна ділитись на 7.	2,911,272:    911 - (2 + 272) = 637. 637 :  на 7 689255,   689.255         689-255=434:7 364: (3x2) + 64 = 70. 70 ділиться на 7.   364: 36 + (5×4) = 56. 56 ділиться на 7.   364:  36 − (2×4) = 28. 28 ділиться на 7.
8	1) Якщо число, утворене останніми трьома цифрами, ділиться на 8. 2)коли три останні цифри нулі.	5,128: 128 ділиться на 8.
9	Сума всіх цифр повинна ділитись на 9.	2,880:  2 + 8 + 8 + 0 = 18.
10	Остання цифра 0.	130: остання цифра 0.
11	1) Число розбивається на блоки по дві цифри, починаючи з кінця. Сума блоків повинна ділитись на 11. 2) Якщо різниця між числом без останньої цифри і останньою цифрою ділиться на 11. 3) Якщо сума цифр, що стоять на парних місцях відрізняється від суми цифр, що стоять на непарних місцях, починаючи з кінця, на число, що кратне 11.	627: 6 + 27 = 33. 33     627: 62 - 7 = 55. 55   182919:   (9 + 9 + 8) - (1 + 2 + 1) = 22.
12	1) Якщо число ділиться на 3 і на 4.    2) Число без останньої цифри множать на два і віднімають останню цифру. Таке число повинне ділитись на 12.	324: ділиться  на 3  і  4. 324: (32x2) − 4 = 60. 60 ділиться на 12.
13	1) Число ділиться на блоки по три цифри, починаючи з кінця. Сумують блоки, що стоять на парних і непарних місцях. Різниця цих сум повинна ділитись на 13.              2) До числа без останньої цифри додають останню цифру, помножену на 4. Утворене число повинне ділитись на 13.                3)  Від числа без останньої цифри віднімають останню цифру, помножену на 9. Утворене число повинне ділитись на 13.	2,911,272: 911 - (2 + 272) = 637. 637 ділиться на     338: 33 + (8×4) = 65. 65 ділиться на 13. 637: 63 − (7×9) = 0. 0 ділиться на 13.
14	1) Якщо число ділиться на 2 і на 7 2) Число без останніх двох цифр множать на 2. До результату додають число, утворене двома останніми цифрами. Сума повинна ділитись на 14.	224: ділиться  на 2 і на7. 364: (3x2) + 64 = 70.
15	Якщо число ділиться на 3 і на 5	390: ділиться на 3 і на 5.
16	1) Якщо число тисяч є парним, то перевіряють число, складене з останніх трьох цифр.                2) Якщо число тисяч є непарним, то до числа, утвореного останніми трьома цифрами, додають 8 і результат  ділиться на 16. 3) Число без останніх двох цифр множать на 4 і додають число, утворене останніми двома цифрами. Результат повинен ділитись на 16.	254,176: 176 ділиться на 16.   3408:    408+8 = 416. 416 ділиться на 16.    176: (1x4) + 76 = 80. 80 ділиться на 16.
17	1) Число без останніх двох цифр множать на 2 і додають число, утворене останніми двома цифрами. Результат повинен ділитись на 17.                2) Від числа без останньої цифри віднімають останню цифру, помножену на 5. Результат повинен ділитись на 17.	187: − (1x2) + 87 = 85. 85 ділиться на 17.     85: − 8 + (5×5) = 17.
18	Якщо число ділиться на 2 і на 9.	342:  ділиться на 2 і на 9.
19	До числа без останньої цифри  додають подвоєну останню цифру. Результат повинен ділитись на 19.	437: 43 + (7x2) = 57. 57 ділиться на 19.
20	1) Якщо число ділиться на 10 і число десятків є парне.  2) Якщо число, утворене двома останніми цифрами ділиться на 20.	360:  число ділиться на 10 і 6 є парним. 480:  80 ділиться на 20.
21	Якщо число ділиться на 3 і на 7	2911272:    911 - (2 + 272) = 637. 637   :  7,  2+9+1+1+2+7+2=24 : 3
22	Якщо число закінчується на парну цифру й ділиться на 11.	6886: ділиться на 11 і закінчується парним
23	Число ділиться на 23 тоді й лише тоді, коли число його сотень, складене з потроєним числом десятків і одиниць, кратне 23.	23184   1+3×84=253:23
24	Якщо число ділиться на 4 і на 2 і на 3	134280 : 24
25	1) Якщо число, складене з двох останніх цифр, ділиться на 25. 2) Коли число, утворене його останніми двома цифрами, ділиться на 25,або останні його цифри 00.	134,250: 50 ділиться на 25. 134275 : 25,бо 75 : 25
27	1) Число ділять на блоки по три цифри, починаючи з кінця. Сума утворених блоків повинна ділитись на 27.                2) Від числа без останньої цифри віднімають  останню цифру, помножену на 8.	2,644,272: 2 + 644 + 272 = 918. 918 ділиться на 27. 621: 62 − (1×8) = 54. 54 ділиться на 27
30	Якщо число ділиться на 3,  на 5  і є парним	134250: 30
32	1) Якщо число десятків тисяч є парним, то перевіряють на подільність число, утворене останніми чотирма цифрами.                  2) Якщо число десятків тисяч є непарним, то до числа, утвореного останніми чотирма цифрами, додають 16.                3) Число без останніх двох цифр множать на 4 і до результату додають останні дві  цифри. Суму перевіряють на подільність на 32.	41,312: 1312 ділиться на32   254,176: 4176+16 = 4192. 4192 ділиться на 32.   1,312: (13x4) + 12 = 64.
33	1)Якщо число ділиться на 11 і на 3.  2)Число ділять на блоки по дві цифри, починаючи з кінця. Утворені блоками числа сумують. Результат повинен ділитись на 3 і 11	1,003,002  :  на 11 і на 3. 627 ;   6 + 27 = 33.
34	Якщо число ділиться на 17 і  на 2	170 : 34,  374 : 34
35	Якщо число ділиться на 7 і  на 5	689255, 689-255=434:7
37	1) Число ділять на блоки по три цифри, починаючи з кінця. Числа, утворені блоками сумують. Сума повинна : на 37.                2) Від числа без останньої цифри віднімають останню цифру, помножену на 11. Результат повинен ділитися на 37.	2,651,272: 2 + 651 + 272 = 925. 925 ділиться на 37. 925: 92 − (5x11) = 37.
49	До числа без останньої цифри додають останню цифру, помножену на 5. Таке число повинне ділитись на 49.	1,127:  112 + (7×5) = 147. 147 ділиться на 49.

 

 

 

 

 

 

 

 

 

 

                                                      ВІДГУК КЕРІВНИКА

 

 

на науково-дослідницьку роботу« Ознаки подільності.та їх застосування » Овчаренко Дарії Юріївни,     учениці 8 класу       Григоро - Бригадирівської загальноосвітньої школи І-ІІ ступенів,  Кобеляцького району, Полтавської області

       Робота Овчаренко Дарії є досить актуальною, як з теоретичної, так і практичної точки зору. Учениця добре розкрила питання «Ознаки подібності».

Вибір теми дослідження був свідомий і аргументований. Учениця опрацювала достатню кількість додаткової літератури, а також інформації в мережі інтернет. В процесі роботи значно поглибила свій рівень знань з даного питання, розширила кругозір, навчилася  працювати творчо та самостійно.

Зміст основної частини точно відповідає темі та повністю розкриває її. Результати досліджень відповідають меті.

Учениця добре попрацювала з різними джерелами інформації. Творчо використала опрацьований матеріал, зробила аргументовані висновки.

    Робота написана грамотно і відповідає стилю оформлення тексту рукописних робіт.   Зі своєю роботою учениця  виступила перед  однокласниками.

     Науковий керівник : Мирошниченко Алла Миколаївна, вчитель математики і  фізики , спеціаліст вищої категорії, Григоро – Бригадирівської загальноосвітньої                     школи І-ІІ ступенів, Кобеляцького району , Полтавської області.