Розробка уроку алгебри в 7 класі на тему: «Лінійне рівняння з однією змінною»

Розробка уроку алгебри в 7 класі на тему: «Лінійне рівняння з однією змінною»

Тема. Лінійне рівняння з однією змінною

Мета: освітня: поглибити, розширити й узагальнити відомості про види рівнянь та способи їх розв’язування; домогтися свідомого розуміння змісту поняття «лінійне рівняння з однією змінною» та алгоритму розв’язання лінійних рівнянь;

розвиваюча: розвивати вміння лаконічно та грамотно висловлювати свою думку, допитливість, жадобу до знань;

виховна:формувати науковий світогляд, виховувати кмітливість, наполегливість потребу в праці.

Тип уроку: засвоєння нових знань.

Обладнання: комп’ютер, проектор,роздатковий матеріал, картки самооцінювання, підручник.

Очікувані результати:

Після  уроку учні зможуть:

• cистематизувати свої знання про рівняння з однією змінною;
• співпрацювати;
• вчитися відповідно оформляти записи розв’язку рівнянь;
• поглибити вміння оцінювати свої знання.

Епіграф до уроку:

«Узагальнення-це, мабуть, найлегший і найочевидніший шлях розширення математичних знань.»

В.Сойер

Хід уроку

І. Організаційний етап.

Привітання з класом, вчитель перевіряє готовність учнів до уроку. Оголошується конкурс «Зразковий стіл» серед учнів, які сидять за однією партою, на кращу підготовку навчального приладдя та навчальних посібників до уроку. За результатами конкурсу оголошується «Зразковий стіл» (їх може бути декілька). Учитель попереджає учнів про заповнення талонів самооцінювання.

ІІ. Робота із випереджальним домашнім завданням.

На дошці записане завдання.

Серед математичних записів один зайвий. Поясніть, який та чому?

1)3х+2=5;  2)3+2=5;  3)3+2=5х;  4)3х+2х=5.

Учням можна поставити завдання:

1)знайдіть відмінності між цими записами;

2)знайдіть схожість у цих записах;

3)сформуйте групи за ознакою схожості;

4)дайте означення утвореним групам.

Після проведеної роботи учні ще раз усвідомлюють, що рівність з невідомим значенням букви називають рівнянням з одним невідомим (або рівнянням з однією змінною).

III. Мотивація пізнавальної діяльності. Бесіда.

Як довго ви вивчали рівняння? (Очікувана відповідь: від першого по шостий клас). Пригадайте прості правила, які ви вивчали ще в молодших класах і за якими ми можемо знайти невідомий компонент рівняння. (Учні розповідають правила знаходження невідомого доданка, множника і т. д.). У 6 класі ви вивчили основні властивості розв’язання рівнянь. Згадайте їх після «трансляції» реклами.

Увага!   Увага!

-За виконання своєї місії береться АЛГЕБРА. У неї спецзавдання: розшукати учнів 7 класу і навчити їх розв’язувати рівняння.

-У АЛГЕБРИ трапилося нещастя: правила розв’язування рівнянь розгубилися. Давайте їй допоможемо.

• Розкриття дужок.
• Знаходження значення змінної.
• Зведення подібних доданків.
• Перенесення невідомих членів рівняння в одну частину, а відомих членів рівняння в іншу, змінюючи при цьому знак на протилежний.

(Учні впорядковують ці правила).

Застосування основних властивостей значно полегшує розв’язування багатьох рівнянь. Епіграфом до уроку є слова Сойера «Узагальнення – це, мабуть, найлегший і найочевидніший шлях розширення математичних знань».

Тема нашого уроку «Лінійне рівняння з однією змінною». Це продовження матеріалу про рівняння з 6-го класу та одночасне розширення ваших знань. На цьому уроці ми вивчимо алгоритм розв’язування рівнянь, що називаються лінійними.

IV. Сприймання і усвідомлення нового матеріалу.

Пояснення учителя супроводжуються презентацією.

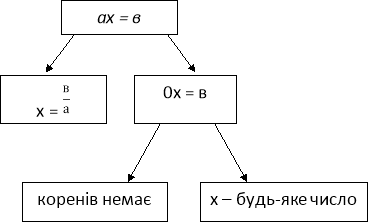
Слайд 1. Означення лінійного рівняння. Рівняння вигляду ax=b,де а і  b - деякі  відомі  числа, х- змінна, називається лінійним рівнянням. Ліва частина цих рівнянь – добуток числа і змінної, права частина—будь-яке число. Числа a I b називають  коефіцієнтами рівняння. Наприклад: 2х=-4;   0,25х=0;   х=1.

Учні усно виконують вправу №40 (Кравчук В. Алгебра. Підручник для 7 класу / В. Кравчук, Г. Янченко. – К. – Тернопіль: Підручники і посібники, 2007. –ст. 15,[1]) та наводять свої приклади. Використовується інтерактивна вправа «Мікрофон».

Щоб дати відповідь на питання «Скільки коренів має лінійне рівняння?», учням пропонується виконати №41 ([1]).

1.               56х=64,             2) 0х=-2,                                3) 8х=0,               4) 0х=0.

  х= ,               не має коренів                        х=,                   безліч коренів

х=.                                   х=0.

Робиться висновок: кількість коренів лінійного рівняння залежить від значень коефіцієнтів лінійного рівняння.

Слайд 2.Схема розв’язання лінійного рівняння ах=в.                                                         якщо                                            а 0     а = 0                                          1 корінь                 якщо                                                                   в 0                                                                                            безліч коренів
Слайд 3. Алгоритм розв’язку лінійного рівняння. Позбутися знаменників. Розкрити дужки. Перенести члени зі змінними в ліву частину рівняння, а інші-у праву. Звести подібні доданки.

Цей алгоритм базується на застосуванні основних властивостей рівнянь. Отже, в результаті проведених перетворень дістаємо рівняння, рівносильне даному.

Розглянемо приклад:

                                     7(0,3х-2)-9(0,9х-1)=2х-1,

                                       2,1х-14-8,1х+9=2х-1,

                                                 -6х-5=2х-1,

                                                 -6х-2х=-1+5,

                                                       -8х=4,

                      х=,

                    х=-0,5.

 Відповідь:х=-0,5.

Фізкультхвилинка. Рухлива вправа «Як живеш?». Учасники стають у коло. Учитель запитує учнів, а вони голосно йому відповідають і підтверджують свої слова рухами.

-Як живеш?

- Ось так!(Піднімають великий палець правої чи лівої руки вверх.)

- Як ідеш?

- Ось так! (Крокують на місці, піднімаючи високо коліна.)

- Як танцюєш?

- Ось так! (Танцюють.)

- Як береш?

- Ось так! (Широкий жест до себе.)

- Як даєш?

- Ось так! (Широкий жест від себе.)

- Як зірки з неба зриваєш?

- Ось так! (То правою, то лівою рукою тягнуться догори).

V. Узагальнення і систематизація вивченого матеріалу.

Інтерактивна вправа «Робота в малих групах»

Учні об’єднуються у групи по 3 особи (сильний, середній і слабкий учні). Це необхідно для стимулювання творчого мислення й інтенсивного обміну ідеями. Кожна група працює над своїм завданням. Учитель контролює процес. Необхідно домогтися, щоб усі учні зрозуміли, як виконується завдання. По закінченні відведеного часу кожна група представляє результати своєї роботи. Вчитель здійснює перевірку за готовим трафаретом.

Завдання для групи 1.

1. Розв’яжіть рівняння:

7х+32=12х+25.

2^. Розв’яжіть рівняння:

2(х-11)-5(5-2х)=-23.

3. При якому значенні змінної х значення виразів 11(3х-7) і 13х-2 рівні між собою.

Завдання для групи 2.

1. Розв’яжіть рівняння:

4-3х=6х+22.

2^. Розв’яжіть рівняння:

8(-3х+4)+14(3+2х)=4+2х.

3. При якому значенні змінної х значення виразів 13(2х-8) і 20х-200 рівні між  собою.

Завдання для групи 3.

1. Розв’яжіть рівняння:

14-х=19-11х.

2^. Розв’яжіть рівняння:

-5(4х+3)+3х=-12(х-3).

3. При якому значенні змінної х значення виразів 5(2х+1) і 2(4х+3) рівні між собою?

Відповіді до завдань.

	Завдання для групи 1	Завдання для групи 2	Завдання для групи 3
1	1,4	-2	½
2	2	-35	-10,2
3	3,75	-16	½

VI. Підсумок уроку.

У картках самооцінювання зробимо підбиття підсумків роботи у групах. Підкресліть вибране.

1.                   Чи кожен учень зміг висунути свою пропозицію?

Так.         Не зовсім.       Ні.

2.                   Чи все обговорили?

Так.         Не зовсім.       Ні.

3.                    Чи виконали завдання до кінця?

Так.         Не зовсім.       Ні.

1.                 Підбиття підсумків роботи вчителем.

Учитель звертає увагу на те: яка група швидко і правильно виконала завдання; як працював весь клас; як працювали окремі учні.

VII.Домашнє завдання.

Обов’язковий рівень.

1.       Вивчити п. 3. [1].
2.       Розв’язати вправи №47 [1, ст.16]

Високий рівень.

1.        Розв’язати вправу №52[1, ст.17]
2.        Пояснити фокус М.Ю. Лермонтова

Математична забава М.Ю. ЛЕРМОНТОВА

М. Ю. Лермонтов був не тільки великим поетом, а ще й військовим та захоплювався математикою.

Під час відпочинку Лермонтов запропонував фокус:

•       Задумайте яке завгодно число. За допомогою простих арифметичних дій я визначу його.
•       Добре, задумав, – сказаводин з офіцерів, які стояли навколо нього.
•       Додайте до нього ще 25. Тепер чи не завгодно додати до нього ще 125? Відніміть36. Ще відніміть число, що ви задумали. Помножте залишок на 5. Отримане число поділіть на 2. Подивимось що у вас вийшло? Якщо не помиляюся, число 285?

Офіцер навіть підскочив, так уразила його точність обчислення:

•       Так, цілком правильно!

Подумайте: на чому засновано фокус?

(х+25+125-36-х)×5:2=285

 

2.2.3.Розробка уроку алгебри в 8 класі на тему: «Формула коренів квадратного рівняння». Урок-ділова гра «Компетентність»

Тема.Формула коренів квадратного рівняння. Урок-ділова гра «Компетентність»

Мета:освітня: узагальнити, систематизувати та поглибити набуті знання, навички та вміння розв’язувати квадратні рівняння за формулою коренів;

розвиваюча:розвивати культуру математичної мови, пізнавальні мотиви, бажання бути першим;

виховна:формувати пізнавальну, особистісну,самоосвітню, соціальну, творчу компетентності; виховання свідомості, спрямованої на визнання високої соціальної значущості плідної праці людини; .

Тип уроку: застосування знань, умінь і навичок.

Обладнання: математичний кросворд, картка самоконтролю,комп’ютер, презентація, роздатковий матеріал.

Очікувані результати:

Після уроку учні зможуть:

• оперувати знаннями з теми «Квадратні рівняння»;
• об’єктивно оцінювати свої можливості;
• проводити самоконтроль власної діяльності;
• працювати в команді;
• розвивати ініціативу, самостійність, соціальні компетентності.

Хід уроку

І. Організаційний етап. Перевірити готовність учнів до уроку.

Інтерактивна вправа «Світлофор настрою».

У кожного учня сигнальна картка, один бік якої зелений, а другий – червоний.

Учитель. Діти, покажіть за допомогою світлофора, з яким настроєм ви прийшли сьогодні на урок. (Учні піднімають сигнальні картки). Я бажаю вам, щоб гарний настрій не залишав вас до кінця уроку. Якщо ж настрій не дуже вам подобається, намагайтеся працювати на уроці так, щоб він покращився.

II. Мотивація навчальної діяльності.

Тема нашого уроку «Розв’язування квадратних рівнянь за формулою коренів». Видатний французький математик Жан Лерон Д’аламбер помітив, що «математика щедра, вона часто дає більше, ніж у неї просять». Сьогодні у нас урок – ділова гра «Компетентність». Під час уроку ми узагальнимо знання, вміння та навички розв’язання квадратних рівнянь; будемо розвивати пізнавальну, особистісну, самоосвітню,соціальну, творчу компетентності. Чи є у вас на початку уроку до мене запитання? (Очікуване запитання. Що таке компетентність?).

Психологи визначають компетентність як добру обізнаність людини із чим-небудь. Компетентний учень – такий, який має знання, володіє вміннями, вміє застосувати набуті знання та досвід. Компетентний спеціаліст, компетентна людина − це гідна перспектива.

Отже, наша мета – перевірити, наскільки ви компетентно розв’язуєте квадратні рівняння. Успіхів вам.

III . Актуалізація опорних знань.

Перший етап «Теорія – основа практики»

Мета – повторити опорні факти теоретичного матеріалу.

Завдання: для виявлення учня, який краще за решту готовий до роботи в сучасних умовах, пропоную відгадати математичний кросворд, запитання в якому пов’язані з нашою темою.

Слайд 1. Кросворд «Квадратні рівняння».

1.
		2.
	3.
			5.
	6.

1.               Рівність зі змінною.
2.               Співвідношення величин, записане рівністю.
3.               Другий степінь числа.
4.               Числовий множник алгебраїчного виразу.
5.               Розв’язок рівняння.
6.               Графік квадратного рівняння.

Відповіді : 1. Рівняння. 2. Формула. 3.Квадрат. 4.Коефіцієнт. 5. Корінь. 6.Парабола.

Учні перевіряють відповіді. Кожна правильна відповідь оцінюється 0,5 бала.

Слайд 2. Пригадаємо:

• Які рівняння називаються квадратними?
• На які види поділяються квадратні рівняння?
• Прокоментуйте види рівнянь:

А) х²- 29=0; Б) 2х² – 5х – 10=0; В) х²-17х+27=0; Г)-х²+3х+4=0; Д)х²-3х=0.

• Скільки дійсних коренів може мати квадратне рівняння?
• Від чого це залежить?
• Вставте  пропущене:

D>0,    D=…-4ac,    х₁=,     х₂=.

D=0,   х=.

D<…,  коренів немає

(Кожна правильна відповідь 0,5 бала)

Підбиття підсумків першого етапу.

Задоволена вашими теоретичними знаннями, впевнена, що ви успішно застосуєте їх у подальшій роботі.

IV. Застосування знань, умінь і навичок у стандартних ситуаціях.

Мета – перевірити вміння учнів розв’язувати квадратні рівняння за  формулою.

Звертаю вашу увагу на пам’ятку щодо розв’язання квадратного рівняння за формулою, у якій ви знайдете потрібний вам алгоритм.

1.               Найпростіша відтворювальна самостійна робота (за зразком). Учні розв’язують рівняння під номером 1 та 2 (по варіантах) (див. табл. 1).

1)3х²-13х+4 =0,                                               2) 2х²-5х +2=0,

D=b²-4ac=(-13)²-4×3×4=121>0,                   D=b²-4ac=(-5)²-4×2×2=9>0,

==11,                                                  ==3,     

 х₁===4,                                        x₁===

 x₂===.                                         x₂===2.

Відповідь:{4; }.                                             Відповідь:{2; }.

 

Перевірка з дошки, за правильне розв’язання завдання 1 бал.

 

На цьому етапі ми з’ясували чи готові ви робити в малих групах, тобто чи вмієте ви співпрацювати.

 

 

 

 

 

 

Таблиця 1.

Найпростіша відтворювальна самостійна робота ( за зразком)

Розв’язування квадратних рівнянь за формулою коренів

Алгоритм	Приклад	Розв’яжи сам	Розв’яжіть рівняння за зразком: 1) 3х2 – 5х +4 = 0; 2) 2х2 – 5х + 2 = 0; 3) 5х2 – 13х + 6 = 0; 4) 9х2 – 12х + 4 = 0; 5) 49х2 – 28х + 3 = 0; 6) 18х2 – 9х – 5 = 0; 7)  – х2  - 8х + 12 = 0; 8) 5х2 + 8х + 3 = 0; 9) х2 – 10х – 24 = 0; 10) х2 + 3х – 4 = 0; 11) х2 – 3х + 28 = 0; 12) х2 + х + 8 = 0.
ax2 + bx + c = 0 1. Визначимо коефіцієнти: a = ____,  b = ____,  c = ____   2. Обчислимо дискримінант за формулою D = b2 – 4ac = ____________   3. Порівняємо D із нулем.   4. 1) ЯкщоD0, то обчислимо = ____________ та знайдемо його корені: x1 = = ____________; x2 = = ____________; Відповідь. x1, x2.   2) ЯкщоD = 0, то знайдемо корінь:x = . Відповідь. x.   3) ЯкщоD 0, то коренів немає. Відповідь.Коренів немає	x2 – 4x + 3 = 0 a = 1 b = -4 c = 3. D = (-4)2 – 4·1·3 = 4>0 х1=(4-2)/2=1; x2=(4+2)/2=3. Відповідь:{1:3}.	x2 + 5x +4 = 0

 

2.               Виконаємо реконструктивно–варіативну самостійну роботу. Інтерактивна вправа «Робота в парах».

Розв’яжіть рівняння, попередньо записавши їх устандартному вигляді:

1)х²+5х=14,   2)3х²=2х+5,   3)(4х-3)²+(3х-1)(3х+1)=9,   4)25х²+10=10х+9,

х²+5х-14=0,      3х²-2х-5=0,      16x²-24x+9+9x²-1-9=0,       25x²+10-10x-9=0,

D=25+56=81,    D=4+60=64,        25х²-24х-1=0,                   25х²-10х-9=0,

х₁==2,          х₁==,                  D=676,                               D=0,

х₂==-7.           х₂==-1.            х₁==1,                         x=-,

                                                               x₂==-            x=.

Відповідь:{2;-7}   Відповідь:{;-1}   Відповідь:{1;-}            Відповідь:{}

За правильно розв’язане рівняння учні отримують 2 бали.

Що показав третій етап? Чи готові ви показати свої уміння далі?

V. Застосування знань у змінених умовах.

Третій етап «Від практики до творчості»

Мета – перевірити вміння учнів застосовувати набуті знання.

Зараз ми будемо працювати командою. Пам’ятайте, що робота кожного члена команди приносить користь усій команді.

Завдання 1. Знайдіть корінь рівняння Iх²+х-3I=х.

Розв’язання: х²+х-3=х                           або           х²+х-3=-х,

                         х²-3=0,                                               х²+2х-3=0,

                      (х-)(х+)=0,                             D=4 +12=16>0,

              х-=0 або х+=0,                          х₁==1, х₂==-3.

              х₁=,           х₂=-.

Враховуючи, що Iх²+х-3I>0,  х>0 маємо відповідь та 1.

Завдання 2. При яких значеннях параметра а має один корінь рівняння

ах²-6х -7=0?

Розв’язання:  D=b²-4ac=36+28a,

                         D=0,

                         36+28a=0,

                            a=-,      a=-.

Відповідь: при а=- дане рівняння має один корінь.

Найбільш активні учні отримують бонус – 1т бал.

Цей етап закінчено. Чи ми вміємо працювати у команді?

VI.Підбиття підсумків уроку.

Підіб’ємо підсумок уроку за допомогою двох дієслів – «знаю» та «умію». (Відповіді учнів).Учні роблять самоаналіз за картками самоконтролю.

Учитель. Що дала нам сьогодні алгебра крім вмінь розв’язувати квадратні рівняння? (Очікувані відповіді. Працювати самостійно,співпрацювати, робити самооцінку своїх можливостей, творчо мислити,вирішувати проблеми). Чи можете ви назвати себе компетентними  в розв’язанні квадратних рівнянь?

Наш урок підтвердив, що ви вмієте застосовувати набуті знання, а це означає, що кожен із вас як і сьогодні, так і в майбутньому буде компетентний у певній галузі. Дякую за співпрацю на уроці.

VII. Домашнє завдання.

Домашнє завдання учні отримують на картках, виконують вибірково.

Обов’язків рівень.

.

.

Достатній рівень.

.

.

Високий рівень.

.

 

Картка самоконтролю

Прізвище, ім’я учня
Кросворд (0,5 балів за 1 правильну відповідь)	Пригадаємо (0,5 балів за одну правильну відповідь)	Рівняння за зразком (1 бал)	Робота в парах (2 бала)	Завдання 1 (2 бали)	Завдання 2 (2 бали)