Заняття № 9-10 на тему: «Найпростіші Діофантові рівняння» для 7 класу

Заняття № 9-10 на тему: «Найпростіші Діофантові рівняння» до програми факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики».

Дане заняття відповідає діючій програмі факультативного курсу з математики для 7 класу Бевз В. Г, Бурда М. І., Прокопенко Н. С. «За лаштунками шкільної математики». Воно містить теоретичний матеріал, що відображає тему, приклади завдань з розв’язками та вправи для самостійного виконання.

Враховуючи інтереси та нахили учнів, їхню підготовленість, вчитель може доповнювати зміст заняття додатковим матеріалом, змінювати та удосконалювати методику проведення.

Тема 1. Подільність і прості числа

Заняття 9-10

Найпростіші Діофантові рівняння

Одним із своєрідних давньогрецьких математиків був Діофант Олександрійський, праці якого мали велике значення для алгебри і теорії чисел. Жив і творив Діофант у ІІІ столітті нашої ери. Він прожив 84 роки.

З праць Діофанта найважливішою є «Арифметика», з 13 книг якої  до наших днів збереглося лише 6. В книгах Діофанта збереглися 189 рівнянь  з розв’язками. Одна книга містить  визначені рівняння першого  та другого степеня, а всі інші книги – невизначені рівняння. Методи розв'язування невизначених рівнянь складають основний вклад Діофанта в математику. Відомо, що в символіці Діофанта  був лише один знак для невідомого. Діофант позначав невідоме , а поняття «дорівнює» буквою (від грецького слова «ізосис» - «рівність»). Розв’язуючи невизначені рівняння, він застосовував в якості декількох невідомих довільні числа, замість яких можна було взяти будь-які інші, що зберігало характер його розв’язку.

В Індії та в Китаї невизначені рівняння розв’язувалися в зв’язку з астрономічними запитами і календарними розрахунками, ставилося питання про знаходження цілочисельних розв’язків невизначених рівнянь. Перші натяки на загальний розв’язок діофантових рівнянь виду ах+ву=с, зустрічаються в працях індійського астронома Ариабхатти. Детальні розв’язки виклали індійські математики Брахмагупта і Бхаскара. Загальний метод для розв'язування в цілих числах діофантових рівнянь першого степеня з цілими коефіцієнтами було названо в Індії методом розсіювання.

Праці Діофанта стали відправною точкою для розвитку теорії чисел Ферма, Ейлером і Гауссом.

Діафантовими називають алгебраїчні рівняння з цілими коефіцієнтами, для яких треба знайти цілі розв’язки. При цьому кількість невідомих перевищує кількість рівнянь. Як правило, діофантові рівняння містять більше однієї невідомої величини, мають багато розв’язків, у зв’язку з чим їх ще називають невизначеними рівняннями.

Наприклад: 3х+5у=7, , .

Відоме рівняння Ферма, яке більше трьохсот років тому він написав на полях «Арифметики» Діофанта , нещодавно розв’язано.

Розв'язування рівнянь у цілих числах – один із найкрасивіших розділів математики.

До діофантових рівнянь приводять задачі, за змістом яких невідомі значення величин можуть бути тільки цілими числами.

Задача

•             Покупець, який мав купюри лише по 5 грн. і 2 грн., купив у магазині товар на 43 грн. Покупець стверджував, що 43 грн.  не можна сплатити по 2 грн. і по 5 грн. Чи правий він? Якщо ні, то яка найменша кількість купюр потрібна?

Розв'язання.

Нехай буде потрібно х купюр по 2грн. та у купюр по 5грн. Зрозуміло, що х та у - натуральні числа. Тоді одержимо рівняння:

2х+5у = 43,

2х = 43-5у.

Якщо розв’язок існує, то 43-5у повинно ділитися на 2. Підходить у=1. Тоді

,

Взагалі для будь-якого непарного у, де знайдеться відповідне значення х. Отже, розв’язками будуть пари чисел: (19;1), (14;3), (9;5), (4;7).

Відповідь: можна заплатити чотирма способами, найменша кількість купюр 11.

Аналіз результатів задачі.

х=19,  у=1 - один із розв’язків рівняння 2х+5у=43. Наступні значення х знаходимо відніманням 5, а значення у – додаванням 2.

Висловлюємо гіпотезу про те, що всі цілі розв’язки цього рівняння можна задати формулами:

y=1+2t, x=19-5t, де .

Теорема

Hехай і – взаємно-прості числа і ( - довільний розв’язок рівняння ах+ву+с=0. Тоді формули , , де , дають усі розв’язки даного рівняння.

Доведення.

Нехай (х;у) – довільний розв’язок  рівняння ах+ву+с=0.

Тоді з рівностей

ах + ву + с=0,

ах₀ + ву₀ + с=0

одержуємо

ах - ах₀ + ву - ву₀ = 0,

.

Оскільки  (у-у₀) -  ціле число, а числа а   і   в – взаємно прості, то  (х-х₀)  повинно ділитися націло на в, тобто (х-х₀)  має вигляд:

(х-х₀)=bt, .

х = х₀ - вt.

Але тоді

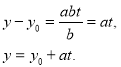
•             Для перевезення 289 учасників олімпіади виділено автобуси місткістю по 11 і 16 місць. Скількома способами можна розсадити учасників так, щоб усі місця були зайняті? Яка найменша кількість автобусів потрібна?

Розв'язання.

Нехай потрібно х автобусів по 11 місць та у автобусів по 16 місць.

Тоді

11х+16у=289,

Якщо у=5, то маємо:

Тобто (19;5) – один із розв’язків.

Усі цілочислові розв’язки мають вигляд:

x=19-16t,

y=5+11t, .

Оскільки нас цікавлять натуральні розв’язки, то

t=0, x₁=19, y₁=5;

t=1, x₂=3, y₂=16;

Відповідь:  (19;5), (3;16) ; найменша кількість автобусів 19.

У множині раціональних чисел рівняння ах+ву=с, де а,в,с - цілі числа, має безліч розв’язків. Надамо одній із змінних, наприклад х, конкретного значення і знаходимо відповідне значення змінної у.

Коли с не ділиться на спільний дільник чисел а та в, то таке рівняння не має розв’язків у цілих числах. Якщо а та в взаємно прості, то існує нескінченна множина розв’язків: х=х₀+вt, у=у₀+аt, де (х_0;у₀) – який-небудь один із розв’язків, tZ. Покажемо це. Дійсно, якщо (х_0;у₀)  розв’язок, то ах₀+ву₀=с.Віднімаючи цю рівність від початкового рівняння, дістанемо

а(х-х₀)+в(у-у₀)=0, звідки . З умови того, що число х ціле число другий доданок останньої рівності повинен бути теж цілим, а враховуючи те, що а та в взаємно прості, вираз (у₀ -у) має ділитися на а. Отже,  у₀ - у= аt, 

Як же знайти той один розв’язок  (х_0;у₀)?  

•             Розв’язати в цілих числах рівняння 19х+97у=1997.

Розв'язання.

Виразимо змінну х через у.

Маємо

Оскільки число х має бути цілим, то це буде лише при у₀=1. Тоді х₀=100. Тому всі розв’язки даного рівняння можна задати формулами

х=100+97п і у=1-19п, де

Використана література

1. Адлер А. Теорія геометричних побудов, Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
2. Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
3. Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
4. Воронець О. М. Геометрія циркуля, Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
5. Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с.
6. Манін Ю. І., Про розв'язність задач на побудову за допомогою циркуля та лінійки, Енциклопедія елементарної математики книга четверта (геометрія), М., Фізматвид, 1963. — 568с.
7. Петерсен Ю. Методи і теорії розв'язку геометричних задач на побудову, Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
8. Прасолов В. В.. Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура кола. М.: Наука, 1992. 80 с. Серія <Популярні лекції з математики>, випуск 62.
9. Щетников А. І. Як було знайдено де-які розв'язки трьох класичних задач древності? Математична освіта, № 4 (48), 2008, с. 3-15.
10. Слива Н. В.Математика 7клас. Факультативний курс http://www.fak-matematika_7_klas_sliva_n.v.