Розробка уроку "ЦИРКУЛЬНІ КРИВІ"

ВИКОНАВЧИЙ ОРГАН КИЇВСЬКОЇ МІСЬКОЇ РАДИ

(КИЇВСЬКА МІСЬКА ДЕРЖАВНА АДМІНІСТРАЦІЯ) ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ

 

 

 

КИЇВСЬКЕ ВИЩЕ ПРОФЕСІЙНЕ УЧИЛИЩЕ 

БУДІВНИЦТВА І ДИЗАЙНУ

 

 

 

 

 

 

 

МЕТОДИЧНА РОЗРОБКА УРОКУ

 з предмету «Креслення» на тему:

 

“ПЛОСКІ КРИВІ ЛІНІЇ. ЦИРКУЛЬНІ ПРЯМІ”

 

 

 

 

 

 

 

 

 

Підготувала: викладачка

вищої категорії

Малець Наталія

 

 

 

 

 

 

 

 

Київ-2023 р.

Тема уроку: ПЛОСКІ КРИВІ ЛІНІЇ. ЦИРКУЛЬНІ КРИВІ Мета уроку: Навчальна –

•                ознайомити здобувачів освіти із циркульними кривими,

•                навчити будувати циркульні криві різної складності, Розвивальна –

•                розвивати творче мислення та просторову уяву, логічне мислення здобувачів освіти,

•                розвивати пізнавальний інтерес до предметів професійної підготовки та уроків креслення,

•                розвивати комунікабельність, уміння вирішувати поставлені завдання.

Виховна –

•                виховувати у здобувачів освіти усвідомлення важливості якості роботи при виконанні креслення,

•                виховувати креативність, акуратність, наполегливість,

•                виховувати риси сучасного фахівця, підвищувати інтерес та виховувати любов до обраної професії.

Тип уроку : урок засвоєння нових знань, навичок і умінь Метод проведення:

•                Пояснювально-ілюстрований (пояснення, розповідь з елементами бесіди та використанням мультимедійної презентації, робота з опорними конспектами)

•                Досліджувальний (практична робота та виконання креслення).

•                Тестові завдання, мозковий штурм, фронтальне опитування.

Міжпредметні зв’язки : 

•                Геометрія

•                Уроки технологій

•                Уроки виробничого навчання

•                Спецтехнологія 

•                Читання креслень

Матеріально-технічне забезпечення уроку:

•                Мультимедійний проєктор, презентація до уроку.

•                Опорний конспект, тестові завдання.

•                Креслярські інструменти, креслярський папір, підручники . 

Літературні джерела: 

1)  ДСТУ 3321:2003. Система конструкторської документації. – К.: Держспоживстандарт України, 2005

2)  Технічне креслення та комп’ютерна графіка: навч. посібник / П.П.

Волошкевич, О.О. Бойко, П.А. Базишин, Н.О. Мацура. - Львів: Світ, 2014. - 224 с. 

3)  Антонович Є.А., Василишин Я.В., Шпільчак В.А. А 72 Креслення: Навч. посібник/ За ред. проф. Є.А. Антоновича. — Львів: Світ, 2006. — 512 с, іл.

4)  Сидоренко В. К. Креслення / В. К. Сидоренко. – Львів: Оріяна-Нова, 2004. – 356 с.

5)  Основи архітектурної графіки : навч. посібник / А. О. Радченко, О. Ю. Усачова; Харків. нац. ун-т міськ. госп-ва ім. О. М. Бекетова. – Харків: ХНУМГ ім. О. М. Бекетова, 2018. – 248 c.

6)  Антонюк С. М. Світ креслення. Педагогічний програмний засіб

[Електронний ресурс] / С. М. Антонюк. – 2018. – Режим доступу до ресурсу: http://kreslennja.com.ua.

7)  Основи креслення [Електронний ресурс]. – 2010. – Режим доступу до ресурсу: http://kreslennya.com/.

 

СТРУКТУРА УРОКУ:

1.     Організаційна частина – 2 хв.

2.     Актуалізація знань - 10 хв.

3.     Мотивація навчальної діяльності – 1 хв.

4.     Засвоєння нових знань, формування вмінь і навичок – 27 хв.

5.     Підведення підсумків – 3 хв.

6.     Інструктаж домашнього завдання – 2 хв.

ХІД УРОКУ:

1.          Організаційний момент.

Привітання зі здобувачами освіти, перевірка присутності на уроці, організація робочого місця, оголошення теми і мети уроку.

Коротко назвати основні вимого щодо роботи на уроці, види робіт, які будуть запропоновані учням, обладнання для результативного виконання завдання, нагадати здобувачам освіти інструктаж з БЖД при роботі з креслярськими інструментами (всіма креслярськими приладдями, якими користуються здобувачі освіти під час уроку – не гратися, використовувати їх лише за призначенням та вказівками викладача, інструменти з гострими кінцями (циркуль, олівець) тримати в закритих футлярах). 

 

2.          Актуалізація знань.

Перевірка знань здобувачів освіти за попередніми темами. На уроці застосовані дидактично-ігрові методи перевірки знань, в яких освітня, розвиваюча й виховна функція діють у тісному взаємозв’язку. 

2.1. Дайте правильні відповідь на тестові питання.

1.       Яке позначення згідно ДСТУ у  має креслярський формат розміром 210×297? а) А0;      

б) А1;          

в) А3;        

г) А4;      

2.       З якої сторони формату залишають поле 20мм для підшивання креслень? а) внизу формату;            

б) з правої сторони;

в) з лівої сторони;             

г) зверху формату.

3.       Якою лінією на кресленні  позначають невидимий контур деталі?

а) суцільною товстою основною;   

б) суцільною хвилястою;   

в) штрихпунктирною  тонкою;   

г) штриховою.

4.       Яким номером позначено лінію видимого контуру?

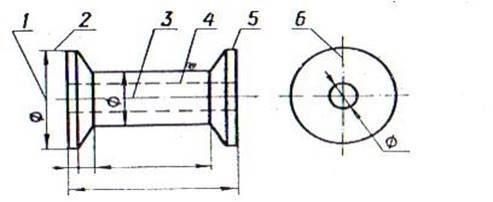                          а) 2;

б) 5;

в) 6;

г) 1.

5.       В якому куті поля креслення розміщують основний напис?   

а) в правому верхньому куті;     

б) в правому нижньому куті;   

в) в лівому нижньому куті;      

г) в лівому верхньому куті.

6.       Якою лінією на кресленні позначають осі та центри деталей?

а) суцільною тонкою;

б) штрихпукнктирною  тонкою;

в) штриховою;

г) штрихпунктирною  з двома крапками;

7.       Яким номером позначено осьову лінію?

               

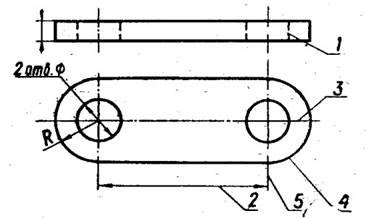
а) 3;

б) 4;

в) 2;

г) 1.

8.       Яку довжину деталі необхідно поставити на кресленні, якщо вона дорівнює 350мм, а креслення виконано в масштабі М1:5?

а) 350;     

б) 175мм;      

в) 87,5;      

г) 70мм;      

9.       Який знак чи букву необхідно поставити перед розмірним числом що показує діаметр кола?

а) D;        

б) Ø;        

в) R;      

г) L;        

10.   Чому дорівнює висота малих літер шрифту розміру 10?

а) 3,5мм;

б) 5мм;

в) 7мм;

г) 10мм;

11.   Чому дорівнює висота малих літер, що мають виступаючі елементи б,д,р,ф?

а) висоті великих літер;

б) висоті малих літер;

в) більше висоти великих літер;

г) ширині великих літер;

12.   Як називається масштаб М1:1?

а) масштаб збільшення;

б) масштаб натуральної величини;

в) .масштаб зменшення

г) масштаб розміру;

13.   При якому масштабі зображення деталі буде найменшим?

а) М1:1;

б) М2:1;

в) М1:4;

г) М1:5;

14.   Визначте, на яких кресленнях нанесено розміри з помилками?

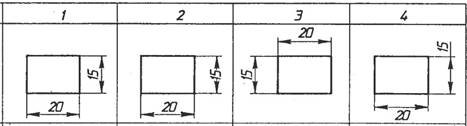 а) 1;

б) 2;

в) 3;

г) 4;

15.   Які габаритні розміри має запропонована деталь?

 

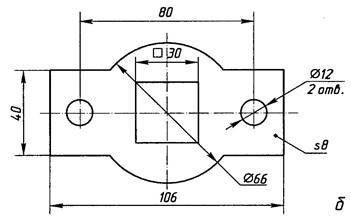
а) 106×40×8

б) 106×80×12;

в) 80×30×40;

г) 106×66×8.

16.   Як називається точка плавного переходу однієї  лінії до іншої?

а) спряженням;

б) плавним переходом;

в) точка спряження;

г) центом спряження;

17.   Чому дорівнює радіус спряження паралельних прямих відстань між якими дорівнює 48мм?

а) 12мм;

б) 24мм;

в) 36мм;

г) 48мм;

 

2.2. Дайте правильні відповіді на запитання кросворду, щоб визначити ключове слово (Креслярський інструмент для проведення кіл та дуг):

 

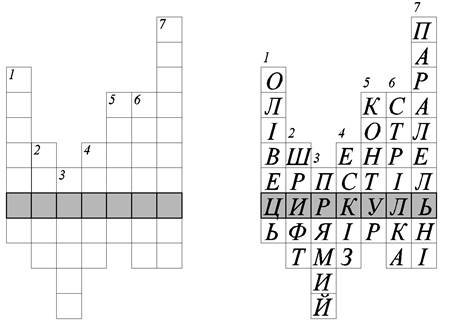
Рис.1. Кросворд

 

1.     Інструмент, яким виконують креслення (олівець)

2.     Написи літер і цифр на кресленні (шрифт)

3.     Кут, який утворюють перпендикулярні прямі (прямий)

4.     Креслення виконане від руки без додержання масштабу (ескіз)

5.     Видимі обриси деталі (контур)

6.     Закінчення розмірної лінії (стрілка)

7.     Лінії, які не перетинаються (паралельні). 

Отже, ми отримати слово «Циркуль». 

 

Циркуль – креслярський предмет, відомий кожному зі шкільних років. Основним його призначенням є креслення дуг та кіл, вимірювання відстаней тощо. Циркуль широко використовують у геометрії, кресленні, навігації, медицині та у ряді інших. Але цікаво трохи більше дізнатись про цей на перший погляд звичайний предмет.

Історія винайдення циркуля

Слово «циркуль» походить від латинського circus, що означає коло, кільце, обруч. Своє теперішнє звучання воно отримало завдяки польському варіанту cyrkuɫ або німецькому Zirkel. Достеменно невідомо хто саме винайшов циркуль, однак існує легенда у Древньогрецьких міфах.

У древні часи в Афінах жив молодий винахідник Талос, племінник відомого Дедала. Уже в 12 років він придумав гончарний круг, за допомогою якого можна було виготовляти різний посуд. Гуляючи по берегу моря, Талос підняв скелет риби, і це наштовхнуло його на ідею іншого винаходу - пили. Поєднавши шарніром дві однакові палички, Талос придумав циркуль. Дедал позаздрив генію свого племінника і одного разу на прогулянці зіштовхнув Талоса з міського валу.

Лінійка    та      циркуль      вважаються          найдавнішими креслярськими інструментами. Знахідки часів древньої Вавілонії  та Ассирії – вирізьблені чаши, кубки, настінні малюнки – вказують на наявність циркуля та лінійки у майстрів тих часів. Оскільки неможливо уявити як без цих інструментів можна вирізати настільки ідеальне коло чи лінію.

Найдавніший залізний циркуль було знайдено на території сучасної Франції під час розкопок кургану. Велика кількість бронзових циркулів більш ніж дві тисячі років провела у попелі, що 1900 років тому поховав древнє місто Помпеї.

Цікавий аналог циркуля - друлівник - використовували на Гуцульщині. Цей інструмент використовувався для викреслювання кіл на металі.

Сучасний циркуль

За давніх часів конструкція циркуля майже не змінилася. Проте для нього винайшли велику кількість насадок, що дозволяють викреслювати кола діаметром від 2 мм до 60 см. Окрім цього звичайний графітний грифель можна замінити насадкою з рейсфедером для роботи з тушшю.

Сучасний циркуль можна поділити на наступні основні види:

•            Креслярський циркуль – це класичний вид циркуля, відомий ще зі шкільних років.

•            Кронциркуль використовується для вимірювання ширини отворів, коли неможливо зробити це за допомогою лінійки. Кронциркуль буває для внутрішніх та зовнішніх вимірювань.

•            Пропорційний циркуль дозволяю зменшити чи збільшити довжину відрізка у потрібну кількість раз.

•            Штангенциркуль використовують для точних вимірювань розмірів предметів та глибин отворів.

•            Козяча ніжка – вид циркуля, де замість грифеля використовують звичайний олівець.

 

 

 

3.     Мотивація навчальної діяльності.

Отже, циркуль – це креслярський інструмент для проведення кіл та дуг

Сьогодні на уроці ми ознайомимося з плоскими кривими лініями і навчимося їх застосовувати на практиці. Тема сьогоднішнього уроку: «Плоскі криві лінії.

Циркульні криві».

4.     Засвоєння нових знань, формування вмінь і навичок

Криві, у яких усі точки розташовані в одній площині, називають плоскими. Частина плоских кривих, що складаються з дуг кіл, утворює групу циркульних кривих. Дуги циркульних кривих торкаються одна одної, тому їх побудова ґрунтується на правилах спряження та виконується за допомогою циркуля.

Інша частина плоских кривих, які не можна побудувати за допомогою циркуля, належить до групи лекальних кривих. Лекальні криві будують за точками, знаючи закон їх утворення, а обводять за лекалом.

 

Циркульні криві

•            Завитки

Спіральна крива, накреслена циркулем шляхом спряження дуг кіл різних радіусів, називається завитком. На рисунку 2 зображено побудову двоцентрового завитка. 

 

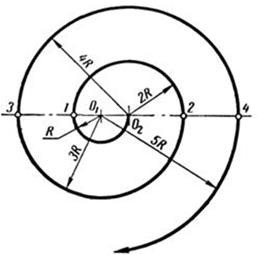
Рис.2. Двоцентричний завиток

 

Він складається з ряду півкіл, описаних поперемінно із заданих центрів О₁ і О₂. Точки дотику проведених дуг розташовані на прямій, що з’єднує ці центри. Перше півколо описують радіусом Я, що дорівнює відстані між центрами 0₁ і 02. Радіус кожного наступного півкола збільшують на величину початкового радіуса R. Отже, друге півколо описують радіусом 2R, третє — радіусом 3R тощо.

Побудову трицентрового завитка за заданими центрами Оі, 02 і 0₃, розташованими у вершинах рівностороннього трикутника, наведено на рисунку 3. 

 

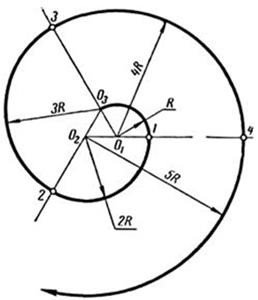
Рис.3. Трицентричний завиток

 

Через кожну пару центрів проводять пряму лінію. З центра 0₁ описують дугу радіусом R = 0₁0₃ у межах між точками 0₃ і 1. Наступну дугу радіусом 2R проводять із центра 0₂ до точки 2. Потім описують дугу радіусом 3R із центра 0₃. Дуга, проведена знову з центра 0₁, має радіус 4R тощо. Завитки чотирьохцентрові, п’ятицентрові тощо будують так само.

 

• Коробові криві

Коробовою кривою називається односторонньо опукла циркульна крива (замкнена або незамкнена), утворена спряженням дуг кіл. Існує декілька різновидів коробових кривих.

Овал — замкнена коробова крива, що має дві осі симетрії. Елементами, що визначають розмір овала, є його довжина і ширина, які вимірюються за осями симетрії.

Побудову овала за його довжиною АВ і шириною СD наведено на рисунку 4. 

 

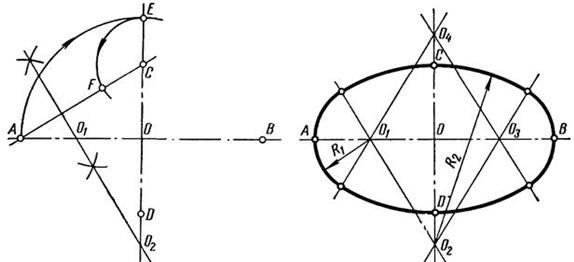
Рис.4. Побудова овала

1.        Проводимо дві взаємно перпендикулярні прямі, що перетинаються в точці О

(рис. 4, а). 

2.        На горизонтальній прямій в обидві сторони від точки О відкладають відрізок АВ/2, а на вертикальній — СD/2.  

3.        Точки А і С З’єднують прямою лінією.  

4.        З точки О описують дугу радіусом ОА до перетину її з прямою СD у точці Е.

5.        На прямій АС відкладають відрізок СF = СЕ і отримують точку F.  

6.        Через середину відрізка АF проводимо перпендикуляр і на перетині його з прямими АВ і СD отримують точки О₁ і О₂.  

7.        На прямих АВ і СD будують точки О₃ і О₄, симетричні точкам О₁ і О₂ щодо центра О (рис. 4, б). Точки О₁, О₂, О₃, О₄ є центрами сполучених дуг, що визначають контур овала, а точки дотику дуг розташовуються на прямих О₁О₂, О3О2, О1О4 і О3О4.  

8.        З центрів О₁ і О₃ описують дуги радіусом R₁ = О₁А, а з центрів О₂ і О₄ — дуги радіусом R₂ = О₂С і отримують контур овала.

 

В архітектурі (рис. 5-7) овальні форми мають арки споруд, зокрема стилю бароко. Одна з принципових відмінностей ренесансу від бароко полягає в тому, що перший стиль використовує коло, а другий — овал або еліпс.

 

Рисунок 5. Арка Мосту Зітхань у Венеції (близько 1600 р.)

 

Рис. 6. Купол церкви Сан Карло біля чотирьох фонтанів у Римі (початок будівництва — 1634 р.)

 

Рисунок 7. Вілла д’Есте. Овальний фонтан. 1567, архітектор Пірро Лігоріо

 

Овоїд — замкнена коробова крива, що має одну вісь симетрії. Побудову овоїда за його шириною — відрізком АВ — наведено на рисунку 8. 

  

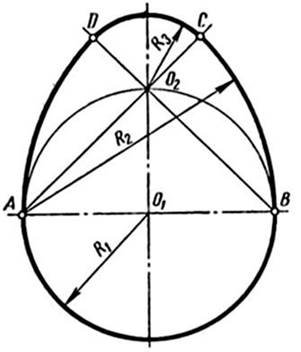
Рисунок 8. Овоїди

 

1.     Через середину відрізка АВ — точку О₁ — проводять пряму, перпендикулярну до нього. 

2.     З точки О₁ описують коло радіусом R1 = АВ/2 і на перетині його з перпендикуляром отримують точку О₂. 

3.     Проводимо прямі АО₂ і ВО₂ і продовжують їх за точку О₂. 

4.     З точок А і В радіусом R₂ = АВ описують дві дуги до їх перетину у точках С і D із проведеними прямими.  5.Останню дугу радіусом R₃ = О₂С описують із точки О₂.

 

Коробові криві зводів — криві, що належать до незамкнених коробових кривих. Вони застосовуються у будівництві зводів і арок мостів, входів до будинків, різних перекриттів, наприклад метро тощо. Нижче розібрано побудову коробових кривих пологого, крутого й повзучого зводів.

1.   Побудова коробової кривої пологого зводу за шириною АВ і висотою ОС.

 

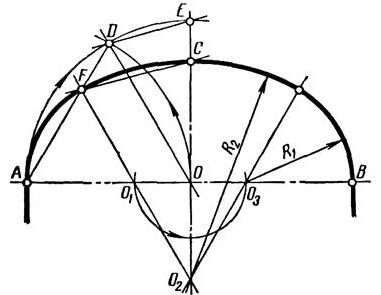
Рисунок 9. Побудова коробової кривої пологого зводу

1.     На горизонтальній прямій (рис. 9) відкладають ширину зводу — відрізок АВ і через його середину — точку О проводять пряму, перпендикулярну до нього. 

2.     На цій прямій від точки О відкладають висоту зводу — відрізок ОС.

3.     З точки О радіусом ОА описують дугу АЕ і на ній відзначають точку D за допомогою того самого радіуса ОA, але з центром у точці А. 

4.     Точку D з’єднують прямими з точками А, Е і О. 

5.     Через точку С проводять пряму СF || DE до перетину її з прямою AD у точці

F. 

6.     Через точку F проводять пряму FО₂ || DО до перетину її з відрізком AВ у точці О₁, а з прямою ОС у точці О₂. 

7.     Точку О₃ отримуємо за допомогою дуги радіуса ОО₁. Отримані точки О₁, О₂ і О₃ є центрами дуг, з яких складається ця крива. 

8.     Радіусом R₁ = О₃В описують дуги з центрів О₁ і О₃, а радіусом R₂ = О₂С — дугу з центра О₂.

 

На рисунку 10 наведено приклад застосування пологого зводу.

 

Рисунок 10. Станція метро «Золоті ворота» в Києві

 

2.   Побудова коробової кривої крутого зводу за його шириною AB і висотою ОС

 

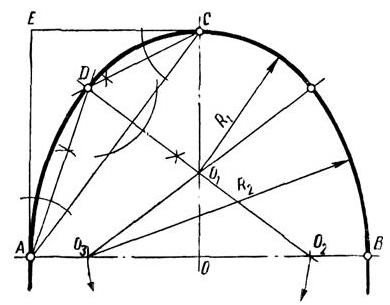
Рисунок 11. Побудова коробової кривої крутого зводу

1.   Відрізок АВ (рис. 11) ділять навпіл, будують прямокутник АЕСО і проводять у ньому діагональ АС. 

2.   Кути ЕАС і ЕСА ділять навпіл. 

3.   На перетині бісектрис цих кутів отримують точку D, з якої опускають перпендикуляр на діагональ АС. 

4.   Перпендикуляр продовжують до перетину з відрізками ОС у точці O₁ і АВ у т. O₂.  5. Точку O₃ отримують за допомогою дуги радіуса OO₂. Точки O₁, O₂ і O₃ є центрами дуг радіусів R₁ і R₂, за допомогою яких будують контур кривої.

В архітектурі круті зводи найчастіше використовувалися у будівництві соборів. Вони відрізняються великою різноманітністю форм. Один з таких зводів наведено на рисунку 12.

 

Рисунок 12. Собор Святих Ольги та Єлизавети у Львові

 

3. Побудова коробової кривої повзучого зводу за його шириною АВ і прямою CD, дотичною до вершини зводу

 

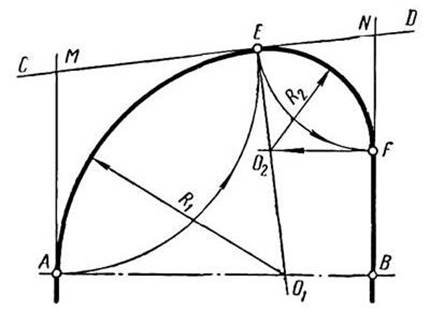
Рисунок 13. Побудова коробової кривої повзучого зводу

1.     Будуємо відрізок АВ (рис. 13), що становить ширину зводу, і пряму СD (її називають замковою прямою).  

2.     З точок А і В проводять до відрізка АВ перпендикуляри і продовжують їх до перетину з прямою СD у точках М і N.  

3.     На прямій СD відкладають відрізок ЕМ = АМ.  

4.     З отриманої точки Е — вершини зводу — проводять перпендикуляр до прямої СD і на перетині його з відрізком АВ відзначають точку О₁.  

5.     На прямій BN відкладають від точки N відрізок FN = ЕN  

6.     З точки F проводять пряму, паралельну відрізку АВ, до перетину з прямою ЕО₁ у точці О₂. У точках О₁ і О₂ знаходяться центри дуг R₁ = О₁А і R₂ = О₂F, що визначають контур повзучого зводу.

Повзучі зводи застосовуються у оформленні арок входів, розташованих на похилих площинах, наприклад на сходах. Один із таких прикладів наведено на рисунку 14.

 

Рисунок 14. Успенська церква

 

6. Інструктаж домашнього завдання

Здобувачам освіти пропонуються виконати графічну роботу. 

1. За наочним зображенням  (рис. 2,3,4,8,9,11,13) виконати циркульні криві з наступними розмірами:

1.1. Двоцентричний завиток, R=30 мм

1.2.Трицентричний завиток, R=40 мм

1.3. Овал, АВ=120 мм; CD=80 мм

1.4. Овоїд, АВ=80 мм

1.5. Пологий звод, АВ=90 мм; ОС=48мм

1.6. Крутий звод, АВ=84 мм; ОС=76мм

1.7. Повзучий звод, АВ=90 мм

 

2. § 5.3 закріпити знання, дати відповіді на питання (ст. 41) [3]

 

Заключне слово викладача.