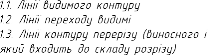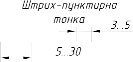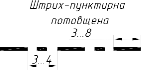Нарисна геометрiя та iнженерна графiка
Міністерство освіти і науки України
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
«ОДЕСЬКА МОРСЬКА АКАДЕМІЯ»
М.В. КОРХ
НАРИСНА ГЕОМЕТРІЯ
ТА ІНЖЕНЕРНА ГРАФІКА
Частина І
НАВЧАЛЬНИЙ ПОСІБНИК
Одеса – 2017
УДК 744:004.92
К 70
Рекомендовано до друку рішенням Вченої ради НУ «ОМА» як навчальний посібник з дисципліни «Нарисна геометрія та інженерна графіка» Частина І, протокол №___від ___._________.2017.
Рецензенти: В.М. Харін, завідувач кафедри судових допоміжних механізмів Національного університету «Одеська морська академія», доктор технічних наук, професор;
А.В. Конопльов, завідувач кафедри ТММ та ДМ Одеського національного морського університету, доктор технічних наук, професор.
К70 Нарисна геометрія та інженерна графіка. Частина І: навчальний
посібник/ М.В. Корх. – Одеса: НУ «ОМА», 2017. – 131с.
Навчальний посібник виконано згідно з навчальною програмою «Нарисна геометрія та інженерна графіка» і спрямований на покращення знань, умінь та творчості при опануванні конструкторської документації. У навчальному посібнику подано теоретичні відомості з кожної теми курсу геометричних креслень та нарисної геометрії, запропоновані запитання та завдання для самоперевірки знань, проведено детальний аналіз та наведена методика розв’язування задач, які допоможуть курсантам (студентам) навчатися самостійно розв’язувати типові задачі та виконувати розрахунково-графічні роботи.
Посібник призначений для курсантів (студентів) вищих навчальних закладів, які навчаються за спеціальностями: 271 – «Річковий та морський транспорт», спеціалізація – «Судноводіння», залузь знань – 27 «Транспорт». 271 – «Річковий та морський транспорт», спеціалізація – «Експлуатація суднових енергетичних установок», залузь знань – 0701 «Транспорт і транспортна інфраструктура». 151 – «Автоамтизація та комп’ютерно інтегровані технології», спеціалізація – автоматизовані управління судновими енергетичними установками, галузь знань – 15 «Автоматизація та приладобудування». 271 – «Річковий та морський транспорт», галузь знань – 27 «Транспорт», спеціалізація – «Експлуатація суднового електрообладнання і засобів автоматики».
Посібник буде корисним курсантам (студентам) вищих технічних навчальних закладів для освітнього ступеня «Бакалавр» і викладачам при організації самостійної роботи курсантів (студентів).
УДК 744:004.92
© М.В. Корх, 2017
ЗМІСТ
ВСТУП………………………………………………………………………….6
ПОЗНАЧЕННЯ Й СИМВОЛИ………………………………..…………….9
1. ОСНОВИ НАРИСНОЇ ГЕОМЕТРІЇ........................................................10
1.1.МЕТОДИ ПРОЕКТУВАННЯ………………………...….……………..10
1.1.1. Предмет нарисної геометрії………………………………………….10
1.1.2. Загальні характеристики методів проектування…………...………10
1.1.3. Епюр Монжа………………………………………………………..….11
1.1.4. Комплексне креслення…………… …………………………..………12
Запитання для самоперевірки знань…………………………...…………….13
Завдання для самоперевірки……………………………………….…………14
1.2. ПРЯМІ ЛІНІЇ……………………………………………………...……..15
1.2.1. Класифікація прямих ліній…………………………… ..………………15
1.2.2. Сліди прямої лінії…………………………………...…………………18
1.2.3. Визначення дійсної величини відрізка прямої методом прямокутного трикутника……………………………………………………………………….….19
1.2.4. Взаємне розташування прямих……………………………………….20
Запитання для самоперевірки знань…………………………...…………….21
Завдання для самоперевірки………………………………….………………22
1.3. ПЛОЩИНИ……………………………………………….………….…23
1.3.1. Загальні характеристики площин…………………………………….23
1.3.2. Визначення належності лінії та точки до площини…………………29
1.3.3. Головні лінії площини………………………… …………………….30
1.3.4. Взаємне розташування прямої та площини……………………….…31
1.3.5. Взаємне розташування площин…………………………………..…..33
Запитання для самоперевірки знань…………………………...…………….35
Завдання для самоперевірки……………………………….…………………36
1.4. МЕТОДИ ПЕРЕТВОРЕННЯ ПРОЕКЦІЙ……………………….…38
1.4.1. Загальні характеристики методів перетворення проекцій…….……38
1.4.2. Метод обертання…………………………………………………….…38
1.4.3. Суміщення……………………………………………………...………40
1.4.4. Метод заміни площин проекцій……………………...……………….41
1.4.5.Визначення відстані між двома паралельними прямими ……….…..44
Запитання для самоперевірки знань…………………………...…………….45
Завдання для самоперевірки……………………………………………….…45
1.5. БАГАТОГРАННИКИ……………………………………….……….…47
1.5.1. Загальні характеристики багатогранників…………...………………47
1.5.2.Побудова лінії перетину багатогранника площинами особливого положення……………………………………………………………….………….47
1.5.3. Побудова точки перетину багатогранника прямою лінією….….….50
1.5.4. Побудова лінії перетину двох багатогранників………………….…..53
Запитання для самоперевірки знань…………………………...…………….54
Завдання для самоперевірки………………………………………….………55
1.6. РОЗГОРТКА БАГАТОГРАННИКІВ………………..………….……56
1.6.1. Загальні характеристики розгорток багатогранників……………….56
1.6.2. Розгортка піраміди методом трикутника…………………...………..56
1.6.3. Розгортка призм методом розкатки………………………………..…58
1.6.4. Розгортка призми довільного розташування методом нормального перерізу………………………………………………………………………….…..61
Запитання для самоперевірки знань…………………………...…………….64
Завдання для самоперевірки………………………………………….………64
1.7. КРИВІ ЛІНІЇ……………………………………………………….….…65
1.7.1. Загальні характеристики кривих ліній……………………………….65
1.7.2. Визначення типу кривої лінії……………………………………..…..66
1.7.3. Визначення радіуса кривини кривої лінії методом кола………...….67
1.7.4. Побудова гвинтової лінії…………………………………...……..…..68
Запитання для самоперевірки знань…………………………...…………….69
Завдання для самоперевірки………………………………….………………69
1.8. ПОВЕРХНІ…………………………………………………………....….70
1.8.1. Загальні характеристики виконання поверхонь……………………..70
1.8.2. Побудова лінії перетину поверхні обертання площиною особливого положення……….………………………………………………...…………..……71
1.8.3. Побудова точки перетину поверхні обертання прямою лінією…….77
1.8.4. Побудова лінії перетину двох поверхонь обертання методом січних площин та методом січних куль…………………………………………………...77
Запитання для самоперевірки знань…………………………...…………….79
Завдання для самоперевірки…………………………………………….……80
2. ЗАГАЛЬНІ ПРАВИЛА ВИКОНАННЯ КРЕСЛЕНЬ…………………81
2.1. ВИДИ КОНСТРУКТОРСЬКИХ ДОКУМЕНТІВ………….……....81
2.2. ВИМОГИ СТАНДАРТІВ ДО ОФОРМЛЕННЯ КРЕСЛЕНЬ…..…81
2.2.1. Формати (ГОСТ 2.301 – 68)……………………………………………82
2.2.2. Масштаби (ГОСТ 2.302 – 68)…………………………………….…….86
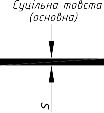
2.2.3. Лінії креслення (ГОСТ 2.303 – 68)………………………………...…..86
2.2.4. Шрифти креслярські (ГОСТ 2.304 – 81)………………………..…….88
2.2.5. Графічне позначення матеріалів на кресленнях (ГОСТ 2.306 – 68)…90
2.2.6. Нанесення розмірів (ГОСТ 2.307 – 68)………………………………..93
Запитання для самоперевірки…………………………………………………....109
Завдання для самостійної роботи…………………………………………….109
2.3. ГЕОМЕТРИЧНІ ПОБУДОВИ…………………………………….….110
2.3.1. Поділ відрізка на дві рівні частини……………………….……….110
2.3.2. Побудова перпендикуляра до прямої з точки, яка лежить поза прямою………………………………………………………………………….….112
2.3.3. Поділ кола на три рівних частини………………………………..….112
2.3.4. Поділ кола на п’ять рівних частин…………………………….…..113
2.4.5. Поділ кола на шість рівних частин…………………………………..114
2.3.6. Нахил………………………………………………………..………….114
2.3.7. Конусність……………………………………………………………..116
2.3.8. Спряження…………………………………………………….……..117
2.3.8.1. Спряження прямих ліній, які перетинаються за допомогою дуги…………………………………………………...……………………………118
2.3.8.2. Спряження паралельних прямих дугою кола………………..…119
2.3.8.3. Спряження дуги кола радіуса R і прямої а дугою заданого радіуса R1………………………………………………………………….……..120
2.3.8.4. Спряження дуг двох кіл за допомогою прямої лінії…….…120
2.3.8.5. Побудова спряження двох дуг кіл……………………………..122
2.3.8.6. Побудова спряження двох дуг кіл дугою заданого радіуса…123
Запитання для самоперевірки………………………………………………...….129
Завдання для самостійної роботи………………………………………...….….129
Література……………………………………………….………………….130
ВСТУП
Нарисна геометрія та інженерна графіка належить до дисциплін, які складають загальноінженерну підготовку спеціалістів із вищою технічною освітою.
Мета дисципліни - дати курсантам (студентам) знання, уміння та навички, необхідні майбутньому інженеру для викладання технічних ідей за допомогою креслення.
Предметом дисципліни є складання та читання креслень (графічних моделей) геометричних образів, що є в основі технічних виробів та креслень самих виробів.
До задач «Нарисної геометрії та інженерної графіки» слід віднести:
1) вивчення теоретичних основ побудови зображень точок, прямих, площин, поверхонь тощо;
2) розв’язання задач на взаємну належність та взаємний перетин геометричних образів та визначення їх натуральних величин;
3) вивчення способів побудови зображень предметів і деталей у відповідності зі стандартами;
4) розвиток уміння визначати геометричні форми простих деталей за їх зображенням та виконання цих зображень як з натури, так і за кресленням складальної одиниці;
5) вироблення навиків читання креслень складальних одиниць, а також умінь виконувати їх креслення у відповідальності зі стандартами України.
Нарисна геометрія та інженерна графіка є учбовою дисципліною, що складається з розділів нарисної геометрії, геометричних креслень та інженерної графіки.
Нарисна геометрія вивчає проектування геометричних фігур, з яких складаються елементи виробу, на площину. Вона є граматикою креслення і ефективно розвиває просторове уявлення.
Геометричне креслення вивчає графічні методи розв’язування геометричних задач на площині за допомогою креслярських інструментів.
Інженерна графіка вивчає перелік вимог, яких потрібно дотримуватись при виконанні конструкторської документації. Останні запропоновані: Державні стандарти України (ДСТУ), Галузеві стандарти України (ГСТУ) і Стандарти підприємства (СТП). Вони охороняються законами України.
Навчальний посібник підготовлений відповідно до навчальної програми „Нарисна геометрія та інженерна графіка” та призначений для оволодіння курсантами першого курсу знаннями з розділу „Нарисна геометрія”, „Геометричні побудови”.
У результаті вивчення розділу нарисної геометрії курсант (студент) повинен знати:
- Методи проектування геометричних фігур, центральне та паралельне (ортогональне).
- Прямокутні проекції основних геометричних фігур: проекція точки, прямої, площини.
- Побудови проекцій та взаємне розташування геометричних фігур: ліній, ліній і площин, головні лінії площин, двох площин, а також визначення ліній перетину двох площин та точки перетину прямої з площиною.
- Побудови дійсної величини відрізка прямої методом прямокутного трикутника.
- Методи перетворення креслення (обертання та заміна площин проекцій).
- Перетин багатогранника площиною та прямою. Взаємний перетин багатогранників. Розгортка багатогранників.
- Утворення та основні параметри проектування кривих ліній.
- Способи утворення поверхні. Поверхні обертання. Гвинтові поверхні.
- Переріз поверхні обертання площиною. Перетин поверхні прямою лінією. Перетин двох поверхонь обертання.
- Перетин поверхонь обертання з багатогранником.
- Призначення креслярських інструментів і приладдя при виконанні креслень.
- Основні прийоми виконання геометричних побудов.
- Прийоми виконання циркульних спряжень.
- Основні стандартні форми креслень.
- Стандартні масштаби зображень і їх позначення на кресленнях.
- Призначення та параметри ліній на кресленнях.
- Основні правила виконання зображень предметів і їх позначення на кресленнях.
- Стандартні графічні позначення матеріалів у перерізах.
- Правила нанесення розмірів на кресленнях.
На основі набутих знань курсанти (студенти) повинні вміти:
- Зображати геометричні фігури на кресленні за допомогою ортогонального проектування.
- Уявляти форму і положення геометричної фігурі у просторі за її проекційним зображенням.
- Будувати ортогональні проекції точки, лінії, прямої, площини.
- Будувати проекції ліній перетину площин і точки перетину прямої з площиною.
- Визначати дійсну величину геометричної фігури методами прямокутного трикутника, обертання та заміною площин проекцій.
- Виконувати переріз багатогранника площиною, лінію перетину двох багатогранників.
- Будувати розгортки багатогранників.
- Проектувати криві лінії, виконувати гвинтову лінію.
- Задавати та проектувати поверхні.
- Виконувати переріз площиною поверхні обертання, перетин поверхні обертання прямою лінією, перетин двох поверхонь обертання, перетин поверхні обертання з багатогранником.
- Користуватись креслярськими інструментами при виконанні креслень.
- Виконувати геометричні побудови – поділяти відрізки на рівні частини чи у задовільному відношенні, будувати перпендикулярні прямі.
- Будувати цуркульні спряження за даними умовами.
- Виконувати креслення предметів за правилами і вимогами державних стандартів.
- Виконувати написи на кресленнях стандартним шрифтом.
- Будувати третю проекцію предмета за двома заданими.
- Визначати необхідні зображення для виконання креслень предмета.
- Наносити розміри на кресленнях відповідно до правил державних стандартів.
Знання, уміння і навики, придбані в курсі нарисної геометрії та інженерної графіки, необхідні для вивчення загальноінженерних і спеціальних технічних дисциплін, а також в подальшій інженерній діяльності.
Навчальний посібник містить вступ, основний текст, запитання та завдання для самоперевірки знань, перелік завдань для виконання розрахунково-графічних робіт (РГР).
Основні теми:
1. Методи проектування.
2. Прямі лінії.
3. Площини.
4. Методи перетворення проекцій.
5. Багатогранники.
6. Розгортка багатогранників.
7. Криві лінії.
8. Поверхні.
Завдання до розрахунково-графічної роботи з нарисної геометрії
1. Визначення дійсної величини відрізка прямої методом прямокутного трикутника.
2. Побудова лінії перетину двох площин заданих слідами. Побудова точки перетину прямої лінії з площиною.
3. Побудова лінії перетину двох трикутників.
4. Побудова лінії перетину багатогранника площиною. Визначення дійсної величини геометричних фігур у перерізі.
5. Розгортка багатогранника одним з існуючих методів.
6. Побудова лінії перетину двох поверхонь обертання. Перетин поверхні обертання з багатогранником.
7. Побудова третьої проекції по двом заданим. Простановка розмірів на кресленні.
8. Побудова спряження двох прямих. Побудова спряження прямої з колом.
ПОЗНАЧЕННЯ Й СИМВОЛІКА
П — площина;
П1 — горизонтальна площина проекцій;
П2 — фронтальна площина проекцій;
П3 — профільна площина проекцій;
OX; OY; OY1; OY3; OZ — осі, отримані при перетині площин проекцій;
А, В, С, D.. — точки в просторі;
A1, B1, C1 — горизонтальні проекції точок;
A2, B2, C2 — фронтальні проекції точок;
A3, B3, C3 — профільні проекції точок;
[AB] — відрізок прямої;
[AB) — промінь прямої;
(AB) — пряма, яка проходить через дві точки;
|AB| — довжина відрізка між точками A і B;
R, P, F… — площини загального положення;
R12, P12, F12 — точки збігу слідів;
h1 — горизонтальний слід площини загального положення;
f2 — фронтальний слід площини загального положення;
p3 — профільний слід площини загального положення;
(MN) — лінія найбільшого нахилу;
∆, α, β, γ… — площини особливого положення;
∆12, α12, β12, γ12… — точки збігу слідів;
∩ — перетин прямих;
|| — паралельні прямі;
- — мимобіжні прямі;
- — належність;
— об’єднання;
— кон’юнкція (сполучник «і»);
— диз’юнкція (сполучник «або»);
— імплікація логічного наслідку «Якщо, то…»;
а, b, с, d, e — прямі та криві лінії;
Ф — поверхні;
A Ф — точка А належить до фігури Ф;
А Ф — точка А не належить до фігури Ф;
Фk ≡ Фi — фігури Фk та Фi збігаються;
Фk ≠ Фi — фігури Фk та Фi не збігаються;
Фk ∩ Фi — перетин фігур Фk та Фi;
Фk Фi — об’єднання фігур Фk та Фi.
РОЗДІЛ 1. ОСНОВИ НАРИСНОЇ ГЕОМЕТРІЇ
1.1. МЕТОДИ ПРОЕКТУВАННЯ
1.1.1. Предмет нарисної геометрії.
1.1.2. Загальні характеристики методів проектування.
1.1.3. Епюр Монжа.
1.1.4. Комплексне креслення.
1.1.1. Предмет нарисної геометрії
Нарисна геометрія, яка є одним із розділів математики, вивчає методи зображення тривимірного простору на площині, а також способи графічного розв’язання задач за рисунком.
Предметом нарисної геометрії є різноманітність геометричних образів та співвідношень між ними. Розрізняють три види геометричних образів: лінійні
(точка, пряма, площина), нелінійні ( крива лінія, крива поверхня) та складені
(багатогранники).
Основним елементом або образом тривимірного простору прийнято вважати точку. Довільну множину точок називають геометричною фігурою. Основними геометричними фігурами, крім точки, є ще пряма та площина.
Розрізняють два співвідношення між фігурами: позиційні та метричні. Позиційна властивість визначає розміщення геометричних фігур на площині та в просторі на основі взаємної належності одних фігур до інших. Належність може бути повною ( пряма лежить у площині), частковою ( пряма перетинається з площиною в точці) або її може не бути взагалі ( дві мимобіжні прямі).
Метричні властивості пов’язуються з визначенням метричних характеристик ( розмірів) відстаней, кутів та площ. Залежно від характеру властивостей розрізняють позиційні та метричні задачі.
1.1. 2. Загальні характеристики методів проектування
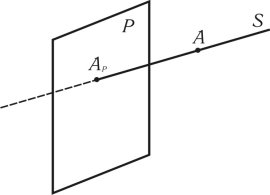
Рис. 1.1
Кожний об’ємний предмет має три виміри: довжину, ширину та висоту. Виготовляють предмети за кресленнями, що містять їх зображення, на площині (на аркуші паперу). За основу побудови зображень на кресленнях взято метод проектування. Він полягає в тому, що зображення предмета на площині дістають за допомогою проектувальних променів. Проектування нагадує утворення тіні предмета. При освітленні сонячними променями будь-який предмет (дерево, паркан, будівля) відкидає тінь. Вона подібна до обрисів самого предмета. Якщо предмет розмістити перед плоскою стінкою й освітити його ліхтариком, то на стінці утвориться тінь цього предмета. Утворений світловими променями контур предмета на площині можна вважати його проекцією.
Утворення зображення предмета на кресленні уявними проектувальними променями називається проектуванням. Утворене методом проектування зображення предмета на площині називається проекцією. Площина, на якій одержано проекцію, називається площиною проекцій.
Залежно від взаємного розміщення проектувальних променів у просторі розрізняють центральне і паралельне проектування.
Якщо проектувальні промені виходять з однієї точки, то проектування називаються центральним. Точка, з якої виходять промені, називається центром проектування. Проекція, утворена центральним проектуванням, називається центральною.
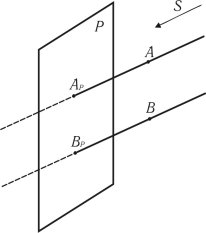
Для застосування центрального проектування (рис.1.1) потрібно знати точку в просторі А, центр проектування S і площину P, на яку проектується точка А. З центру проектування проводиться проектувальний промінь до перетину з площиною проекцій, точка перетину Ар є проекцією точки А на площині Р. Проекція точки — це відображення точки, яка знаходиться в просторі, на площину. [SA] ∩ P = Ap.
Паралельним проектуванням називають проектування точки на площину, коли центр проектування віддалений від площини в безмежність і коли проектувальні промені [ВВр) і [AAp) стають паралельними. Для здійснення паралельного проектування потрібні наступні складові:
Р — площина проекції;
А — точка в просторі;
В — точка в просторі;
S — напрям проектування.
Проекції утворюються за допомогою проектувальних променів, проведених паралельно напрямку проектування S.
На рис. 1.2 показано побудову проекцій точок А і В паралельним проектуванням: [AAP) ∩ P = AP — проекція точки А на площину Р. [ВВP) ∩ P = ВP — проекція точки В на площину Р.
У випадку коли проектувальний промінь направлений перпендикулярно до площини проекцій, таке проектування називається ортогональним.
1.1.3. Епюр Монжа (креслення)
Гаспар Монж запропонував проектувати точку на дві взаємно перпендикулярні площини проекцій за допомогою ортогонального проектування.
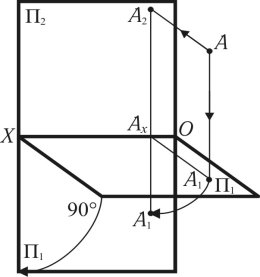
Рис. 1.3
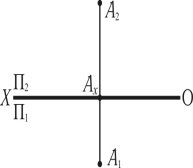
Рис. 1.4
Здійснення такого проектування доцільно розглядати на просторовій моделі (рис. 1.3), де П2 — фронтальна площина проекцій, П1 — горизонтальна площина проекцій. Вони перетинаються по осі (ОХ). З точки А, яка знаходиться в просторі, проводяться проектувальні промені до перетину з відповідними площинами. Точка перетину проектувального променя з площиною визначає проекцію точки A2 — фронтальна проекція точки A, A1 — горизонтальна проекція точки A. Лінії [А2Ах] і [А1Ах] називаються лініями проектувального зв’язку. Вони показують відстань точки А від відповідної площини проекцій: [A2Ax] — відстань точки А від площини П1; [A1Ax] — відстань точки А від площини П2.
Для того, щоб від просторової моделі перейти до площинної, необхідно горизонтальну площину проекцій повернути на кут 90о вниз відносно осі (ОХ), тоді вона стане продовженням площини П2. Площинна модель називається епюром Монжа або кресленням (рис. 1.4).
1.1.4. Комплексне креслення
Комплексним кресленням називається проектування точки на три взаємно перпендикулярні площини проекцій, для чого проводиться фронтальна площина проекцій П2 перпендикулярно до П1 — горизонтальної площини проекцій. Площини перетинаються між собою по осі (ОХ). Перпендикулярно до горизонтальної та фронтальної площини проекцій проводиться профільна площина проекцій П3, яка перетинає площину П2 і утворює вісь (ОZ): П3 ∩ П2 = (ОZ), П3 ∩ П1 = (ОY).
На (рис. 1.5) наведено комплексне креслення на просторовій моделі.
Проектування точки A, яка знаходиться в просторі на П1, П2 і П3 здійснюється за допомогою ортогонального проектування. Лінії проектувального зв’язку [A2Ax], [A1Ax] розглядались на просторовій моделі Г. Монжа.
Проекція А3 знаходиться в площині П3, тому її фронтальна проекція Аz буде знаходитись на осі (ОZ). Довжина відрізка [A2Az] показує відстань
точки А від площини П3. Для перетворення просторової моделі на
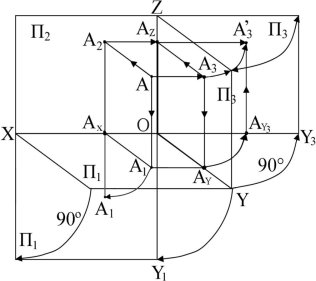
Рис. 1.5
площинну слід повернути площину П1 вниз відносно осі (ОХ) на 90º, площина П3 повертається навколо осі (ОZ) на 90º проти годинникової стрілки. При перетворені просторової моделі на площинну вісь Y поділяється на (OY1) i (OY3). Площинна модель називається комплексним кресленням.
Побудова третьої проекції точки по двом заданим виконується на комплексному кресленні за допомогою ліній постійного нахилу (ЛПН). Побудови видно з комплексного креслення (рис. 1.6).
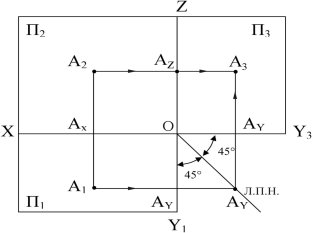
Рис. 1.6
Запитання для самоперевірки знань
1. Що вивчає нарисна геометрія?
2. Які способи проектування використовуються в нарисній геометрії?
3. У чому полягає суть способу паралельного проектування?
4. У чому полягає суть способу ортогонального проектування?
5. Як задати точку в площині?
6. Як побудувати профільну проекцію точки по горизонтальній та фронтальній проекціях?
Завдання для самоперевірки
Задача № 1
По координатам точки А: х=30мм,
у=20мм,
z =15мм,
побудувати три її проекції на комплексному креслені.
Задача №2
По двом проекціям А1 і А2 точки А побудувати профільну проекцію.
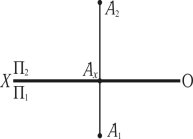
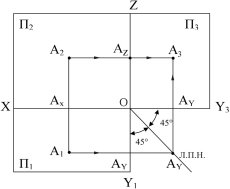
Задача №3
Чому дорівнює відстань точки А в просторі до кожної з площин проекцій П1, П2 та П3?
1.2. ПРЯМІ ЛІНІЇ
1.2.1. Класифікація прямих ліній.
1.2.2. Сліди прямої лінії.
1.2.3. Визначення дійсної величини відрізка прямої методом прямокутного трикутника.
1.2.4. Взаємне розташування прямих.
1.2.1. Класифікація прямих ліній
Залежно від розташування прямих відносно площин проекцій вони поділяються на прямі загального положення і прямі особливого положення.
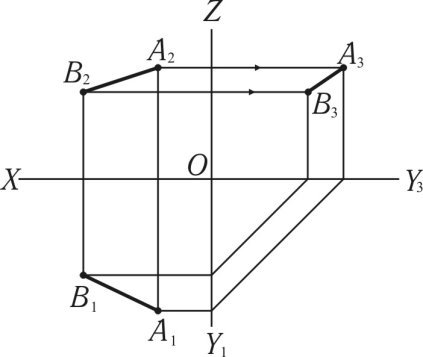
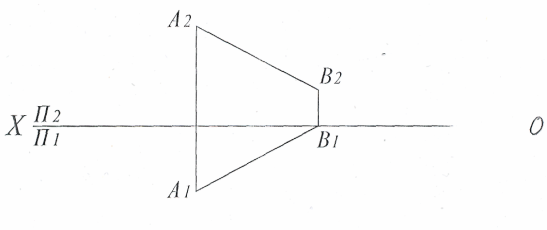
Прямі лінії загального положення — це лінії, які не паралельні ні одній з площин проекцій. Відрізки таких ліній проектуються на площини проекцій зі спотворенням. Відрізок такої прямої лінії представлений на рис. 1.7 в системі площин проекцій, коли П2∩П1 і (П3∩П2)(П3∩П1). З креслення видно, що відрізок прямої лінії не паралельний ні одній з площин проекцій.
Рис. 1.7
Прямі лінії особливого положення поділяються на прямі рівня і прямі проектувальні.
Прямі лінії рівня — це лінії, які паралельні до однієї площини проекцій і проектуються на неї в дійсну величину. Відрізок горизонтальної прямої лінії [AB] (рис. 1.8) — це пряма лінія, яка паралельна горизонтальній площині проекцій П1, горизонтальна проекція прямої лінії [A1B1] є дійсна величина.
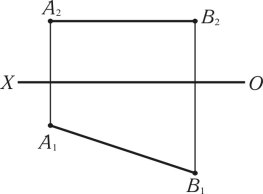
Рис. 1.8
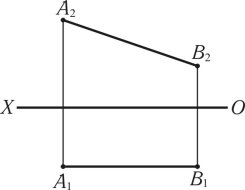
Рис. 1.9
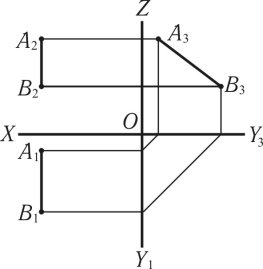
Рис. 1.10
Відрізок фронтальної прямої лінії [AB] (рис. 1.9) — це пряма лінія, яка паралельна фронтальній площині проекцій П2, фронтальна проекція прямої лінії [A2B2] є дійсна величина.
Відрізок профільної прямої [AB] (рис. 1.10) — це пряма лінія, яка паралельна профільній площині проекцій П3, профільна проекція прямої лінії [A3B3].
Проектувальні прямі лінії — це лінії, які паралельні двом площинам проекцій або перпендикулярні до однієї площини. Відрізки таких прямих проектуються на дві площини проекцій в дійсну величину.
Горизонтально-проектувальна пряма лінія (рис. 1.11) — це лінія, яка перпендикулярна до горизонтальної площини проекцій і проектується на неї в точку A1B1. Фронтальна проекція прямої [A2B2] є дійсна величина.
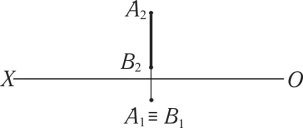
Рис. 1.11
Фронтально-проектувальна пряма лінія (рис. 1.12) — це лінія, яка перпендикулярна до фронтальної площини проекцій і проектується на неї в точку A2B2. Горизонтальна проекція прямої лінії [A1B1] є дійсна величина.
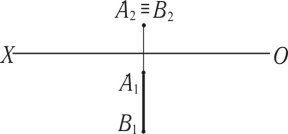
Рис. 1.12
Профільно-проектувальна пряма лінія (рис. 1.13) — це лінія, яка перпендикулярна до профільної площини проекцій і проектується на неї в точку A3B3. Горизонтальна [A1B1] та фронтальна [A2B2] проекції прямої лінії проектуються в дійсну величину.
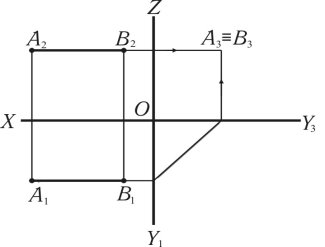
Рис. 1.13
1.2.2. Сліди прямої
Слідом прямої лінії називається точка перетину лінії з площиною проекцій. Це видно на просторовій моделі (рис. 1.14): М — фронтальний слід, він збігається з фронтальною проекцією фронтального сліду М ≡ М2; N — горизонтальний слід, він збігається з горизонтальною проекцією горизонтального сліду N ≡ N1. Для побудови на кресленні проекцій відповідних слідів прямої лінії необхідно спроектувати фронтальну і горизонтальну проекції слідів на вісь (ОX) які перетині з віссю визначать фронтальну проекцію горизонтального сліду N2 та горизонтальну проекцію фронтального сліду М1.
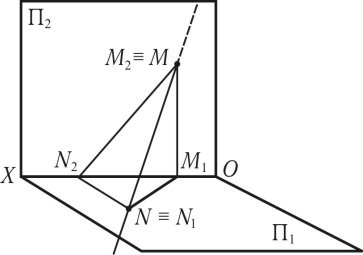
Рис. 1.14
Поєднання фронтальної проекції фронтального сліду М2 з фронтальною проекцією горизонтального сліду N2, визначає фронтальну проекцію лінії (N2M2). Поєднання горизонтальної проекції горизонтального сліду N1 з горизонтальною проекцією фронтального сліду М1 визначає горизонтальну проекцію лінії (N1M1).
Побудову слідів прямої (AB) на кресленні показано на рис. 1.15. Пряму задано проекціями [A2B2][A1B1].
Для визначення фронтальної проекції фронтального сліду потрібно горизонтальну проекцію [A1B1] продовжити до перетину з віссю (ОХ). В точці M1 ставиться перпендикуляр до осі (ОХ) і продовжується до перетину з продовженням [A2B2]. Точка перетину визначає фронтальну проекцію фронтального сліду М2, фронтальний слід М2 збігається з самим слідом М2=М.
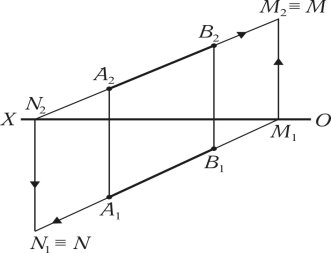
Рис. 1.15
Для побудови горизонтального сліду необхідно продовжити [A2B2] до перетину з віссю (ОХ), точка перетину визначає фронтальну проекцію горизонтального сліду N2. З точки N2 проводиться перпендикуляр до перетину з продовженням проекції [A1B1], точка перетину N1 визначає горизонтальну проекцію горизонтального сліду, яка збігається з самим слідом N = N1.
1.2.3. Визначення дійсної величини відрізка прямої методом прямокутного трикутника
Для визначення дійсної величини відрізка прямої лінії (рис. 1.16) методом прямокутного трикутника потрібно побудувати прямокутний трикутник, один катет якого дорівнює проекції відрізка прямої, а другий катет дорівнює різниці відстаней кінців відрізка прямої від відповідних площин проекцій. Гіпотенуза такого трикутника ![]() дорівнює дійсній величині відрізка прямої лінії, 1 — кут нахилу прямої (AB) до площини П1, 2 — кут нахилу відрізка прямої до площини П2. Побудову дійсної величини відрізка прямої видно з алгоритму.
дорівнює дійсній величині відрізка прямої лінії, 1 — кут нахилу прямої (AB) до площини П1, 2 — кут нахилу відрізка прямої до площини П2. Побудову дійсної величини відрізка прямої видно з алгоритму.
1. [A1B1]![]() | B1
| B1![]() 1| = |B2BX| - |A2Ax|
1| = |B2BX| - |A2Ax|
2. ![]() — дійсна величина [AB]
— дійсна величина [AB]
3. (AB)∩П1 = 1 — кут нахилу з площиною П1
4. [A2B2]![]() |B2
|B2![]() 2| = |A1Ax| - |B1Bx|
2| = |A1Ax| - |B1Bx|
5. ![]() — дійсна величина [AB]
— дійсна величина [AB]
6. (AB)∩П2 = 2 — кут нахилу до площини П2
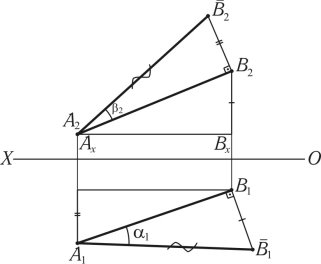
Рис. 1.16
1.2.4. Розташування прямих ліній в просторі
Прямі лінії в просторі можуть бути: паралельними, перетинними і мимобіжними.
|
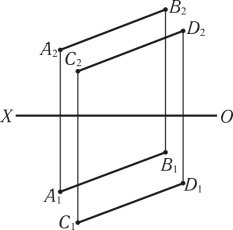
Паралельні прямі. Якщо прямі лінії паралельні в просторі, то їх проекції на всіх площинах проекцій повинні бути паралельними між собою (рис. 1.17).
(AB) || (CD) {[A1B1] || [C1D1]} {[A2B2] || [C2D2]} |
|
||
|
|
Рис. 1.17 |
||
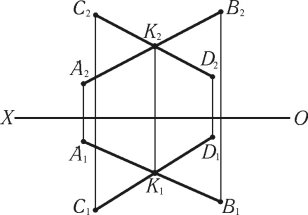
Перетинні прямі лінії. Якщо прямі лінії перетинаються між собою, то у них є спільна точка K, проекції якої повинні знаходитись на одній лінії проектувального зв’язку, перпендикулярній до осі (ОХ) (рис. 1.18) і належати до проекцій перетинних прямих.
|
(CD) ∩ (AB) = K [C1D1] ∩ [A1B1] = K1, [C2D2] ∩ [A2B2] = K2 |
|
|
|
Рис. 1.18 |
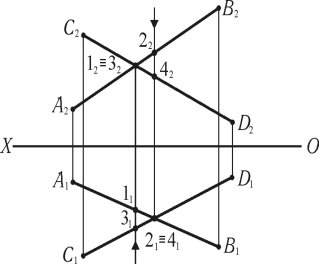
Мимобіжні прямі лінії. Якщо прямі лінії не мають спільної точки (рис. 1.19), то точки перетину їх проекцій належать до окремих ліній:
|
1 (AB); 3 (CD); 2 (AB); 4 (CD)
і проекції: 11 [A1B1]; 12 [A2B2]; 21 [A1B1]; 22 [A2B2]; 41 [C1D1]; 42 [C2D2].
|
|
Рис. 1.19
Для визначення видимості проекцій ліній в окремих точках застосовується метод конкуруючих точок, який полягає в тому (див. рис. 1.19), що з точки перетину відповідних проекцій ліній проводиться перпендикуляр до осі (OX) і продовжується до перетину з проекціями ліній на іншій площині проекцій. На кінці лінії ставиться стрілка. Проекція точки, яка розташована ближче до стрілки, буде на протилежній проекції видимою, відповідно і лінія, до якої належить точка, теж буде видимою в даній точці. Проекція точки, яка знаходиться далі від стрілки, буде належати до невидимої лінії.
Запитання для самоперевірки знань
1. Які прямі називаються прямими загального положення?
2. Які прямі належать до прямих особливого положення?
3. Що називається слідом прямої лінії?
4. Як розташовуються прямі лінії, відносно площин проекцій?
5. Як визначається натуральна величина відрізка прямої?
Завдання для самоперевірки
Задача №1
По заданому кресленню побудувати сліди прямої (АВ).
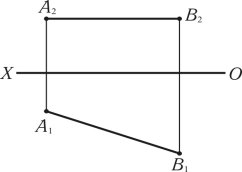
Задача №2
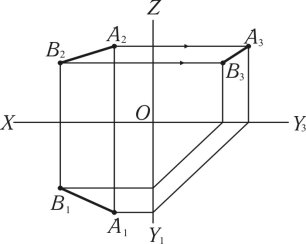
Визначити дійсну величину відрізка прямої (АВ) на фронтальній площині проекцій.
1.3. ПЛОЩИНИ
1.3.1. Загальні характеристики площин.
1.3.2. Визначення належності лінії та точки до площини.
1.3.3. Головні лінії площини.
1.3.4. Взаємне розташування прямої та площини.
1.3.5. Взаємне розташування площин.
1.3.1. Загальні характеристики площин
Площини на кресленні задаються одним із існуючих способів (рис.1.20):
а) трьома точками, які не належать до однієї лінії;
б) прямою і точкою, яка їй не належить;
в) двома перетинними прямими лініями; двома паралельними прямими лініями;
г) площинною фігурою;
е) слідами площини (рис. 1.21).
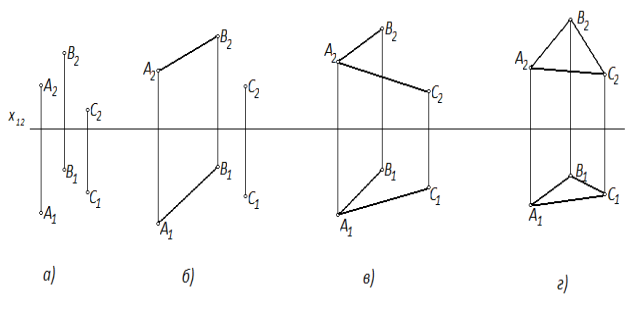
Рис. 1.20
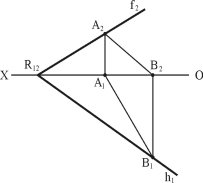
Слідом площини називається лінія перетину площини з площиною проекції. Площина R, задана слідами, показана на рис. 3.2:
f2 — фронтальний слід; h1 — горизонтальний слід; R12 — точка збігу слідів.
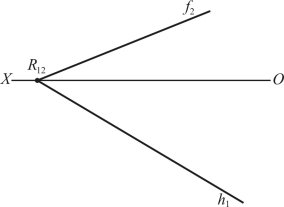
Рис. 1.21
У залежності від розташування площин відносно площин проекцій, площини поділяються на площини загального та площини особливого положення.
Площини загального положення (рис. 1.22) розташовані не паралельно і не перпендикулярно до площин проекцій. Сліди таких площин розташовані під гострими кутами до осей (OX); (OY); (OZ). На практиці часто доводиться по горизонтальному і фронтальному сліду виконувати профільний слід площини. Для цього достатньо провести фронтальний f2 і горизонтальний h1 сліди, визначити точки збігу слідів R12, R23, R13 на відповідних осях. За допомогою лінії постійного нахилу визначається точка збігу слідів R'13 на осі (OY3), поєднання точок збігу слідів R'13 R23 визначає профільний слід площини P3.
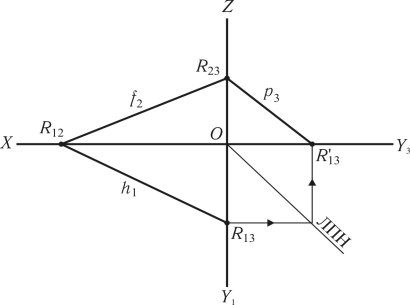
Рис. 1.22
Площини особливого положення – це площини паралельні або перпендикулярні до площин проекції.
У залежності від розташування площин відносно площин проекцій площини особливого поділяються на проектувальні площини і площини рівня.
Проектувальні площини — це площини, які перпендикулярні до однієї з площин проекцій. Вони мають збиральні властивості, тобто креслення, які належать до такої площини, проектуються на відповідний її слід. Такі площини поділяються на горизонтально-проектувальні, фронтально-проектувальні і профільно-проектувальні площини.
Горизонтально-проектувальна площина — це площина, яка перпендикулярна до горизонтальної площини проекцій (рис. 1.23),
а — просторова модель, б — креслення, П1 (A ), А1 1.
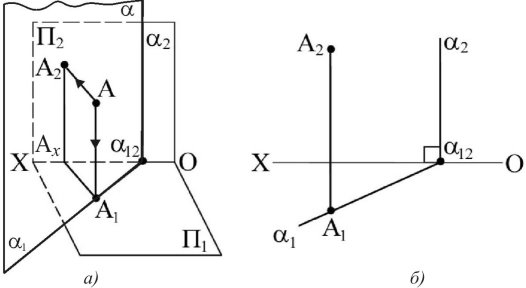
Рис. 1.23
Фронтально-проектувальна площина — це площина, яка перпендикулярна до фронтальної площини проекцій (рис. 1.24).
П2 (B2 2) П2 (B ) B2 2
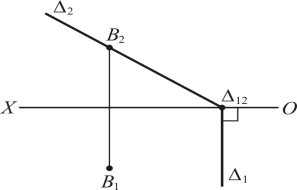
Рис. 1.24
Профільно-проектувальна площина — це площина, яка перпендикулярна до профільної площини проекцій (рис. 1.25), П3 (C ) C3 3. Профільний слід площини використовується для визначення по одній проекції точок інших. З креслення видно, як використовується профільний слід 3, якому належить C3, для визначення горизонтальної проекції C1.
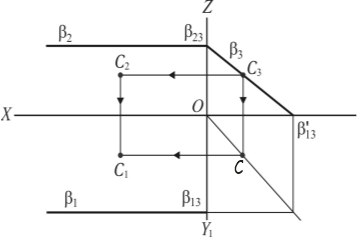
Рис. 1.25
Крім профільно-проектувальної площини, наведеної на кресленні (рис. 1.25), існують ще два випадки: у першому випадку профільно-проектувальна площина (2 1) (OX) проходить через вісь (ОХ) і нахилена під однаковими кутами 45° до площини П2 і П1. Така площина називається бісекторною (рис. 1.26).
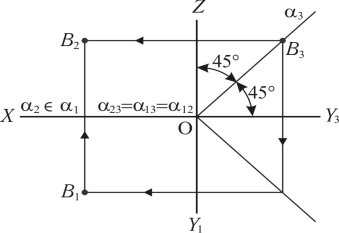
Рис. 1.26
Для побудови такої площини проводиться з точок збігу слідів α12, α13, α23 профільний слід площини α3 під кутом 45° до осі (OY3) і (OZ). Горизонтальна проекція B1 визначається за допомогою B3 3 і B2 за допомогою ліній проектувального зв’язку, що видно з креслення.
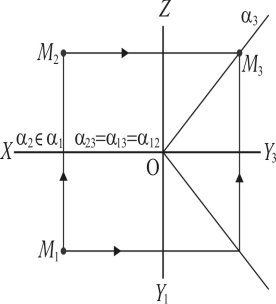
Рис. 1.27
У випадку, коли профільно-проектувальна площина (рис. 1.27) проходить через вісь (ОХ) і нахилена до площин П1 і П2 під різними кутами, для побудови профільного сліду такої площини α3 потрібно мати точку M, яка належить до площини . Для побудови 3 визначається профільна проекція M3, по двом заданим проекціям M2 і M1, через точки збігу слідів 23, α13 і M3 проводиться профільний слід площини 3. Побудови видно з креслення.
Площини рівня — це площини, які перпендикулярні до двох площин проекцій або паралельні до однієї площини. Вони мають збиральні властивості. Креслення, що належать до такої площини, проектуються на відповідні її сліди.
Горизонтальна площина — це площина, яка перпендикулярна до П2 і П3 і паралельна до горизонтальної площини проекцій (рис. 1.28), а — просторова модель. Будь-яка фігура розташована у такій площині, проектується на горизонтальну площину проекції в дійсну величину. Площина ∩ П2 = 2 — фронтальний слід площини, який паралельний осі (ОХ). Площина перетинає профільну площину проекцій П3 — утворює профільний слід 3. Перетин слідів 2 3 визначає точку збігу слідів 23 на осі (OZ). Точка А, яка належить до площини , проектується на сліди А2 2, а також на площину А1 П1. Проектування А1 і А3 на вісь (OY) визначає проекцію Аy. На рис. 1.28, б – показана горизонтальна площина на кресленні, де 2 — фронтальний слід площини , А2 і А1 — проекції точки А, яка належить до площини .
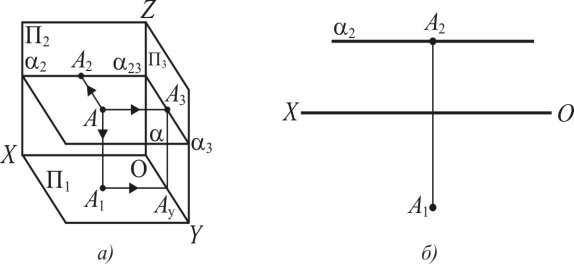
Рис. 1.28
Фронтальна площина — це площина, яка перпендикулярна до П1 і П3 а також паралельна до фронтальної площини проекцій. Будь-яка фігура розташована у такій площині, проектується на фронтальну площину проекції в дійсну величину. На кресленні (рис. 1.29) показано фронтальну площину рівня . || П2 1 || (OX), B B1 1.
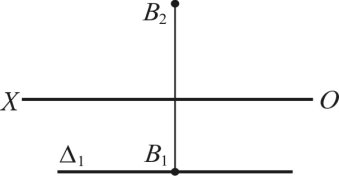
Рис. 1.29
Профільна площина — це площина, яка перпендикулярна до П2 і П1 і паралельна до профільної площини проекції (рис. 1.30). Будь-яка фігура розташована у такій площині, проектується на профільну площину проекції в дійсну величину || П3 2 || (OZ) 1 || (OY1), C C2 2 C1 1.
На рис. 3.11 показано, як знайдено горизонтальну і фронтальну проекції точки С (С1, С2) по її профільної проекції. Побудови видно з креслення.
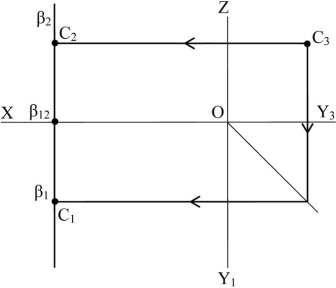
Рис. 1.30
1.3.2. Належність прямої лінії та точки до площини
Пряма лінія належить до площини, коли її відповідні сліди належать до відповідних слідів площин (рис. 1.31). Для побудови лінії (АВ), яка належить до площини R, проводяться сліди площини f2 h1, які перетинаються в точці збігу слідів R12, після чого проводиться пряма (AB) [A2B2, A1B1], проекції слідів якої А2 і В1 знаходяться на відповідних
слідах площини. Пряма (AB) задана відрізком прямої, якa належить до площини R.
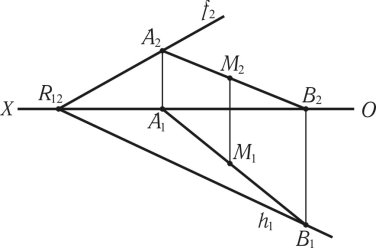
Рис. 1.31
Точка М (М2,М1) належить до площини R, тому що її відповідні проекції належать відповідним проекціям прямої (AB), яка належить до площини R, М2 [A2B2] М1 [A1B1].
1.3.3. Головні лінії площини
Головні лінії площини – це лінії, які належать до площини і паралельні одній площині проекцій (рис. 1.32 а, б). До таких ліній належать: горизонталь, фронталь та лінія найбільшого нахилу.
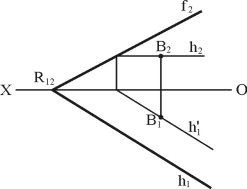
Горизонталлю називається лінія, яка належить до площини і паралельна горизонтальній площині проекцій, вона показана на (рис. 1.32) (а — просторова модель, б — креслення).
Для побудови горизонталі проводиться площина R (h1, f2, P3), після чого виконується горизонталь в просторі h паралельно горизонтальній площині проекції з слідами M2 і М3 (рис. 1.32, а), фронтальна проекція горизонталі паралельна осі h'2|| (OX). Горизонтальна проекція горизонталі h'2 паралельна горизонтальному сліду h1. На (рис. 1.32, б) показано побудову горизонталі на кресленні: h'2— фронтальна проекція горизонталі, h'2 паралельна (OX), h'1— горизонтальна проекція горизонталі, h'1 паралельна h1.
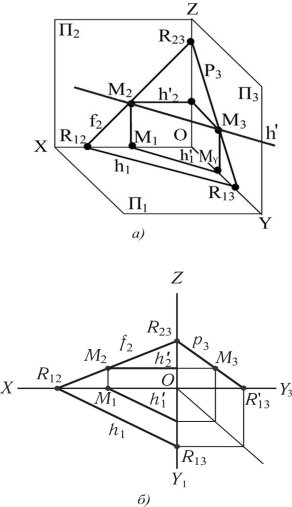
Рис. 1.32
Фронталлю називається лінія, яка належить до площини і паралельна фронтальній площині проекцій. Вона виконується аналогічно горизонталі. Побудову фронталі на кресленні наведено на рис. 1.33, f'1 — горизонтальна проекція фронталі, яка паралельна осі (ОХ); f'2 — фронтальна проекція фронталі, яка паралельна f2 .
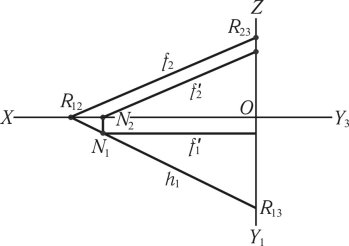
Рис. 1.33
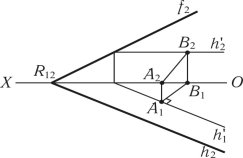
Лінією найбільшого нахилу (рис. 1.34) називається лінія, яка належить до площини і перпендикулярна до горизонталі площини. Для побудови лінії найбільшого нахилу використовується нульова горизонталь, горизонтальна проекція якої збігається з горизонтальним слідом h'1 h1, фронтальна проекція горизонталі збігається з віссю h'2 (OX). У площині R проводиться перпендикулярно до горизонтального сліду h’1 горизонтальна проекція (M1N1) лінії найбільшого нахилу. За допомогою ліній проектувального зв’язку визначаються фронтальні проекції N2 і M2, поєднання відповідних проекцій визначає фронтальну проекцію лінії найбільшого нахилу [N2M2] і [N1M1] – проекції лінії найбільшого нахилу (NM).
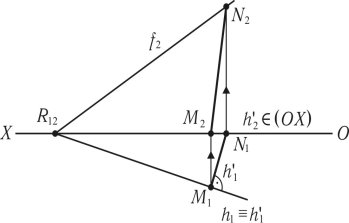
Рис. 1.34
1.3.4. Взаємне розташування прямої та площини
У залежності від розташування прямої відносно площини в просторі пряма може бути паралельною до площини або перетинати її.
Пряма паралельна до площини – така пряма, що повинна бути паралельною до прямої, що належить до площини (рис. 1.35) m || (MN) R (m2 || [M2N2]) (m1 || M1N1). Побудови видно з креслення.
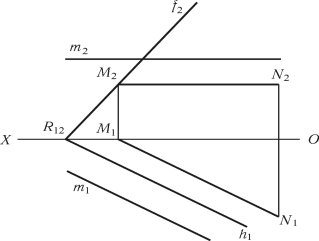
Рис. 1.35
Перетин площини прямою лінією – перша основна позиційна задача курсу нарисної геометрії. До неї можна звести більшість позиційних задач геометричними фігурами.
Побудову точки перетину прямої лінії з площиною розглянуто на прикладі перетину прямої m з площиною R (рис. 1.36).
Алгоритм визначення точки перетину прямої з площиною складається з трьох операцій:
-
Залучити пряму m в горизонтально-проектувальну площину
(12), m1 1; - Побудувати проекції лінії перетину площин (R ∩ ) = (1222) (1121);
- Визначити точку перетину фронтальної проекції лінії перетину (1222) з проекцією m2, де K2 — фронтальна проекція точки перетину, K1 — горизонтальна проекція, яка визначається за допомогою лінії проектувального зв’язку. Побудову точки перетину прямої з площиною видно з креслення та алгоритму:
![]() ) m П1 m1 1
) m П1 m1 1
![]() ) R ∩ = (1222) (1121)
) R ∩ = (1222) (1121)
![]() ) m2 ∩ (1222) = K2 → K1
) m2 ∩ (1222) = K2 → K1
![]() ) m ∩ R = K
) m ∩ R = K
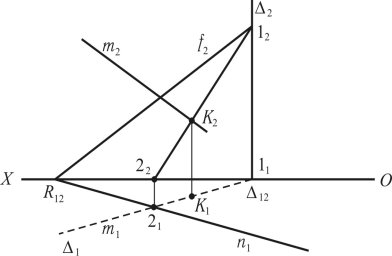
Рис. 1.36
1.3.5. Взаємне розташування площин
Дві площини в просторі можуть бути паралельними між собою або перетинатися.
Площини задані слідами паралельні, якщо відповідні сліди цих площин паралельні між собою (рис. 1.37).
R || Q (f2 || f΄'2) (h1 || h'1).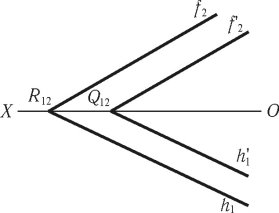
Рис. 1.37
Визначення лінії перетину площин – друга основна позиційна задача.
Площини перетинаються по прямій лінії. Для визначення такої лінії потрібно знати дві точки, які одночасно належать до обох площин, такі точки знаходяться на перетині відповідних слідів площин. На рис. 1.38 наведено просторову модель перетину двох площин загального положення, на якій показано, що фронтальна проекція точки перетину площин R ∩ Q знаходиться на перетині фронтальних слідів f '2 ∩ f2 = M2 M, горизонтальна проекція перетину площин R ∩ Q знаходиться на перетині горизонтальних слідів h1 ∩ h'1 = N1 N. M1 – горизонтальна проекція фронтального сліду; N2 – фронтальна проекція горизонтального сліду.
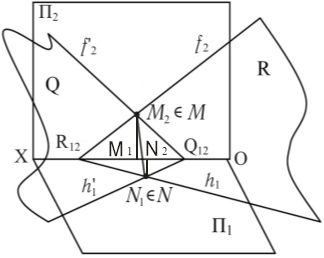
Рис. 1.38
Побудову лінії перетину двох площин загального положення на кресленні показано на рис. 1.39. Фронтальна проекція точки M2, яка належить до лінії перетину, визначається при перетині f2 ∩ f '2 = M2, горизонтальна проекція визначається при перетині h1 ∩ h'1 = N1, M1 і N2 визначаються за допомогою ліній проектувального зв’язку. R ∩ Q = (MN).
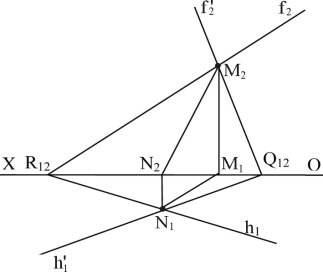
Рис. 1.39
На рис. 1.40 показано побудову лінії перетину площини загального положення з горизонтально-проектувальною площиною. Перетин фронтальних слідів f2∩2 = M2 визначає фронтальну проекцію M2, M1 визначається за допомогою лінії проектувального зв’язку, горизонтальну проекцію отримано при перетині 1∩h1 = N1, N2 визначається за допомогою лінії проектувального зв’язку. Фронтальна проекція лінії перетину — [M2N2], горизонтальна проекція лінії перетину — [M1N1]. У такому випадку горизонтальна проекція лінії перетину збігається з горизонтальним слідом площини , [M1N1] 1.
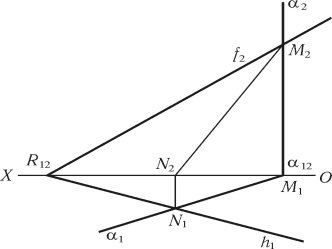
Рис. 1.40
На рис. 1.41 показано побудову лінії перетину площини загального положення R з горизонтальною площиною рівня . Площини перетинаються по горизонталі [M2N2] || (OX), [M1N1] || h1. Фронтальна проекція лінії перетину збігається зі слідом площини , [M2N2] 2.
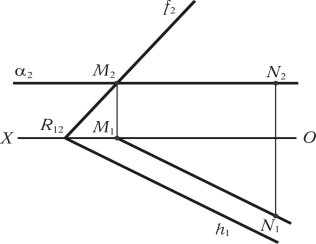
Рис. 1.41
Запитання для самоперевірки знань
1. Якими способами можна задавати площину на кресленні?
2. Що називається слідом площини?
3. Які площини належать до площин довільного та особливого положення?
4. Коли пряма лінія та точка належить до площини?
5. Які лінії належать до головних ліній площини?
6. Які випадки взаємного розташування двох площин в просторі існують?
Завдання для самоперевірки
Задача № 1
Визначити, чи належить пряма (AB) до площини (R)?
|
|
|
Задача № 2
Визначити, чи належить точка B до площини (R)?
|
|
|
Задача № 3
|
|
|
У площині R проведено лінію (AB). Чи є вона лінією найбільшого нахилу?
Задача № 4
Визначити, чи належить відрізок [AB] до площини ?
|
|
|
Задача № 5
Побудувати профільний слід профільно-проектувальної площини , яка має координати точок збігу слідів 23 [OZ] = 30 мм; 13 [OY1] = = 10 мм.
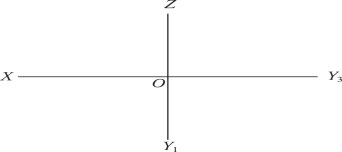
Задача № 6
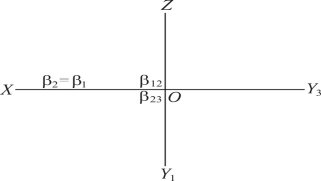
Побудувати профільний слід профільно-проектувальної площини , коли (OX) ≡ 2 ≡ 1 і площина бісекторна.
1.4. МЕТОДИ ПЕРЕТВОРЕННЯ ПРОЕКЦІЙ
1.4.1. Загальні характеристики методів перетворення проекцій.
1.4.2. Метод обертання.
1.4.3. Суміщення.
1.4.4. Метод заміни площин проекцій.
1.4.5.Визначення дійсної величини відстані між двома паралельними прямими методом заміни двох площин проекцій.
1.4.1. Загальні характеристики методів перетворення проекцій
В нарисній геометрії для вирішення деяких позиційних та метричних завдань доцільно перемістити заданий геометричний об’єкт (або об’єкти) у просторі із загального положення в особливе, у якому спрощується вирішення зазначеного завдання.
Наприклад, для визначення натуральної величини плоскої фігури її необхідно перемістити у просторі у положення, паралельне площині проекції, на котру вона спроектується у натуральну величину.
Для визначення відстані від точки до площини необхідно перемістити у просторі задані об’єкти (точку та площину) так, щоби площина стала проектуючою (перпендикулярній площині проекцій). У такому положенні відстань від точки до площини спроектується у натуральну величину на площину проекцій.
Для виконання таких переміщень геометричних об’єктів у просторі існує декілька способів визначення дійсної величини геометричних фігур: метод прямокутного трикутника, метод обертання, метод суміщення, метод заміни площин проекцій. Визначення дійсної величини відрізка прямої методом прямокутного трикутника розглядалося раніше і наведено в розділі 2.
1.4.2. Метод обертання
Для визначення натуральних величин плоских фігур доцільно використати їх обертання навколо горизонталі або фронталі до положення, паралельного П1 чи П2.
При застосуванні метода обертання геометрична фігура ставиться в положення, паралельне одній з площин проекцій, на яку проектується в дійсну величину. Для здійснення обертання необхідно знати наступні параметри: I2, I1 — вісь обертання, ![]() — центр обертання, r2, r1 — радіус обертання і 2 — фронтальний слід площини, в якій обертається точка, що належить до геометричної фігури. Обертання точки А навколо вертикальної осі І на кут 200º показано на рис. 1.42.
— центр обертання, r2, r1 — радіус обертання і 2 — фронтальний слід площини, в якій обертається точка, що належить до геометричної фігури. Обертання точки А навколо вертикальної осі І на кут 200º показано на рис. 1.42.
При обертанні точки А навколо осі І, перпендикулярної до площини П1, точка переміщається навколо осі по колу, яке проектується на горизонтальну площину проекцій в дійсну величину, на фронтальну — в пряму лінію ![]() , яка збігається зі слідом площини 2, [O΄1
, яка збігається зі слідом площини 2, [O΄1![]() 1] || (OX).
1] || (OX).
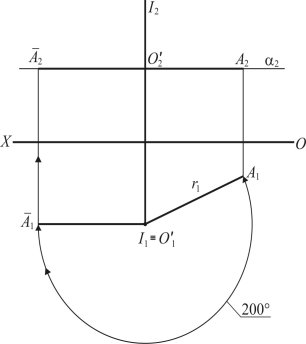
Рис. 1.42
Визначення дійсної величини відрізка прямої методом обертання навколо осі, перпендикулярної до площини
Обертання застосовується для визначення дійсної величини геометричної фігури, яка не паралельна площинам проекцій.
На рис. 1.43 показано, як здійснюється визначення дійсної величини відрізка прямої [АВ], який не паралельний ні одній з площин проекцій, методом обертання навколо осі І, перпендикулярної до П1.
Для цього проводиться вісь І через точку А перпендикулярно до П1 (А2 І2 І1 А1). Через точку В2 паралельно П1 проводиться горизонтальна площина α (В2 α2 || OX). Перетин фронтального сліду площини α2 з віссю І2 визначає фронтальну проекцію О'2 центра обертання і фронтальну проекцію радіуса обертання r2 = [О'2В2], горизонтальні проекції центра обертання О'1 І1, і радіус обертання r1 = [О'1В1].
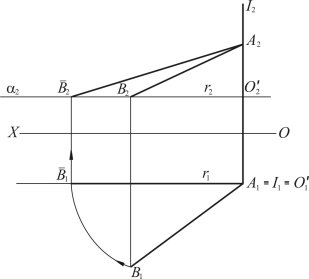
Рис 1.43
Для визначення дійсної величини відрізка [АВ] методом обертання з горизонтальної проекції центру обертання О'1 радіусом r1 горизонтальна проекція [А1В1] повертається до положення паралельного осі (OX) і займає нове положення [A1![]() 1] || (OX). Перетин перпендикуляра проведеного з
1] || (OX). Перетин перпендикуляра проведеного з ![]() до сліду α2 визначає фронтальну проекцію
до сліду α2 визначає фронтальну проекцію ![]() , поєднання проекцій А2 і
, поєднання проекцій А2 і ![]() визначає дійсну величину відрізка [АВ] методом обертання
визначає дійсну величину відрізка [АВ] методом обертання ![]() .
.
Нижче наводиться алгоритм обертання точки А навколо осі перпендикулярної до П1:
1. І П1;
2. А І (ОХ) ![]() А2 І2 (ОХ);
А2 І2 (ОХ);
3. В α || (ОX) ![]() В2 α 2 || (ОX);
В2 α 2 || (ОX);
4. α 2 ∩ І2 = О'2 — фронтальна проекція центра обертання;
5. [В2О'2] — r2 — фронтальна проекція радіуса обертання;
6. О'1 — горизонтальна проекція центра обертання;
7. r1 — горизонтальна проекція радіуса обертання;
1.4.3. Суміщення
Обертання геометричних фігур навколо осей, що належать площинам проекцій, є особливим випадком способу обертання навколо осей, паралельних площинам проекцій, і являє собою обертання площини навколо одного із її слідів до суміщення з площиною проекцій. Під час суміщення площини α загального положення з площиною проекцій люба плоска фігура, що належить цій площині α, відображається на площину проекцій (у суміщеному вигляді) у натуральну величину. У суміщеному з площиною проекції вигляді будь-яка плоска фігура зберігає свої метричні властивості (лінійні та кутові розміри), тому цей спосіб може бути використано для визначення форми і розміру фігур, розташованих у площинах, заданих слідами.
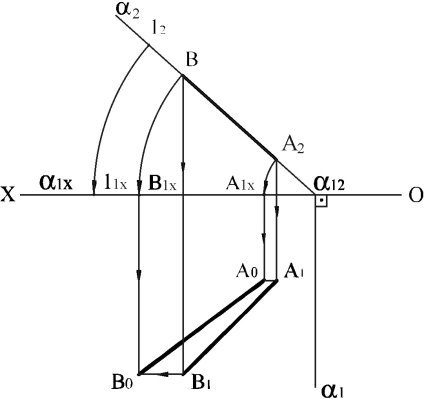
Рис. 1.44
Суміщенням називається обертання геометричної фігури навколо сліду площини. На рис. 1.44 показано суміщення фронтально-проектувальної площини α, до якої належить відрізок [АВ], з площиною П1. Для визначення дійсної величини відрізка [АВ] суміщенням з площиною П1 потрібно спочатку сумістити площину α з площиною П1, потім визначити кінці відрізка в суміщеному положенні. Для суміщення площини α з площиною П1 на α2 вибирається проекція 12, яка суміщається з горизонтальною площиною проекцій П1. Коли 12 суміститься з площиною П1, слід α2 суміститься з віссю (OX) разом з відрізком [А1xВ1x]. З точок А1x і В1x проводяться перпендикуляри до осі (OX). Одночасно з горизонтальних проекцій А1 і В1 проводяться лінії, паралельні осі (OX). Перетин горизонтальних ліній і перпендикулярів визначає відрізок |А0В0| в суміщеному положенні, який дорівнює дійсній величині відрізка [АВ], [А0В0] = |АВ|.
1.4.4. Метод заміни площин проекцій
Розглянуті вище методи перетворення ортогональних проекцій (обертання і суміщення) були пов’язані з переміщенням геометричних фігур у просторі відносно заданих площин проекцій.
Розглянемо ще один метод, такий як заміна площин проекцій, що використовується для визначення дійсної величини геометричної фігури. Особливість заміни площин проекцій у тому, що геометрична фігура залишається на своєму попередньому місці, а заміняється існуюча площина проекцій на нову так, щоб геометрична фігура стала паралельною до неї. Нові площини проекцій повинні бути перпендикулярними до існуючих. В окремих випадках потрібно заміняти дві площини проекцій. Така заміна виконується послідовно: спочатку замінюється одна площина проекцій, а потім інша. На рис. 1.45 показано просторову модель, на якій показано заміну площини П2 на площину П4. Із просторової моделі видно, що площина П4 перетинає площину П1 по лінії (О1X1). При проектуванні точки А на площину П2 і П4 видно, що [АА1] = [А2Аx] = [А4Аx4].
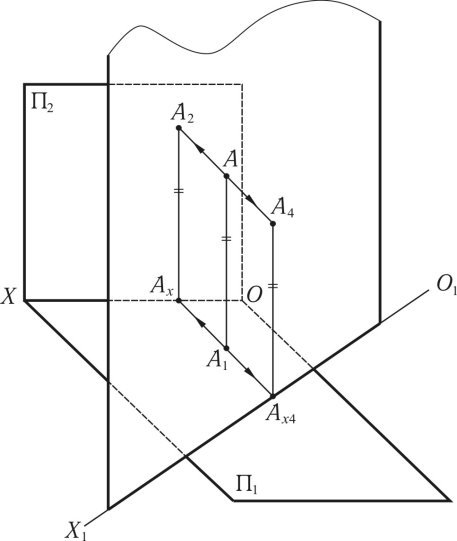
Рис 1.45
На рис. 1.46, показано заміну площини проекцій ![]() на кресленні. При заміні площини П2 на П4 утворюється нова вісь (О1X1). Фронтальна проекція А4 в новій системі площин проекцій знаходиться на відстані [А2Аx] від осі (О1X1) [А4Аx4] = [А2Аx].
на кресленні. При заміні площини П2 на П4 утворюється нова вісь (О1X1). Фронтальна проекція А4 в новій системі площин проекцій знаходиться на відстані [А2Аx] від осі (О1X1) [А4Аx4] = [А2Аx].
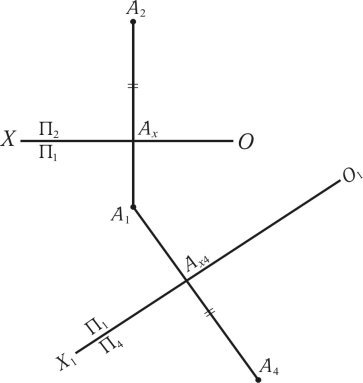
Рис 1.46
Визначення дійсної величини відрізка прямої [АВ] методом заміни площини проекцій.
При визначенні дійсної величини відрізка прямої методом заміни площин проекцій застосовується одна заміна площин проекцій ![]() яка замінюється на
яка замінюється на ![]() . На (рис. 1.47) показано визначення дійсної величини відрізка [АВ] методом заміни площин проекцій. При заміні площин П2 на П4 відбувається перехід від системи
. На (рис. 1.47) показано визначення дійсної величини відрізка [АВ] методом заміни площин проекцій. При заміні площин П2 на П4 відбувається перехід від системи ![]() до
до ![]() , площина П4 вибирається так, щоб вона була паралельна [АВ]. У такому випадку вісь (О1X1) повинна бути паралельною [А1В1]. З проекцій А1 і В1 до осі (О1X1) проводяться перпендикуляри. На продовженні перпендикулярів від осі (О1X1) відкладаються відрізки [А4Аx1] = [А2Аx] і [В4Вx1] = [В2Вx], які визначають проекції А4 і В4 на площині П4, поєднання проекцій А4 і В4 визначає дійсну величину відрізка прямої [А4В4] = |АВ|, отриманого методом заміни площин проекцій. Побудови видно з креслення (рис. 1.47).
, площина П4 вибирається так, щоб вона була паралельна [АВ]. У такому випадку вісь (О1X1) повинна бути паралельною [А1В1]. З проекцій А1 і В1 до осі (О1X1) проводяться перпендикуляри. На продовженні перпендикулярів від осі (О1X1) відкладаються відрізки [А4Аx1] = [А2Аx] і [В4Вx1] = [В2Вx], які визначають проекції А4 і В4 на площині П4, поєднання проекцій А4 і В4 визначає дійсну величину відрізка прямої [А4В4] = |АВ|, отриманого методом заміни площин проекцій. Побудови видно з креслення (рис. 1.47).
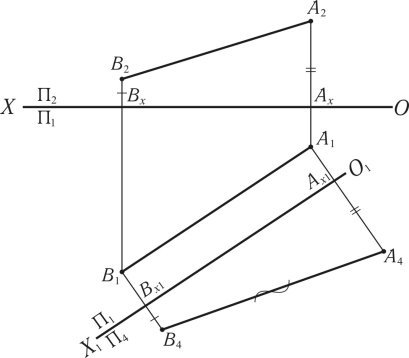
Рис. 1.47
1.4.5. Визначення відстані між двома паралельними прямими
На практиці часто потрібно вирішувати метричні задачі, до яких відносяться задачі на визначення відстані між точкою і прямою лінією, точкою і площиною, двома паралельними лініями, де доцільно застосовувати дві заміни площин проекцій.
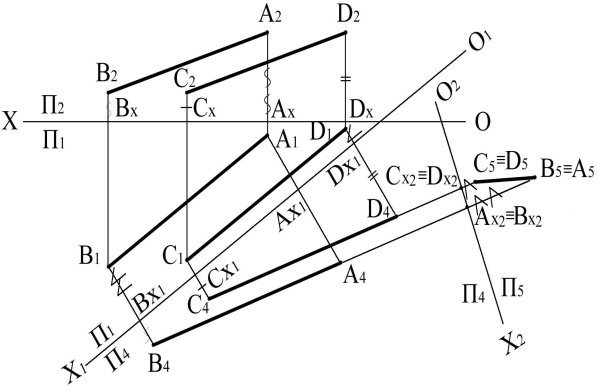
Рис. 1.48
Для визначення відстані між двома паралельними прямими потрібно виконати дві заміни площин проекцій (рис. 1.48). Першою заміною площини П2 заміняється на П4. При такій заміні прямі лінії загального положення перетворюються на прямі особливого положення. Другою заміною площини П1 на площину П5 лінії перетворюються на проектувальні. При заміні площини П2 на П4 ![]() проводиться вісь (О1X1) паралельно [(В1А1)(С1D1)]. Від осі (О1X1) з точок Вx1, Аx1, Сx1, Dx1 відкладаються відрізки [Аx1А4]=[А2Аx]; [Вx1В4]=[В2Вx]; [Сx1С4] = = [С2Сx]; [Dx1D4] = [D2Dx], які визначають положення проекцій відрізків [А4В4] і [С4D4] — в новій системі площин проекцій. При заміні П1 на П5
проводиться вісь (О1X1) паралельно [(В1А1)(С1D1)]. Від осі (О1X1) з точок Вx1, Аx1, Сx1, Dx1 відкладаються відрізки [Аx1А4]=[А2Аx]; [Вx1В4]=[В2Вx]; [Сx1С4] = = [С2Сx]; [Dx1D4] = [D2Dx], які визначають положення проекцій відрізків [А4В4] і [С4D4] — в новій системі площин проекцій. При заміні П1 на П5 ![]() проводиться вісь (О2X2) перпендикулярно до [С4D4][В4А4], від осі (О2X2) проводяться перпендикуляри, на яких відкладаються відрізки [Аx2А5]=[А1Аx1]; [Вx2В5]=[В1Вx1]; [Сx2С5]=[С1Сx1]; [Dx2D5]=[D1Dx1]. |С5D5||А5B5| — найкоротша відстань між двома паралельними прямими, отримана двома замінами площин проекцій.
проводиться вісь (О2X2) перпендикулярно до [С4D4][В4А4], від осі (О2X2) проводяться перпендикуляри, на яких відкладаються відрізки [Аx2А5]=[А1Аx1]; [Вx2В5]=[В1Вx1]; [Сx2С5]=[С1Сx1]; [Dx2D5]=[D1Dx1]. |С5D5||А5B5| — найкоротша відстань між двома паралельними прямими, отримана двома замінами площин проекцій.
Запитання для самоперевірки знань
1. Які існують способи перетворення проекцій в нарисній геометрії?
2. У чому полягає суть метода заміни площин проекцій?
3. У чому полягає суть метода обертання?
4. У чому полягає суть метода суміщення?
5. Як визначити дійсну величину відрізка прямої методом обертання?
6. Скільки замін площин проекцій треба зробити, щоб відрізок прямої загального положення спроектувати в точку?
Завдання для самоперевірки
Задача № 1
Визначити дійсну величину прямої (АВ) методом обертання.
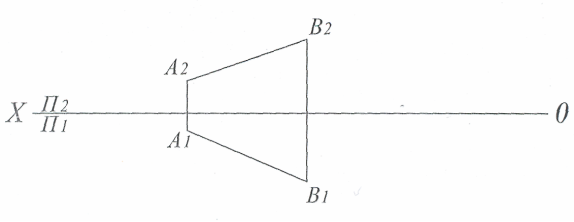
Задача № 2
Визначити дійсну величину прямої (АВ) методом суміщення.
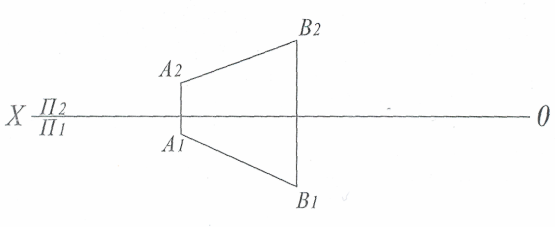
Задача № 3
Визначити дійсну величину прямої (АВ) методом заміни площин проекцій.
1.5. БАГАТОГРАННИКИ
1.5.1. Загальні характеристики багатогранників.
1.5.2.Побудова лінії перетину багатогранника площинами особливого положення.
1.5.3. Побудова точки перетину багатогранника прямою лінією.
1.5.4. Побудова лінії перетину двох багатогранників.
1.5.1. Загальні характеристики багатогранників
Багатогранною поверхнею, або багатогранником, називають поверхню, складену з кінцевого числа плоских багатокутників, що не лежать в одній площині і прилягають один до одного. Ці багатокутники називають гранями поверхні, а їхні сторони – ребрами. Багатогранні поверхні бувають замкненими і незамкненими. Найбільш поширені багатогранники – призми і піраміди.
Пірамідою називають багатогранник у якого всі грані крім однієї, мають спільну вершину, яка є вершиною піраміди. Оскільки всі грані піраміди – трикутники, піраміда визначається завданням її основи і вершини.
Призма – це багатогранник обмежений призматичною поверхнею та двома паралельними площинами, в яких лежать основи призми, грані призматичної поверхні називаються гранями призми, а її ребра – ребрами призми. Основами призми є рівні багатокутники, а бічні ребра дорівнюють одне одному. Коли основи призми не паралельні між собою, вона зветься зрізаною. Якщо ребра призми перпендикулярні до її основи, призму називають прямою, коли ця умова не витримується, - похилою.
Призми та піраміди розрізняють за числом вершин основи. У випадку, коли основою піраміди чи призми є правильний багатокутник, а висота збігається з віссю, піраміду та призму називають правильною.
На кресленні багатогранники задаються ребрами та вершинами.
1.5.2.Побудова лінії перетину багатогранника площинами
особливого положення.
Задача 1. Побудова лінії перетину тригранної піраміди фронтально-проектувальною площиною.
Для побудови лінії перетину тригранної піраміди SABC площиною застосовується метод побудови точки перетину прямої лінії з площиною. Така побудова в просторі показана на рис. 1.49.
SABC ∩ = 1,2,3.
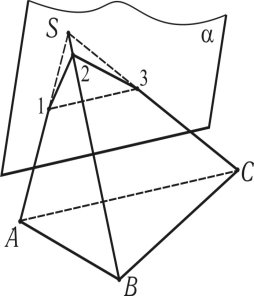
Рис. 1.49
Побудова лінії перетину тригранної піраміди
фронтально-проектувальною площиною на кресленні показано на рис. 1.50. Піраміда своєю основою знаходиться на площині П1. Спочатку виконується горизонтальна проекція S1A1B1C1, потім фронтальна S2A2B2C2 за допомогою ліній проектувального зв’язку.
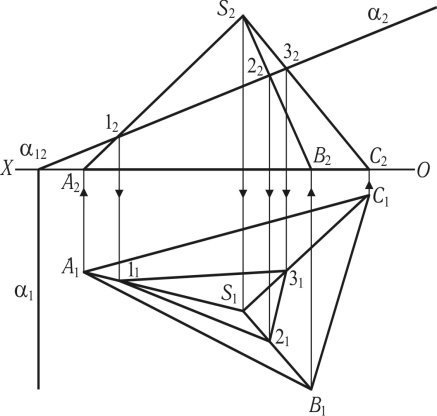
Рис. 1.50
Піраміду перетинає фронтально-проектувальна площина α. Фронтальний слід площини α2, горизонтальний α1. Площина α особливого положення, вона має збиральні властивості, тому фронтальна проекція лінії перетину (α ∩ SABC) збігається з фронтальним слідом площини (α2 122232). Горизонтальна проекція лінії перетину визначається за допомогою ліній проектувального зв’язку (11, 21, 31).
Задача 2. Побудова лінії перетину призми профільно-проектувальною площиною.
Для побудови лінії перетину призми профільно-проектувальною площиною (рис. 1.51) спочатку виконуються три проекції тригранної призми (BB'AA'CC'), після чого проводиться фронтальний 2 і 1 горизонтальний слід. По точках збігу слідів 23 і 13 і '13 виконується профільний слід площини 3, який визначає профільну проекцію ліній перетину (13,23,33,43).
Внаслідок того, що площина — особливого положення, то профільна проекція лінії перетину 13,23,33,43 збігається з профільним слідом площини 3. Фронтальні і горизонтальні проекції точок перетину визначаються за допомогою ліній проектувального зв’язку.
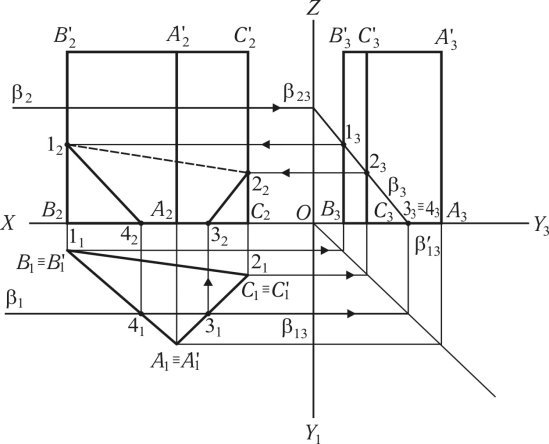
Рис. 1.51
Побудови лінії перетину видно з креслення та алгоритму розв’язання задачі:
(AA'BВ'CС’) ∩ П3 = (1,2,3,4);
3 ∩ (B3B'3С3C'3) = 13,23,33,43 3.
Фронтальні та горизонтальні проекції (12223242) (11213141) визначаються за допомогою ліній проектувального зв’язку.
1.5.3. Побудова точки перетину багатогранника прямою лінією.
Побудову точки перетину багатогранника прямою лінією розглянемо на прикладі трьох задач.
Задача 1. Побудова точки перетину тригранної піраміди прямою лінією.
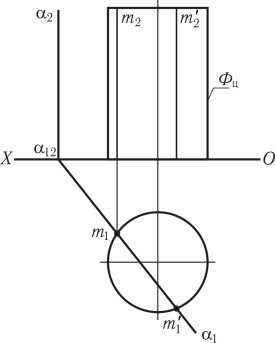
Побудову точки перетину багатогранника SABC прямою лінією m наведено на рис. 1.52. Піраміда своєю основою знаходиться на площині П1, A1B1C1 П1 m ∩ SABC = К K'.
Для побудови точки перетину піраміди SABC прямою лінією m (m2, m1) потрібно пряму m залучити в площину α, знайти лінію перетину площини з багатогранником. Перетин відповідних проекцій лінії перетину з проекцією лінії, визначає проекції точок перетину прямої з багатогранником. Проекції точок перетину на другій площині проекцій визначаються за допомогою ліній проектувального зв’язку. В даному випадку доцільно пряму m залучити у фронтально-проектувальну площину α П2, тоді m2 α2. Після чого визначається лінія перетину SABC ∩ α.
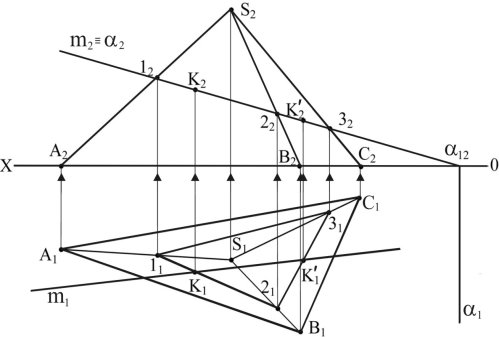
Рис. 1.52
Фронтальна проекція лінії перетину α2 ∩ S2A2B2C2 = (122232) збігається зі слідом площини, горизонтальна проекція визначається за допомогою ліній проектувального зв’язку. Перетин горизонтальної проекції лінії перетину з горизонтальною проекцією лінії (112131) ∩ m1 = ![]() визначає горизонтальні проекції точок перетину багатогранника прямою лінією. Фронтальні проекції (
визначає горизонтальні проекції точок перетину багатогранника прямою лінією. Фронтальні проекції (![]() ) визначаються за допомогою ліній проектувального зв’язку.
) визначаються за допомогою ліній проектувального зв’язку.
Задача 2. Побудова точки перетину тригранної піраміди прямою лінією особливого положення.
Побудова перетину піраміди прямою лінією особливого положення виконується за схемою:
1. Залучається лінія в площину особливого положення;
2.Визначається лінія перетину багатогранника з площиною;
3.Визначаються проекції точок перетину відповідних проекцій лінії з відповідними проекціями лінії перетину.
Останні є проекціями точок перетину, протилежні проекції визначаються за допомогою ліній проектувального зв’язку.
На рис. 1.53 показано побудову точок перетину горизонтально проектувальною прямою лінією m з тригранною пірамідою SABC. Побудови видно з креслення та алгоритму розв’язання задачі: m П1 m1 1; 1 ∩ S1A1B1C1 = (11;21;31) — горизонтальна проекція лінії перетину, яка збігається зі слідом площини, фронтальна проекція лінії (122232) — визначається за допомогою ліній проектувального зв’язку. Перетин (1222) ∩ m2 = K2 — фронтальна проекція точки перетину m ∩ SABC. Горизонтальна проекція K1 визначається за допомогою проектувального зв’язку m ∩ ABC = m1 ![]() m2 ∩ A2B2C2 = m 2 — фронтальна проекція точки перетину піраміди SABC лінією m. K2, n΄2 — фронтальні проекції точок перетину піраміди SABC прямою m, K1, m1 n΄1 — горизонтальні проекції.
m2 ∩ A2B2C2 = m 2 — фронтальна проекція точки перетину піраміди SABC лінією m. K2, n΄2 — фронтальні проекції точок перетину піраміди SABC прямою m, K1, m1 n΄1 — горизонтальні проекції.
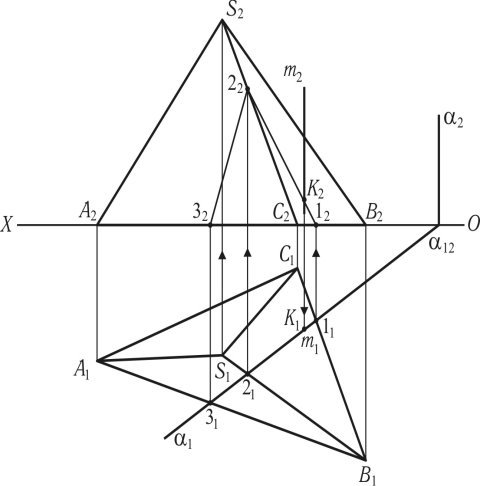
Рис. 1.53
Задача 3. Побудова точок перетину прямої лінії загального положення з проектувальною призмою.
Принцип побудови точок перетину призми з прямою відповідає загальній схемі побудови точок перетину багатогранника з прямою лінією.
На рис. 1.54 наведено побудову точок перетину лінії загального положення m з тригранною призмою AA'BB'CC'. Побудови видно з креслення та алгоритму розв’язання задачі. Слід визначити, що на кресленні тригранна призма (AA΄ BB΄ CC΄) представлена у вигляді фронтальної і горизонтальної проекцій, m2 – фронтальна проекція прямої, m1 – горизонтальна проекція прямої.
Спочатку m залучається в горизонтально-проектувальну площину , m1 1. Площина перетинає призму AA'BB'CC' по фігурі прямокутника nn'n''n''' .
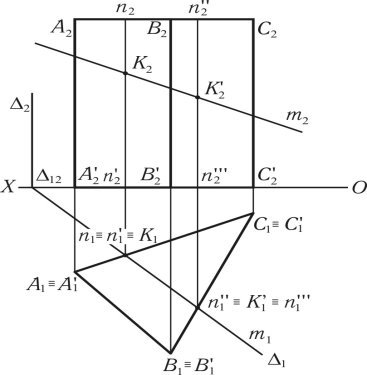
Рис. 1.54
Перетин фронтальної проекції ![]() з m2 визначає фронтальні проекції K2 і
з m2 визначає фронтальні проекції K2 і ![]() точок перетину лінією m призми AA'BВ'СC'. Горизонтальні проекції визначаються за допомогою ліній проектувального зв’язку.
точок перетину лінією m призми AA'BВ'СC'. Горизонтальні проекції визначаються за допомогою ліній проектувального зв’язку.
1. m П1 ^ m1 1;
2. ![]() ∩( AA'BB'CC') = ( nn'n''n''' );
∩( AA'BB'CC') = ( nn'n''n''' );
3. m2∩(![]() ) = К2
) = К2 ![]() — фронтальні проекції точок перетину, К1
— фронтальні проекції точок перетину, К1 ![]() — горизонтальні проекції точок перетину. m ∩ (AA'BВ'СC’).
— горизонтальні проекції точок перетину. m ∩ (AA'BВ'СC’).
1.5.4 . Побудова лінії перетину двох багатогранників
При побудові ліній перетину двох багатогранників застосовується метод визначення точок перетину прямої з площиною. Ламана лінія, що з’єднує у певному порядку ці точки і визначить лінію перетину багатогранників.
Розглядається перетин двох призм (AА';ВВ';СС') і (МM';NN';GG') які представлені на кресленні у вигляді проекцій, одна з яких направлена перпендикулярно до горизонтальної площини проекцій, а друга — під нахилом (рис 1.55). Для побудови лінії перетину таких призм виконується горизонтальна і фронтальна проекції вертикальної тригранної призми. Після чого виконується похила призма. Горизонтальна проекція (M1'M1;G1'G1’;N1'N1) паралельна осі (ОХ). Фронтальна проекція (М2'М2;N2'N2;G2'G2) знаходиться під довільним кутом до осі (ОХ).
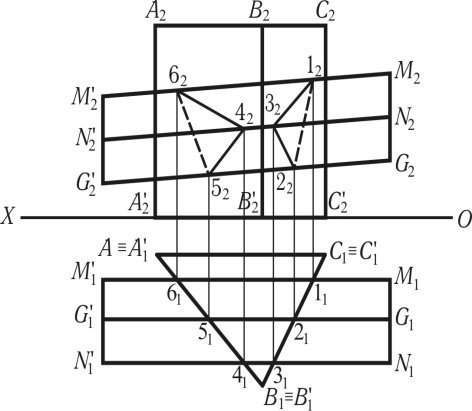
Рис. 1.55
У зв’язку з тим, що призма перпендикулярна до горизонтальної площини проекцій, то її грані є горизонтально-проектувальними площинами, які мають збиральні властивості, тому горизонтальні проекції лінії перетину похилого багатогранника збігаються з горизонтальною проекцією грані ![]() і грані
і грані ![]() . Горизонтальна проекція лінії перетину (112131) і (415161), фронтальні проекція (122232) і (425262), отримані за допомогою ліній проектувального зв’язку. Поєднання фронтальних проекцій точок визначає фронтальні проекції лінії перетину.
. Горизонтальна проекція лінії перетину (112131) і (415161), фронтальні проекція (122232) і (425262), отримані за допомогою ліній проектувального зв’язку. Поєднання фронтальних проекцій точок визначає фронтальні проекції лінії перетину.
Запитання для самоперевірки знань
1. Який отримаємо багатогранник, якщо сполучимо ребрами центри граней куба?
2. Які плоскі фігури можуть утворитися при перетині тетраедра площиною?
3. Коли ділянка лінії перетину двох багатогранників буде видимою?
Завдання для самоперевірки
Задача № 1
Побудувати лінію перетину багатогранника площиною. 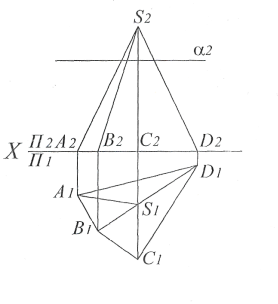
Задача № 2
Побудувати лінію перетину багатогранника площиною.

1.6. РОЗГОРТКА БАГАТОГРАННИКІВ
1.6.1. Загальні характеристики розгорток багатогранників.
1.6.2. Розгортка піраміди методом трикутника.
1.6.3. Розгортка призм методом розкатки.
1.6.4. Розгортка призми довільного розташування методом нормального перерізу.
1.6.1. Загальні характеристики розгорток багатогранників
Розгортка поверхні об’ємного предмета – це плоска фігура, що утворюється, коли поверхню розрізати вздовж якоїсь лінії і сумістити з площиною креслення.
Розгортка поверхні многогранника є плоскою фігурою, утвореною при суміщені з площиною креслення всіх граней многогранника у відповідності їх розташування на многограннику. Тому і побудова розгортки поверхні многогранника полягає в послідовній побудові всіх його граней.
Розгортки геометричних фігур призначені для визначення площини матеріалу, потрібного для виготовлення виробу. Наприклад, потрібно з листа жерсті зробити лійку чи трубу або підготувати матеріал для обшивки корпуса пароплава. Така робота потребує знання дійсної величини поверхні виробу. У всіх випадках можна отримати поверхню виробу методом трикутника.
Розглянемо побудову розгорток пірамід і призм як найбільш поширених в інженерній практиці багатогранників. Для розгортки похилої призми загального положення застосовується метод нормального перерізу, для розгортки призми особливого положення – метод розкатки.
Побудований зовнішній контур розгортки обводять суцільно товстою основною лінією, а лінію згину – штих пунктирною з двома крапками.
1.6.2. Розгортка піраміди методом трикутника
Розгортки методом трикутника можна застосовувати у всіх випадках побудови розгорток, але доцільно його застосовувати при побудові розгортки піраміди.
При розгортці піраміди потрібно спочатку визначити дійсну величину ребер, а потім виконувати креслення розгортки.
На рис. 1.56 розглядається приклад розгортки тригранної піраміди ABCS. Основа піраміди розташована на площині П1.
З креслення видно, що ребро SA займає особливе положення, а тому[S2A2] проектується на фронтальну площину проекцій у дійсну величину. Для того щоб побудувати розгортку, потрібно визначити дійсну величину ребер [SC] і [SB]. Відомо три методи визначення дійсної величини геометричних фігур: метод прямокутного трикутника, метод обертання і метод заміни площин проекцій. Вибирається метод, де найменше геометричних побудов. У даному випадку це буде метод обертання.
При визначенні дійсної величини ребер методом обертання проводиться вісь перпендикулярно до площини П1 через вершину піраміди S J П1 S J S2 J2 S1 J1. Для визначення основних параметрів обертання проводиться площина , 1 ≡ 2 через вісь.
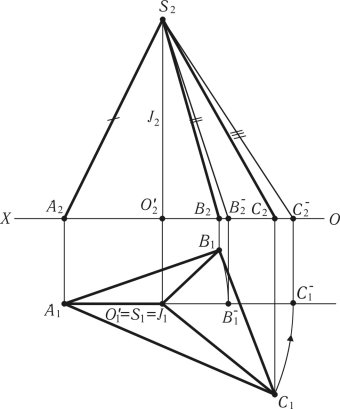
Рис. 1.56
З горизонтальної проекції центра обертання О1, який збігається з горизонтальною проекцією вершини S1, повертаються горизонтальні проекції ребер до положення, паралельного осі (ОХ) ![]() ║(ОХ) і
║(ОХ) і ![]() ║(ОХ).
║(ОХ).
Фронтальні проекції ![]() і
і ![]() проектуються на вісь (ОХ). З’єднання відповідних проекцій
проектуються на вісь (ОХ). З’єднання відповідних проекцій ![]() і
і ![]() визначає дійсну величину ребер
визначає дійсну величину ребер ![]() = |SB| і
= |SB| і ![]() = |SC|.
= |SC|.
Після визначення дійсної величини ребер виконується розгортка піраміди методом трикутника (рис. 1.57), для чого вибирається в будь-якому місці форматного листа паперу точка S0, з якої проводиться під довільним кутом ребро S0А0 = |S2А2|. З кінця ребра S0А0 радіусом А1В1 проводиться дуга, крім того, проводиться дуга з вершини S0 радіусом ![]() . Перетин дуг визначає точку В0, з’єднання кінців ребер А0, В0 і S0 визначає поверхню грані, яка сумістилася з площиною. Так виконується розгортка всіх граней. Це видно з креслення S0В0С0А0. Після чого добудовується основа.
. Перетин дуг визначає точку В0, з’єднання кінців ребер А0, В0 і S0 визначає поверхню грані, яка сумістилася з площиною. Так виконується розгортка всіх граней. Це видно з креслення S0В0С0А0. Після чого добудовується основа.
Для добудови основи піраміди з точки С0 радіусом С0А0 та з точки В0 радіусом В0А0 проводяться дуги. Перетин дуг визначає точку А0. З’єднання А0В0С0 визначає основу в суміщеному положенні.
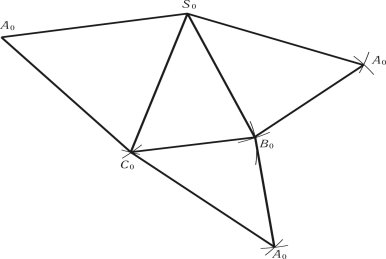
Рис. 1.57
1.6.3. Розгортка призм методом розкатки
Розглянемо цей метод на прикладі розгортки похилої та проектувальної призм.
Розгортка похилої призми методом розкатки.
Розгортка методом розкатки застосовується у випадку, коли призма розташована паралельно до однієї з площин проекцій.
На (рис. 1.58) зображено побудову розгортки призми АВСА'В'С', ребра якої паралельні площині П2. На кресленні призма представлена фронтальною та горизонтальною проекціями.
При побудові розгортки методом розкатки вибирається ребро АА', навколо якого обертаються грані до суміщення з площиною, паралельною площині П2.
Для цього з фронтальної проекції В2 проводиться перпендикуляр до фронтальної проекції ребра А2А'2. На перпендикулярі виконується насічка дугою, проведеною з А2 радіусом, рівним А1В1. Перетин дуги з перпендикуляром визначає точку В0, яка знаходиться в площині, паралельній площині П2. А2 з’єднують з В0.
Для визначення В'0 проводиться лінія В0В'0, паралельна фронтальній проекції ребра А2А'2, з А'2 проводиться лінія А'2В'0, паралельна А2В0, перетин А'2В'0 з В0В'0 визначає В'0. З’єднання отриманих точок А2А'2 В0В'0 визначає грань піраміди АВСА'В'С' в суміщеному положенні.
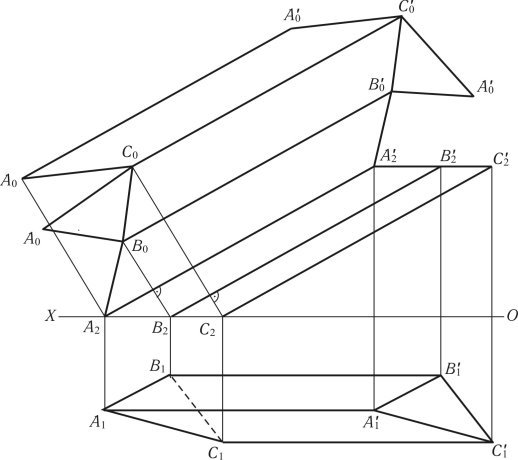
Рис. 1.58
Для визначення в суміщеному положенні точки С потрібно з С2 провести перпендикуляр до ребра В2В'2, радіусом В0С0 = В1С1, провести дугу, перетин дуги з перпендикуляром визначає положення С0. З С0 проводиться лінія, паралельна В0В'0, з точки В'0 проводиться лінія В'0С'0 паралельно В0С0, перетин С0С'0 з В'0С'0 визначає С'0 в суміщеному положенні.
Для добудови верхньої і нижньої основ призми, до бокової розгортки з точок В0 і В'0 проводяться дуги радіусами В'0А'2 і В0А2, а також з С0 і С'0 радіусами С0А0 і С'0А'0, перетин яких визначає положення точок А0 і А'0 в суміщеному положенні. В0С0А0 — нижня основа призми в суміщеному положенні, В'0С'0А'0 — верхня основа призми в суміщеному положенні з площиною, паралельною площині П2.
Розгортка проектувальної призми методом розкатки.
Проектувальна призма на рис. 1.59 представлена в вигляді фронтальної і горизонтальної проекції. Вона своєю основою знаходиться на площині П1, ребра основи такої призми СА; АВ і ВС проектуються на П1 у дійсну величину і дорівнюють СА = С1А1; АВ = А1В1; ВС = В1С1. Ребра [С2С'2, В2В'2 і А2А'2 проектуються на фронтальну площину проекцій у дійсну величину. Для побудови розгортки призми (рис. 1.60) проводиться горизонтальна лінія (ОХ), на якій відкладаються дійсні величини ребер основи С1В1, В1А1 і А1С1, з точок С1; В1; А1 і С1 ставляться перпендикуляри до осі OX рівні висоті ребер призми С2С'2; В2В'2; А2А'2, які визначають точки С'2; В'2; А'2 і С'2.
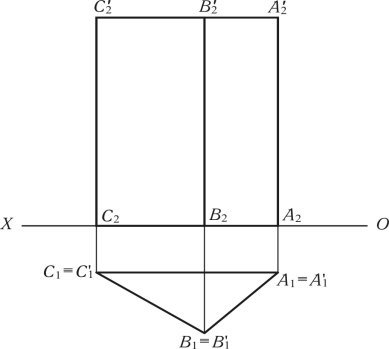
Рис. 1.59
Поєднання точок С2С'2; В2В'2; А2А'2 і С1С'1 визначає бічну поверхню призми, отриману методом розкатки. Добудова основи до бокової поверхні призми виконується за допомогою двох дуг, виконаних радіусами B2С2 ∩ A2С2 = С2. Добудова верхньої основи виконується аналогічно.
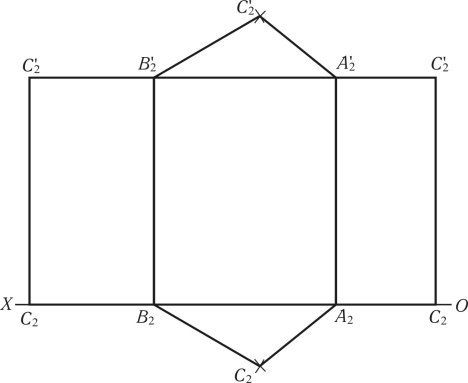
Рис. 1.60
1.6.4. Розгортка призми довільного розташування методом
нормального перерізу
Метод нормального перерізу застосовується для розгортки призми довільного розташування відносно площин проекцій (рис. 1.61).
Нормальним перерізом призми називається її переріз площиною, яка перпендикулярна ребрам призми. Така площина перетинає призму по деякому багатограннику, сторони якого перпендикулярні ребрам призми і дорівнюють відстаням між відповідними сусідніми ребрами призми.
Для здійснення розгортки методом нормального перерізу спочатку визначається дійсна величина ребер методом заміни площин проекцій, потім дійсна величина нормального перерізу, для чого проводиться площина особливого положення ![]() 4 перпендикулярно до П4 і ребер. Визначається дійсна величина нормального перерізу. Коли відома дійсна величина ребер і нормального перерізу, виконується розгортка (рис. 1.62).
4 перпендикулярно до П4 і ребер. Визначається дійсна величина нормального перерізу. Коли відома дійсна величина ребер і нормального перерізу, виконується розгортка (рис. 1.62).
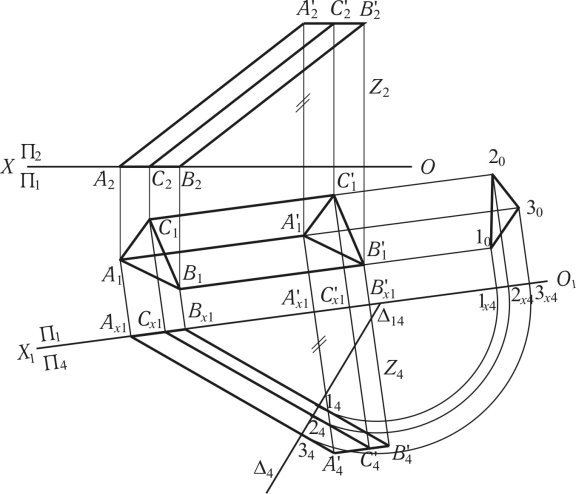
Рис. 1.61
Розгортка тригранної призми АА'ВВ'СС' методом нормального перерізу наведена на рис. 1.61 і рис. 1.62. Побудова розгортки складається з трьох складових: визначення дійсної величини ребер призми, побудова дійсної величини нормального перерізу і побудова розгортки. Слід визначити що призма представлена в вигляді креслень на відповідних площинах проекцій.
Для визначення дійсної величини ребер призми АА'ВВ'СС' доцільно застосувати метод заміни площин проекцій — перейти від системи площин проекцій П1/П2 до системи П1/П4, П4 проведена паралельно ребрам призми. В такому випадку (О1Х1) слід провести паралельно горизонтальним проекціям ребер С1С'1; А1А'1; В1В'1. Горизонтальна проекція основи призми А1В1С1 проектується на вісь (О1Х1) в вигляді Ах1Вх1Сх1. Горизонтальна проекція А'1В'1С'1 проектується в точки А'4В'4С'4, які знаходяться на відстані Z від осі (О1Х1), Ах1А'4; Сх1С'4; Вх1В'4; є дійсні величини ребер призми.
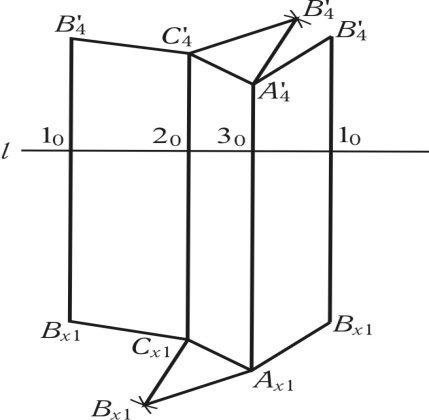
Рис. 1.62
Для визначення дійсної величини нормального перерізу проводиться фронтально-проектувальна площина перпендикулярно до дійсної величини ребер піраміди 4 {Ах1А'4; Сх1С'4; Вх1В'4}. Фронтальна проекція лінії перетину збігається з слідом площини (142434) 4. Дійсна величина нормального перерізу визначається при суміщені 4 з площиною П1. У суміщеному положенні 4 збігається з віссю (О1Х1), фронтальна проекція лінії перерізу (14; 24; 34) також збігається з віссю (О1Х1). Перетин перпендикулярів, проведених з 1х42х43х4 до осі (О1Х1), з продовженнями горизонтальних проекцій ребер А1А'1; В1В'1; С1С'1 визначають точки 102030, поєднання яких визначає дійсну величину лінії нормального перерізу.
Побудова розгортки призми починається з проведення лінії l, на якій відкладаються відрізки сторін нормального перерізу 1020; 2030; 3010 через кінці яких проводяться вертикальні лінії в обидві сторони від лінії l; відрізки беруться з рис. 6.6. Вниз відкладаються 10Bх1 = 14Bх1; 20Cх1 = 24Cх1; 30Ах1 = 34Ах1; 10Bх1= = 14Bх1, вгору відкладаються відрізки 10B'4 = 14B'4; 20C'4 = 24C'4; 30А'4 = 34А'4; 10B'4 = = 14B'4, поєднання точок В'4, Вх1, С'4, Сх1, А'4, Ах1, B'4, Bх1 — визначає бокову поверхню призми. Для побудови повної поверхні призми до бокової поверхні добудовуються верхня і нижня основи. Добудова верхньої основи призми до бокової поверхні починається з проведення дуг, з А'4 радіусом А'4B'4 і радіусом C'4B'4, перетин дуг визначає положення точки B'4 поєднання якої з C'4 і А'4 визначає поєднання верхньої основи призми з боковою. Аналогічно добудовується нижня основа, перетин дуг, проведених з Aх1 радіусом Aх1Bх1 і з Cх1 радіусом Cх1Bх1, визначає Bх1. Поєднання Вх1Сх1Ах1 визначає нижню основу призми.
Запитання для самоперевірки знань
1. Які методи розгортки застосовуються у нарисній геометрії?
2. Розгортка яких багатогранників будується методом трикутника?
3.Розгортка якого багатогранника будується методом нормального перерізу?
4. Розгортка яких багатогранників будується методом розкатки?
5. Якою лінією вказують місця згину на розгортках?
Завдання для самоперевірки
Задача №1.
Побудуйте розгортку поверхні паралелепіпеда з прямокутною основою розміром 45х30 мм і висотою 25 мм.
Задача №2.
Побудуйте розгортку поверхні тригранної призми зі стороною основи 25 мм і висотою 40 мм.
Задача №3.
Побудуйте розгортку поверхні трикутної піраміди зі стороною основи 30 мм і довжиною бічного ребра 50 мм.
1.7. КРИВІ ЛІНІЇ
1.7.1. Загальні характеристики кривих ліній.
1.7.2. Визначення типу кривої лінії.
1.7.3. Визначення радіуса кривини кривої лінії методом кола.
1.7.4. Побудова гвинтової лінії.
1.7.1. Загальні характеристики кривих ліній
Криві лінії широко використовують в різних галузях техніки і будівництва. Це траєкторія переміщення різноманітних об’єктів, обриси інженерних конструкцій та архітектурних споруд. Перетин поверхонь, графічне уявлення складних функціональних процесів. Вони можуть бути задані рівнянням в системі координат, утворитися в результаті перетину двох поверхонь, відповідати певним залежностям. Або можуть бути задані графічно. В нарисній геометрії криві лінії вивчають за їхніми проекціями.
Крива лінія – це є траєкторія переміщення точки в просторі. Криві лінії поділяються на площинні та просторові.
Площинна крива лінія – це лінія, яка всіма своїми точками (1, 2, 3, 4, 5) збігається з площинною Р (рис. 1.63). Це широко відомі лінії: коло, еліпс, гіпербола, парабола тощо.
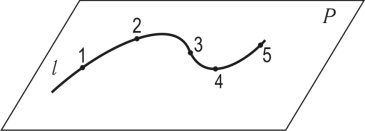
Рис. 1.63
Просторова крива лінія — це лінія, яка перетинає площину Р в декількох точках (1, 2) (рис. 1.64) і не належить площині Р. До них належать циліндрична спіраль, конічна спіраль. На відміну від площинних кривих, просторові задаються двома проекціями.
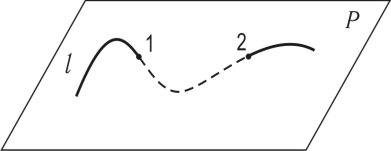
Рис. 1.64
Для побудови кривої лінії на кресленні позначаються проекції точок (12, 22, 32, … 72) (11, 21, 31, … 71), які знаходяться на лінії проекційного зв’язку (рис. 1.65).
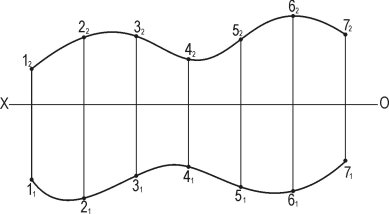
Рис. 1.65
1.7.2 . Визначення типу кривої лінії
Для визначення типу кривої лінії проводяться площина, яка задається двома прямими лініями m і n, що належать до кривої лінії (рис. 1.66). Прямі m і n (m2n2m1n1) належать до кривої лінії , так як 12; 22; 32; 42 належать до l2, а 11; 21; 31; 41 належать до l1. У таких прямих є спільна точка, в нашому випадку — це точка K (K2, K1). Така крива лінія називається площинною.
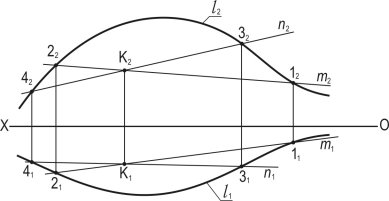
Рис. 1.66
Крива лінія, всі точки якої не належать до площини, називається просторовою.
Для визначення довжини просторової кривої лінії l (рис. 1.67), на осі ОY3 відкладаються відрізки [11-21]; [21-31]; [31-41]; [41-51]; [51-61], взяті з горизонтальної проекції прямої l1. З кінців відрізків проводяться перпендикуляри з точок 11; 21; 31; 41; 51; 61 до осі ОY3, з проекцій 12; 22; 32; 42; 52 і 62 проводяться перпендикуляри до осі OZ. Перетин відповідних перпендикулярів визначає точки, які належать до лінії l в просторі, 1; 2; 3; 4; 5; 6 — довжина лінії в просторі.
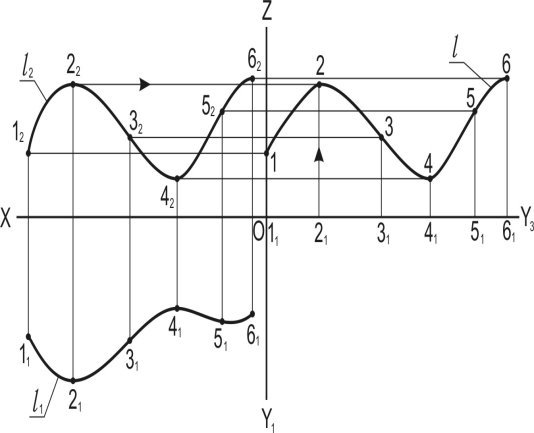
Рис. 1.67
1.7.3 . Визначення радіуса кривизни кривої лінії методом кола
Кривизну вимірюють радіусом кривизни, який є радіусом кола, проведеного через точку і дві точки, нескінченно близькі до неї по обидва боки. Кривина є оберненою до радіуса кола кривини R.
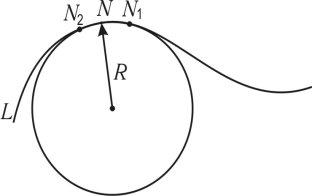
Рис. 1.68
Для визначення кривизни кривої лінії в заданій точці N на кривій L вибирається точка N, по обидва боки від якої задаються точки N1 і N2 (рис. 1.68). Через три точки (N2NN1) проводиться коло. Радіус R такого кола є радіусом кривизни кривої лінії.
1.7.4. Побудова гвинтової лінії на поверхні циліндра
Гвинтова лінія – це траєкторія руху точки по поверхні обертання.
Гвинтові лінії широко використовуються у техніці і будівництві: різьбові вироби, свердла, пружини, гвинтові сходи.
Найбільш поширена у техніці циліндрична гвинтова лінія.
Гвинтова лінія утворюється на поверхні циліндра, коли він обертається навколо осі І2, а точка, яка належить до поверхні циліндра, має прямолінійний рух. Дві точки на твірній при повному обертанні циліндра визначають крок гвинтової лінії h. Гвинтова лінія може бути правого та лівого напрямку.
За діаметр гвинтової циліндричної лінії береться діаметр циліндра, по поверхні якого переміщується точка. Шагом гвинтової лінії називають довжину частини утворюючих циліндра, на котру переміщується точка за один оберт цієї утворюючої навколо осі циліндру.
Для побудови гвинтової лінії виконуються горизонтальна і фронтальна проекції циліндра у вигляді кола і прямокутника (рис. 1.69). Висота останнього дорівнює кроку h гвинтової лінії. Вертикальна і горизонтальна проекції діляться на 12 рівних частин. З відповідних горизонтальних проекцій точок(11;21;31..) проводяться лінії зв’язку до перетину з відповідними проекціями ліній рівня (02; 12; 22; 32...). Точки перетину визначають точки, які належать гвинтовій лінії, поєднання останніх визначає фронтальну проекцію гвинтової лінії.
Для визначення видимості фронтальної проекції гвинтової лінії на горизонтальній площині проекцій проводиться лінія S зі стрілкою на кінці, проекції точок, які знаходяться ближче до стрілки, будуть видимі, ті, що знаходяться за лінією (62; 122), будуть невидимі.
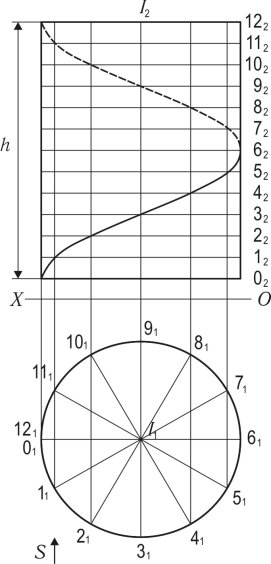
Рис. 1.69
Запитання для самоперевірки знань
1. Яка лінія називається кривою?
2. Які лінії належать до площинних кривих ліній та просторових?
3.Як визначити тип кривої лінії?
4. Яким методом визначається радіус кривизни кривої лінії?
5. Як утворюється гвинтова лінія на поверхні циліндра?
Завдання для самоперевірки
Задача №1.
Побудувати гвинтову лінію на поверхні циліндра з параметрами:
Нц ∕ Lц=2.
(Нц – висота циліндра, Lц – діаметр циліндра.)
1.8. ПОВЕРХНІ
1.8.1. Загальні характеристики виконання поверхонь.
1.8.2. Побудова лінії перетину поверхні обертання площиною особливого положення.
1.8.3. Побудова точки перетину поверхні обертання прямою лінією.
1.8.4. Побудова лінії перетину двох поверхонь обертання методом січних площин та методом січних куль.
1.8.1. Загальні характеристики виконання поверхонь
Поверхні можна розглядати як нерозривну сукупність положень лінії, що переміщується у просторі (як траєкторії руху цієї лінії).
В нарисній геометрії поверхні задаються графічно, тому треба її розглядати як сукупність послідовних положень в просторі ліній.
Існують три методи виконання поверхні: алгебричний метод F(x,y,z) = 0, де x, y, z — координати точок, каркасний метод та кінематичний метод. В нарисній геометрії застосовується кінематичний метод. Кінематичний метод має визначник Ф (Г) [A], де Г — геометрична складова, А — алгоритмічна складова.
Геометрична складова може бути у вигляді точки, лінії, поверхні, алгоритмічна складова у вигляді формули, закону.
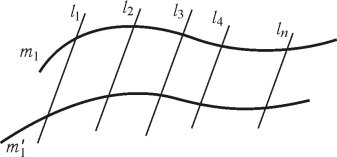
Рис. 1.70
Для побудови поверхні за допомогою кінематичного методу використовуються геометричні і алгоритмічні складові. На рис. 1.70 показана побудова поверхні двома напрямними m1, m′1 і твірною l. Переміщення твірної l по напрямним (m1, m′1) утворює поверхню. Для побудови конуса використовується напрямна вісь I, твірна l. Алгоритмічна складова пропонує переміщення твірної l по колу навколо напрямної I. Побудову конуса показано на рис. 1.71.
Рис. 1.71
1.8.2. Побудова лінії перетину поверхні обертання площиною особливого положення.
Розглянемо побудову лінії перетину обертання з трьома видами площин особливого положення.
Перетин поверхні циліндра з площиною особливого положення (горизонтально-проектувальною).
Площина при перетині поверхні обертання утворює лінію перетину. На рис. 1.72 показана побудова лінії перетину циліндра Фц горизонтально-проектувальною площиною Фц ∩ (1; 2) П1. Площина перетинає циліндр Фц по прямокутнику (mm′), твірні якого проектуються на горизонтальну площину проекцій у вигляді точок m1 і m′1, на фронтальну, у вигляді проекцій прямих ліній m2 і m′2.
Перетин поверхні циліндра з площиною особливого положення (фронтально-проектувальною).
На рис. 1.73 показано побудову лінії перетину циліндра Фц фронтально-проектувальною площиною β. Циліндр своєю основою знаходиться на площині П1, вісь якого направлена перпендикулярно до площини П1. Фронтальна проекція лінії перетину циліндра (12,22,32,42,) збігається зі слідом β2, горизонтальна проекція збігається з основою циліндра. Для побудови профільної проекції лінії перетину спочатку визначаються проекції характерних точок за допомогою ліній проектувального зв’язку: 13; 23; 33; 43, потім проміжні проекції точок 53; 63, які визначаються за допомогою площини-посередника ∆||П3.
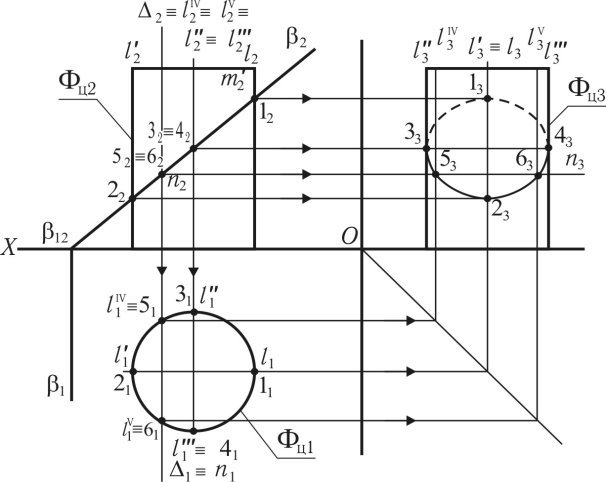
Рис. 1.73
Побудову профільної проекції лінії перетину показано на рис. 8.4, з якого видно, що 2∩2 по прямій лінії n, фронтальна проекція n2 проектується в точку, горизонтальна та профільна проекції проектуються у вигляді проекцій прямих ліній n1 і n3. Площина ∆ перетинає Фц циліндра по прямокутнику: ∆∩Фц=![]() , площину β2 по прямим лініям n2;n1;n3. Перетин
, площину β2 по прямим лініям n2;n1;n3. Перетин ![]() = 53 63 визначає профільні проекції проміжних точок. Горизонтальні та фронтальні проекції (51;61) (52;62) визначаються за допомогою ліній проектувального зв’язку. Видимість лінії перетину визначено за допомогою метода конкуруючих точок.
= 53 63 визначає профільні проекції проміжних точок. Горизонтальні та фронтальні проекції (51;61) (52;62) визначаються за допомогою ліній проектувального зв’язку. Видимість лінії перетину визначено за допомогою метода конкуруючих точок.
Побудова лінії перетину конуса площиною особливого положення
Площини особливого положення перетинають конус по колу, трикутнику, еліпсу, параболі та гіперболі в залежності від величини кута нахилу площини до осі конусу. Характерні проекції точок лінії перетину визначаються з побудови, перетину сліду площини з твірними, а також за допомогою площин-посередників. Так, на рис. 1.74 площина (2) розташована відносно осі конуса під кутом 90º. Вона перетинає фігури конуса по колу радіуса r2, яке на фронтальній площині проекцій збігається зі слідом площини 2 і проектується в пряму лінію, на горизонтальну площину проекцій проектується у вигляді кола радіусом r1=r2. При перетині конуса площиною ', направленою перпендикулярно до площини П1, яка проходить через вісь конуса і його вершину S (рис. 1.74). У такому випадку фігура конуса перетинається площиною ' по трикутнику (B'1S'1A'1) — горизонтальна проекція лінії перетину, збігається з '1; (B'1S'1A'1)'1; фронтальна проекція лінії перетину конус з площиною 'П1 — (B'2S'2A'2).
На рис. 1.75 показано фронтально-проектувальну площину , яка перетинає вісь фігури конуса під кутом > . У такому випадку лінією перетину є еліпс, який має велику і малу осі. Дійсна довжина великої осі еліпса збігається з фронтальним слідом площини 2 (12,22), горизонтальна проекція (1121) визначається за допомогою ліній проектувального зв’язку. Дійсна довжина малої осі еліпса визначається за допомогою площини-посередника (2), проведеної паралельно до площини П1, через середину великої осі (1222). Площина перетинає фігуру конуса по колу радіуса R(R2,R1), площину по прямій лінії m перпендикулярній до П2.
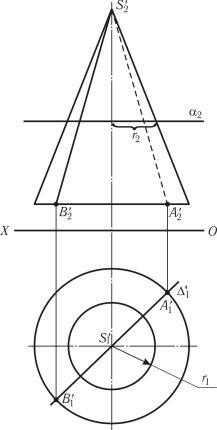
Рис. 1.74
Перетин горизонтальної проекції кола радіуса R1
з горизонтальною проекцією m1 визначає дійсну величину малої осі еліпса [3141]. Для побудови горизонтальної проекції еліпса існують декілька методів. Вони розглядались у середній школі, у вищій школі горизонтальна проекція еліпса виконується за допомогою площин-посередників. Для визначення проміжних точок застосовується площина – посередник '||П1, вона перетинає фігуру конуса по колу радіуса (r2, r1), площину по прямій лінії n (n2 n1). Перетин горизонтальної проекції кола радіуса r1 з n1 горизонтальної проекції визначає проміжні точки 51 61.Поєднання отриманих горизонтальних проекцій визначає горизонтальну проекцію еліпса.
.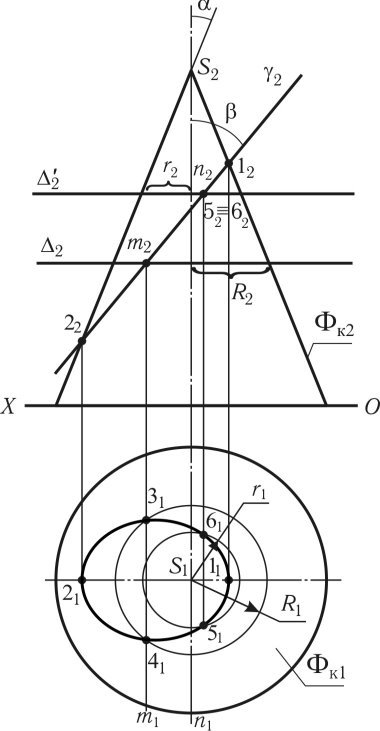
Рис. 1.75
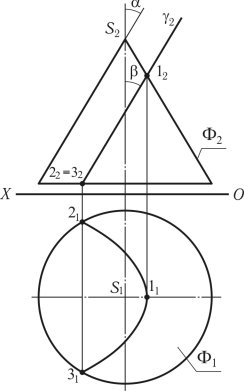
Рис. 1.76
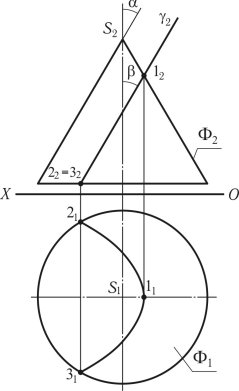
Рис. 1.77
Парабола утворюється у випадку, коли кут дорівнює куту ( = ), тоді лінія перетину є параболою. Побудову лінії перетину конуса фронтально-проектувальною площиною , коли в перетині утворюється парабола, показано на рис. 1.76.
На рис. 1.77 показано побудову лінії перетину конуса фронтально-проектувальною (![]() ) площиною. Гіпербола виконується, коли кут нахилу твірної до осі конуса більше кута нахилу сліду площини до осі, тобто >. Побудови видно з креслення. Фронтальні проекції точок і кутів нахилу визначаються при перетині площин з твірними. Горизонтальні проекції точок визначаються за допомогою ліній проектувального зв’язку.
) площиною. Гіпербола виконується, коли кут нахилу твірної до осі конуса більше кута нахилу сліду площини до осі, тобто >. Побудови видно з креслення. Фронтальні проекції точок і кутів нахилу визначаються при перетині площин з твірними. Горизонтальні проекції точок визначаються за допомогою ліній проектувального зв’язку.
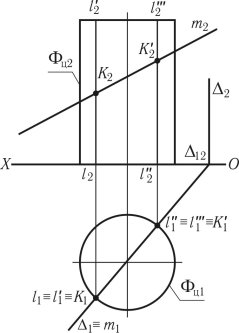
Рис. 1.78
1.8.3. Побудова точок перетину циліндра прямою лінією
На рис. 1.78 показано побудову проекцій точок перетину прямої лінії m (m1, m2) з фігурою циліндра Фц (Фц2Фц1). Для побудови точок перетину прямої лінії m з циліндром потрібно пряму лінію m залучити в горизонтально-проектувальну площину ∆. Площина перетинає циліндр (l'2l2)(l''2l'''2)(l1l'1)(l''1l'''1). Перетин m2 з (l'2l2) і m2 з (l''2l'''2) визначає фронтальні проекції точок входу і виходу прямої лінії з циліндра K2K'2. Горизонтальні проекції K1 і K'1 визначаються за допомогою ліній проектувального зв’язку. Пряма лінія m перетинає циліндр Фц в точках KK'.
1.8.4.Побудова лінії перетину двох поверхонь обертання
При побудові лінії перетину двох поверхонь обертання застосовуються два методи: метод січних куль і метод січних площин.
Побудову лінії перетину двох циліндрів методом січних куль показано на рис 1.79. Осі циліндрів І і ІІ перетинаються у точці О.
Циліндри різного діаметра, циліндр І має діаметр 1, циліндр II має діаметр 2. Діаметр 1 більше діаметра 2. Для визначення лінії перетину спочатку визначаються характерні точки 12; 22; 1'2; 2'2, які видно з побудови; вони знаходяться на перетині твірних циліндрів. Для визначення найнижчої точки лінії перетину 3 (32 і 3'2) застосовується куля, діаметр якої дорівнює діаметру більшого циліндру. Куля торкається циліндра І по колу (М2М'2), яке проектується на фронтальну площину проекцій в пряму лінію. Куля перетинає циліндр ІІ по двом колам, які проектуються в лінії (F2F'2) і (F''2F'''2). Перетин (М'2М2) з (F2F'2) визначає 32 — найнижчу проекцію точки лінії перетину, аналогічно визначається і 3'2.
Для визначення проміжних точок застосовується куля більшого діаметра, яка перетинає циліндр І по колу проекції (N2N'''2 і N'2N''2), циліндр ІІ по колу проекції (Т2Т'2 і Т'''2Т''2). Перетин відповідних проекцій кола визначає проміжні проекції точок 42, 4'2, 4''2, 4'''2. Поєднання отриманих проекцій точок визначає лінії перетину (12, 4'2, 32, 42, 22) (1'2, 4''2, 3'2, 4'''2, 2'2).
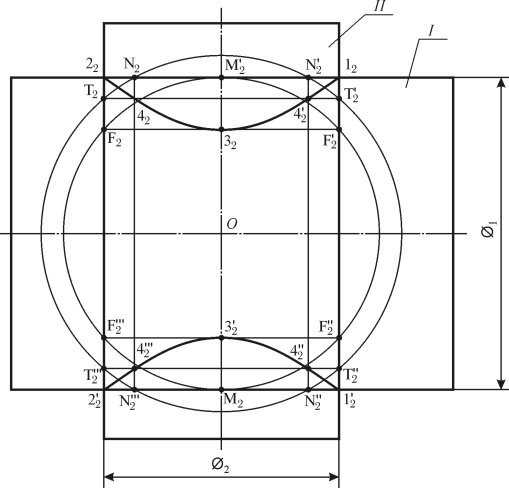
Рис. 1.79
На рис. 1.80 показано побудову лінії перетину поверхонь обертання кулі Фку і конуса Фк для випадку, коли центр кулі О' ’ вершина конуса S належать до площини, паралельної фронтальній площині проекцій. При побудові лінії перетину спочатку визначаються характерні точки, до яких належать найвища та найнижча точки (1, 2) лінії перетину, а також точки, які встановлюють межу видимості (3, 4). Проекції найвищої та найнижчої точок лінії перетину (12,22) (11,21) визначаються із побудови.
Точки, які вказують межу видимості (3,4), визначаються за допомогою горизонтальної площини-посередника 2 проходить через центр кулі О'2’ Площина перетинає кулю по колу, фронтальна проекція якого збігається зі слідом площини 2, горизонтальна проекція проектується в дійсну величину кола, яке має радіус R (R1 і R2). Одночасно площина перетинає фігуру конуса також по колу радіуса r (r2; r1), фронтальна проекція якого збігається зі слідом площини 2, яка проектується на горизонтальну площину в дійсну величину радіуса r1. Точки перетину проекцій фігури кола радіуса R1 і кола радіуса r1 визначають 31 41 — горизонтальні проекції точок, які показують межу видимості. Фронтальні проекції 32 42 визначаються за допомогою ліній зв’язку. Проміжні точки визначаються за допомогою площин-посередників. Так, наприклад, для визначення проміжних точок застосовується площина паралельна площині П1.
Площина (2) перетинає кулю по колу радіуса R' (R'1; R'2), фігуру конусу по колу радіуса r' (r'2; r'1). Перетин горизонтальних проекцій ліній перетину кулі і кола Фк(R'1) Фк(r'1) визначає горизонтальні проекції проміжних точок (5161). Фронтальні проекції точок (52 62) визначаються за допомогою ліній проектувального зв’язку. Фронтальна проекція лінії перетину (123242526222) і горизонтальна проекція лінії перетину фігури конуса з фігурою кулі (114161215131). Видимість визначається при застосуванні метода конкуруючих точок.
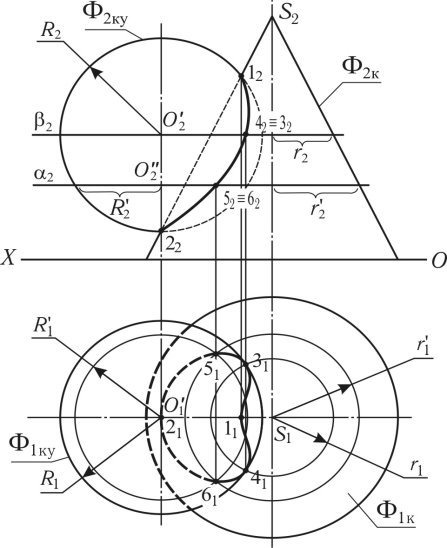
Рис. 1.80
Запитання для самоперевірки знань
1. Які методи застосовуються при побудові лінії перетину двох поверхонь обертання?
2. У чому полягає суть метода січних площин?
3. У чому полягає суть метода сфер?
Завдання для самоперевірки
Задача №1.
Побудувати лінію перетину конуса з горизонтально-проектувальною площиною.
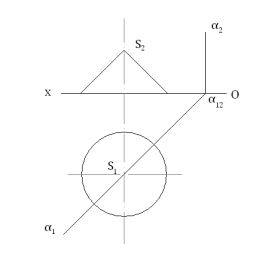
Задача №2.
Побудувати лінію перетину полу сфери з горизонтальною площиною рівня.
РОЗДІЛ 2. ЗАГАЛЬНІ ПРАВИЛА ВИКОНАННЯ КРЕСЛЕНЬ
- ВИДИ КОНСТРУКТОРСЬКИХ ДОКУМЕНТІВ
Згідно зі стандартом до конструкторських документів відносять графічні та текстові документи, які визначають склад і будову виробу. До графічних документів належать креслення деталі, складальне креслення, креслення загального вигляду, теоретичне, габаритне, монтажне, електромонтажне креслення та схеми.
До текстових документів належать специфікація, пояснювальна записка, технічні умови, відомості тощо.
При вивченні графічних дисциплін курсанти виконують розрахунково-графічні завдання за тематикою: геометричне, проекційне креслення, ескізування, креслення деталі, складальне креслення, схеми. Коло текстових документів, які вивчають на першому курсі, обмежується виконанням титульного аркуша та специфікації.
- ВИМОГИ СТАНДАРТІВ ДО ОФОРМЛЕННЯ КРЕСЛЕНЬ
2.2.1. Формати (ГОСТ 2.301 – 68).
2.2.2. Масштаби (ГОСТ 2.302 – 68).
2.2.3. Лінії креслення (ГОСТ 2.303 – 68).
2.2.4. Шрифти креслярські (ГОСТ 2.304 – 81).
2.2.5. Графічне позначення матеріалів на кресленнях (ГОСТ 2.306 – 68).
2.2.6. Нанесення розмірів (ГОСТ 2.307 – 68).
Правила оформлення конкретного конструкторського документа визначаються його специфікою і положенням відповідних стандартів. Розглянемо спочатку загальні правила оформлення креслень, що діють відповідно документації всіх галузей промисловості.
2.2.1. Формати (ГОСТ 2.301-68)
![]()
![]() Креслення й інші конструкторські документи виконують на форматах, визначених ГОСТом 2.301-68. Формати аркушів креслень визначають розміри зовнішньої рамки, яку викреслюють суцільною тонкою
Креслення й інші конструкторські документи виконують на форматах, визначених ГОСТом 2.301-68. Формати аркушів креслень визначають розміри зовнішньої рамки, яку викреслюють суцільною тонкою
лінією (рис. 2.1).
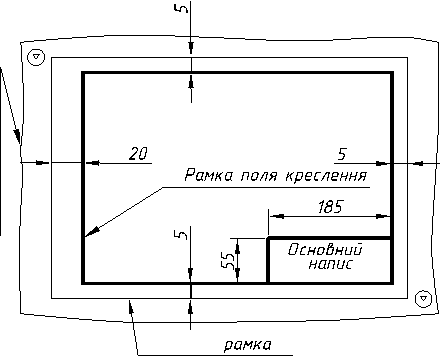
Рис. 2.1
Основні формати та їх позначення подані в табл. 2.1. - Розміри основних форматів
Таблиця 2.1
|
Позначення формату |
А0 |
А1 |
А2 |
А3 |
А4 |
|
Розміри сторін формату, мм |
841х1189 |
594х841 |
420х594 |
297х420 |
210х297 |
За необхідності допускається використання формату А5 з розмірами сторін 148х210 мм.
Площа формату А0 дорівнює 1м2. Кожен наступний формат меншого розміру одержують діленням навпіл попереднього формату паралельно його короткій стороні.
На рис. 2.1 вказано габарити основного напису (55х185), який завжди розміщують у правому нижньому куті формату, впритул до рамки, форму і зміст якого (рис. 2.2) регламентує ГОСТ 2.104 - 68. Слід пам’ятати, що на форматі А4 рамку основного напису слід викреслювати тільки вздовж короткої сторони формату. На інших форматах її можна розміщувати вздовж будь-якої сторони. Рамку поля креслення слід викреслювати суцільною товстою лінією товщиною не менше 0,7 мм.
Основний напис робіт із геометричного креслення слід виконувати за зразком, який наведено на рис. 2.2.
У графах основного напису (рис. 2.2) потрібно вказати:
у графі 1 –назву виробу, починаючи з іменника, і назву документа, якщо йому присвоєно шифр. Наприклад, для робочого креслення деталі – „Колесо зубчасте”; для схеми електричної принципової – Схема електрична принципова”;
у графі 2 – позначення документа відповідно до ГОСТ 2.202-80;
у графі 3 – позначення матеріалу деталі (графу заповнюють лише на кресленнях деталей);
у графі 4 – літеру, присвоєну цьому документові відповідно до ГОСТу 2.103-68;
у графі 5 – масу виробу відповідно до ГОСТу 2.109-73; на навчальних кресленнях не заповнюють;
у графі 6 – масштаб (проставляють згідно з ГОСТом 2.302-68);
у графі 7 – порядковий номер аркуша (на документах, що складаються з одного аркуша, графу не заповнюють);
у графі 8 – загальну кількість аркушів документа (графу заповнюють лише на першому аркуші).
Приклад заповнення основного напису на навчальому кресленні
(рис. 2.2):

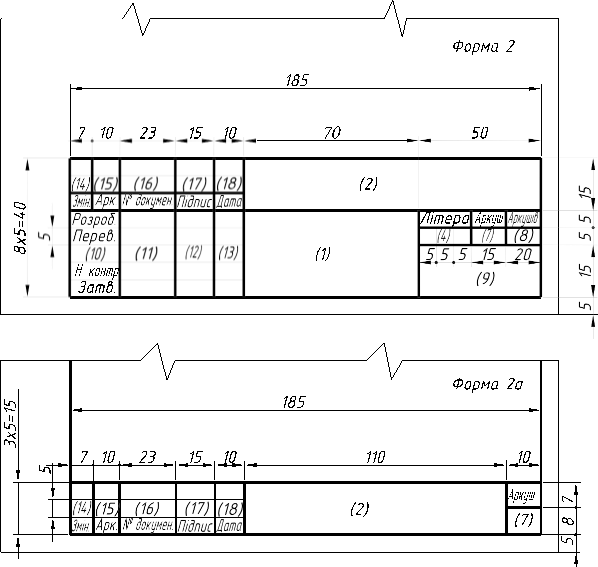
Рис. 2.2
- Масштаби (ГОСТ 2.302 – 68)
Масштабом називають відношення лінійних розмірів зображення на кресленні до його дійсних розмірів.
Переважно креслення виконують так, щоб розміри зображення й самого предмета були однакові, тобто в масштабі 1:1. Однак залежно від величини й складності предмета, а також вигляду креслення часто доводиться розміри зображення збільшувати або зменшувати у порівнянні з дійсними. У цих випадках будують зображення в масштабі.
Залежно від складності й величини зображуваних виробів масштаби, згідно з ГОСТом 2.302 – 68 вибирають із такого ряду:
Масштаби зменшення – 1:2; 1:2,5; 1:4: 1:5; 1:10; 1:15; 1:20; 1:25; 1:40;
1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000.
Дійсна величина – 1:1.
Масштаби збільшення – 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.
При проектуванні генеральних планів великих об’єктів допускається використання масштабів 1:2000; 1:5000; 1:10000; 1:20000; 1:25000; 1:50000.
За необхідності допускається використання масштабів збільшення
(100n):1, де n – ціле число.
При виборі масштабу слід керуватися, насамперед, зручністю користування кресленням. Масштаб, який вказують у графі, що має заголовок “Масштаби” (в основному написі, в таблицях), позначають: 1:1; 1:2; 2:1 і т. д. На полі креслення масштаб указують у дужках поряд із умовним позначенням зображення. Наприклад: А-А (2:1); Б1 (5:1); В (1:4).
- Лінії креслення (ГОСТ 2.303 – 68)
ГОСТ 2.303-68 встановлює 9 типів ліній залежно від їх товщини, зображення й основного призначення(табл. 2.2).
Товщина ліній на кресленні має бути кратною вибраній товщині суцільної основної лінії, товщина якої може змінюватися в межах від 0,5 до 1,4 мм. Товщина ліній повинна бути однаковою для усіх зображень на даному кресленні, які викреслюють в одному й тому ж масштабі.
Довжину штрихів у штрихових і штрих-пунктирних лініях вибирають залежно від величини зображення. Штрихи в лінії й проміжки між ними повинні бути однакової довжини.
Штрих-пунктирні лінії повинні починатися, перетинатися і закінчуватися штрихами. Штрих-пунктирні лінії, які використовують в якості центрових,
![]()
![]()
![]()
![]()
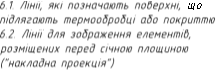
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
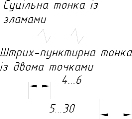
![]()
![]()
![]()
![]() Таблиця 2.2
Таблиця 2.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
замінюють суцільними тонкими лініями, якщо діаметр кола або розміри інших геометричних фігур у зображенні менші за 12 мм. Центр кола в усіх випадках визначають перетином штрихів.
У складних розрізах і перерізах допускається кінці розімкненої лінії з’єднувати шрих-пунктирною тонкою лінією. Довжину кінців розімкнених ліній вибирають у межах 8 – 20 мм залежно від розмірів зображення.
Основні лінії (лінії видимого контура) потрібно викреслювати товщиною 0,8…1,0 мм., лінії штрихові (лінії невидимого контуру) – 0,4…0,5 мм., а інші – 0,25…0,30 мм.
2.2.4. Шрифти креслярські (ГОСТ 2.304 – 81)
Згідно з ГОСТом 2.304 – 81 написи, які наносять на креслення та інші технічні документи всіх галузей промисловості та будівництва, виконують шрифтом з нахилом 75° до основи рядка або без нахилу, товщиною ліній шрифту 1:14 (тип А) або 1:10 (тип Б) від розміру (висоти) шрифту. Стандарт регламентує такі розміри шрифтів: (1,8); 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Розмір шрифтів визначають висотою великих букв у міліметрах. Розміри букв і цифр, товщину їх ліній, відстань між буквами, словами і рядками необхідно вибирати залежно від розміру або товщини ліній шрифту.
Для написів на кресленнях та інших конструкторських документах рекомендується використовувати шрифт типу Б як зручніший у написанні. При написанні шрифту необхідно спочатку побудувати олівцем сітку у вигляді тонких ліній, залежно від висоти букв і цифр. Перш ніж почати написання букв і цифр, потрібно вивчити їхню конструкцію та відносні розміри. Великі й малі букви умовно поділяють за спільністю однакових елементів і шириною на кілька груп (табл. 2.3). Сітку для всіх розмірів шрифту потрібно будувати олівцем під кутом 75° і вписувати в цій сітці кожну букву і цифру доти, допоки написані букви і цифри будуть виходити і без сітки, тобто коли курсант опанує вміння та навики вільного письма.
Послідовність написання і обводення прямолінійних елементів букв в основному здійснюють зверху вниз і зліва направо, а для криволінійних елементів букв – зверху вниз за годинниковою стрілкою або проти неї. Під час виконання креслень, як правило, використовують шрифти розмірів 3,5 і 5, а саме, при нанесенні розмірів, а також при виконанні текстових написів і заповненні граф специфікації. Розміри шрифтів 5 і 7 використовують в основному для назв деталей та позначення документа у відповідній графі основного напису креслення, а розмір 10 – для загальних заголовків.
Таблиця 2.3
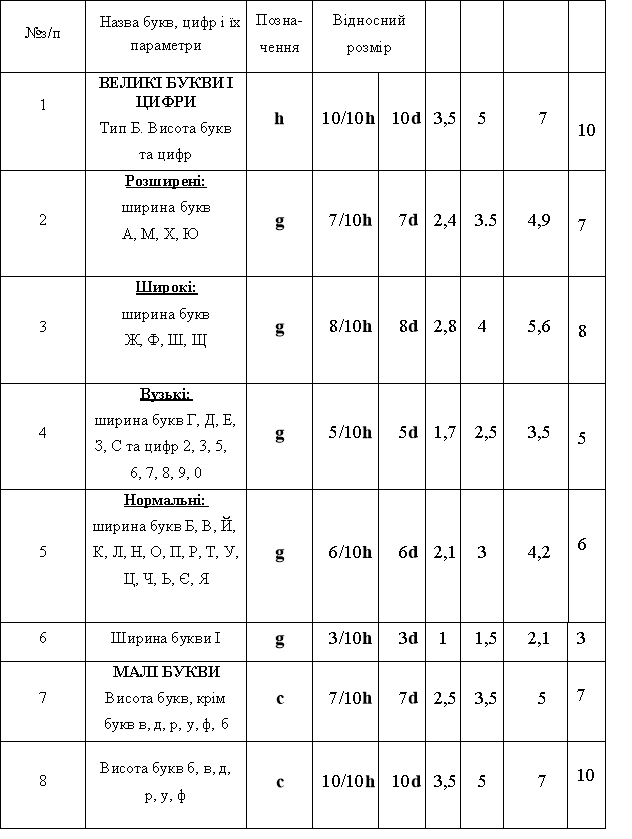
м
|
Продовження таблиці 2.3 |
||||||||
|
9 |
Нормальні: ширина букв а, б, в, г, д, е, и, й, к, л, н, о, п, р, у, х, ц, ч, ь, є, я |
g |
5/10h |
5d |
1,7 |
2,5 |
3,5 |
5 |
|
10 |
Розширені: ширина букв м, ю |
g |
6/10h |
6d |
2,1 |
3 |
4,2 |
6 |
|
11 |
Широкі: ширина букв ж, т, ф, ш, щ |
g |
7/10h |
7d |
2,4 |
3,5 |
4,9 |
7 |
|
12 |
Вузькі: ширина букв з, с |
g |
4/10h |
4d |
1,4 |
2 |
2,8 |
4 |
|
13 |
ВІДСТАНЬ МІЖ БУКВАМИ ТА ЦИФРАМИ |
а |
2/10h |
2d |
0,7 |
1 |
1,4 |
2 |
|
14 |
ВІДСТАНЬ МІЖ ОСНОВАМИ РЯДКІВ |
b |
17/10h |
17d |
6 |
8,5 |
12 |
17 |
|
15 |
МІНІМАЛЬНА ВІДСТАНЬ МІЖ СЛОВАМИ |
e |
6/10h |
6d |
2,1 |
3 |
4,2 |
6 |
|
16 |
ТОВЩИНА ЛІНІЙ ШРИФТУ |
d |
1/10h |
d |
0,35 |
0,5 |
0,7 |
1 |
2.2.5. Графічне позначення матеріалів на кресленнях
(ГОСТ 2.306 – 68)
Матеріал, із якого повинен бути виготовлений виріб, вказують відповідним чином у рамці основного напису креслення (графа 3, рис. 2.2). Для зручності користування кресленням у перерізах (у тому числі й ті, які входять до складу розрізів) наносять графічні позначення матеріалів, які характеризують матеріал тільки в загальних рисах. Деякі з них, які найчастіше зустрічаються на машинобудівних кресленнях, наведено в
таблиці 2.4. Паралельні лінії штриховок наносять під кутом 45до лінії рамки креслення (рис. 2.3) або до осі виносного чи накладного перерізів. Відстань між лініями – 1…10 мм залежно від площі перерізу (для навчальних креслень рекомендується 2…3мм). Вона повинна бути однаковою на всіх перерізах, які стосуються даної деталі і які виконані в одному і тому ж масштабі.
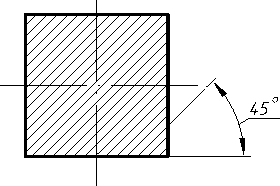

Рис. 2.3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.4
Таблиця 2.4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При співпаданні напряму ліній штриховки з контурними або осьовими лініями взамін кута нахилу штриховки 45° використовують кут 30° або 60° (рис.2.4).
Штриховку суміжних перерізів наносять для одного перерізу вправо, а для іншого – вліво, або ж змінюють крок штриховки. Використовують також зсув ліній штриховки.
Вузькі площини перерізів, ширина яких на кресленні не перевищує 2 мм, дозволяється зачорнювати.
2.2.6. Нанесення розмірів (ГОСТ 2.307 – 68)
Нанесення розмірів на кресленні – одна з найважливіших і відповідальних стадій його виконання. Виконують її згідно з такими основними вимогами ГОСТу – 2.307-68:
- Кожен розмір наносять на кресленні тільки один раз. Повторювати розміри на зображеннях або при нанесенні написів не дозволяється.
- Загальна кількість розмірів повинна бути мінімальною, але достатньою для того, щоб за цим кресленням можна було виготовити виріб і проконтролювати якість його виготовлення.
- Незалежно від масштабу на кресленні завжди проставляють дійсні розміри в міліметрах без позначення одиниці вимірювання.
- Розмірні лінії з обох кінців обмежують стрілками, що своїми кінцями впираються до відповідної лінії, яка є межею вимірювання (виносні, осьові, контурні) (рис. 2.5). Їх переважно наносять поза контуром зображення. Величина стрілок розмірних ліній залежить від товщини лінії видимого контуру (рис. 2.6). На навчальних кресленнях розмірні стрілки рекомендується наносити довжиною 5…7 мм.
- Мінімальна відстань між паралельними розмірними лініями – 7-10 мм, а між розмірною і лінією контуру – 10 мм (рис. 2.5).
- Виносні лінії є допоміжними. Їх проводять від межі вимірювання перпендикулярно прямолінійному відрізку елемента деталі, розмір якого наносять. Виносні лінії повинні виходити за кінці стрілок або засічок на 1…5 мм (рис.2.5).
- Лінії контуру, осьові, центрові й виносні не можна використовувати в якості розмірних ліній. Осьові і центрові лінії можуть бути використані як виносні. Для цього їх необхідно продовжити (рис. 2.5). Водночас не рекомендується допускати перетину розмірних і виносних ліній.
- Розмірні числа лінійних розмірів при різному нахилі розмірних ліній розміщують так, як зображено на рис. 2.7. Якщо необхідно вказати розмір у заштрихованій зоні, то розмірне число наносять на поличці – виносці (рис. 2.7).
- Стрілки на діаметрі кола або радіусі дуги повинні бути поверненими до лінії кола чи дуги. Розмірні лінії радіусів і діаметрів, нанесених на колах, не повинні займати горизонтального і вертикального положень чи співпадати з центровими лініями.
Рис. 2.5
![]()
![]()
Рис. 2.6
-

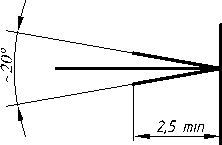
 Розмірні числа для радіусів необхідно доповнювати позначенням на взірець R10, R25, де висота букви дорівнює висоті цифри. Розмірні числа діаметрів доповнюють умовним знаком Ø, який проставляють перед розмірним числом на взірець Ø15 (рис. 2.5).
Розмірні числа для радіусів необхідно доповнювати позначенням на взірець R10, R25, де висота букви дорівнює висоті цифри. Розмірні числа діаметрів доповнюють умовним знаком Ø, який проставляють перед розмірним числом на взірець Ø15 (рис. 2.5).
![]()
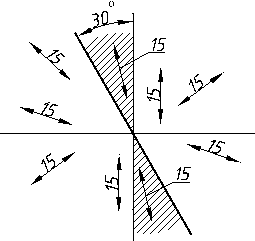
Рис. 2.7
- Якщо при нанесенні розмірного числа не вистачає місця між розмірними стрілками, його наносять, як це зображено на рис 2.9, розміщуючи по можливості число з правого боку.

Рис. 2.8
- Якщо при нанесенні розмірного числа не вистачає місця для стрілок, їх можна проставляти із зовнішнього боку або можна замінити засічками, які наносять під кутом 45° до розмірної лінії за ходом напису, або чітко нанесеними точками (рис. 2.10).
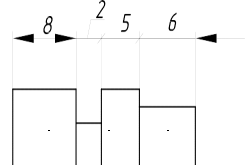
Рис. 2.9
-

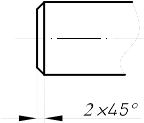 Конічні фаски, виконані на кінцях циліндричних деталей під кутом 45°, позначають як добуток величини катета на його кут: 2х45°. Якщо на кресленні даної деталі є кілька однакових конічних фасок, то їх позначають як 2 фаски 2х45°(рис. 2.10). При інших кутах виконання фаски її вказують так, як це зображено на рис. 2.10в, тобто окремо вказують розмір катета і розмір кута.
Конічні фаски, виконані на кінцях циліндричних деталей під кутом 45°, позначають як добуток величини катета на його кут: 2х45°. Якщо на кресленні даної деталі є кілька однакових конічних фасок, то їх позначають як 2 фаски 2х45°(рис. 2.10). При інших кутах виконання фаски її вказують так, як це зображено на рис. 2.10в, тобто окремо вказують розмір катета і розмір кута.
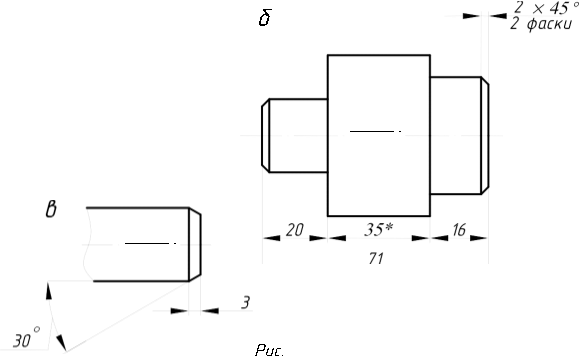
Рис. 2.10
-
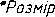 При нанесенні розмірів використовують також інші знаки та умовності, які дозволяють скоротити кількість зображень і розмірів.
При нанесенні розмірів використовують також інші знаки та умовності, які дозволяють скоротити кількість зображень і розмірів.
- Розміри проставляють за принципом “незамкненого ланцюга”, за винятком будівельних креслень. Замкнений ланцюг допускається, якщо один із розмірів вказується як довідковий. Цей розмір позначають зірочкою (*), а в технічних вимогах записують: “Розмір для довідок” (рис. 2.10.б).
- Над паралельними або концентричними розмірними лініями розмірні числа розміщують у шаховому порядку (рис. 2.11).
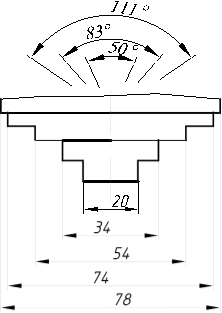
Рис. 2.11
- Коли не вистачає місця для стрілки через близьке розміщення контурної лінії, останню можна розривати (рис. 2.12).
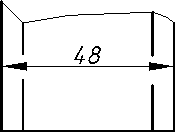
Рис. 2.12
- Розміри кута, хорди та дуги кола наносять так, як це зображено на рис.2.13. Кутові розміри наносять так, як це зображено на рис.2.14. При цьому для кутів малих розмірів розмірні числа розміщують на поличках ліній-виносок у будь- якій зоні.
![]()
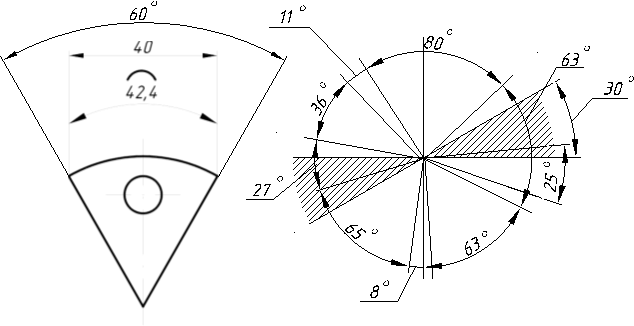
Рис. 2.13 Рис. 2.14
-
 Якщо потрібно нанести координати вершини кута заокруглення або центр дуги заокруглення, то виносні лінії проводять від точки перетину сторін кута заокруглення або від центра дуги заокруглення (рис. 2.15).
Якщо потрібно нанести координати вершини кута заокруглення або центр дуги заокруглення, то виносні лінії проводять від точки перетину сторін кута заокруглення або від центра дуги заокруглення (рис. 2.15).
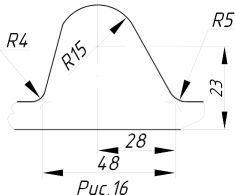
Рис. 2.15
- Якщо вигляд або розріз симетричного предмета або окремих симетрично розміщених елементів зображують тільки до осі симетрії або з обривом, то розмірні лінії, які відносяться до цих елементів, проводять з обривом і обрив розмірної лінії виконують за віссю або за лінією обриву предмета (рис. 2.16а).
Розмірні лінії можна проводити з обривом і при зображенні розміру діаметрів кола незалежно від того, зображено коло цілком чи частково, при цьому обрив розмірної лінії виконують за центром кола (рис. 2.16б).

![]()
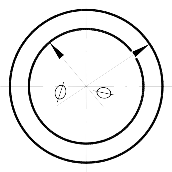
![]()
Рис. 2.16
- При зображенні виробу з розривом розмірну лінію не розривають (рис.2.17).
- Розмірні числа неможна розділяти або перетинати будь-якими лініями креслення. Не допускається розривати лінію контуру при нанесенні розмірного числа та наносити розмірні числа в місцях перетину розмірних, осьових або центрових ліній. Осьові, центрові лінії та лінії штриховки допускається розривати (рис. 2.18).
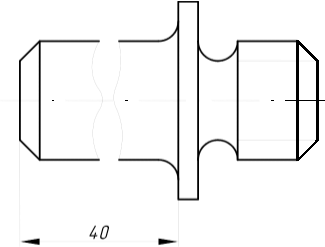
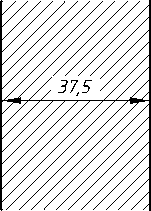
Рис. 2.17 Рис. 2.18
- Якщо при нанесенні розміру радіуса дуги кола необхідно нанести розмір, який визначає положення її центра, то його зображують у вигляді перетину центрових або виносних ліній, причому при великій величині радіуса центр дозволяється наближувати до дуги. В цьому випадку розмірну лінію радіуса зображують з зламом під кутом 90(рис.2.19).
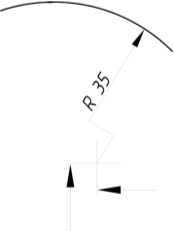
Рис. 2.19
- При співпаданні центрів кількох радіусів їх розмірні лінії можна не доводити до центра, крім крайніх (рис.2.20).
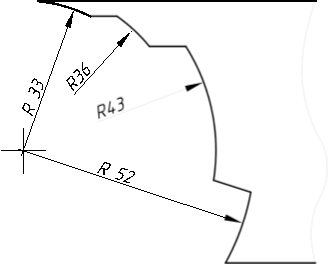
Рис. 2.20
-
 Розміри діаметрів виробу складної конфігурації можна наносити так, як зображено на рис. 2.21. У випадках, коли сферу важко відрізнити від інших поверхонь, наносять слово “Сфера” або знак згідно з рис.2.22. Діаметр знака сфери дорівнює розміру розмірних чисел на кресленні.
Розміри діаметрів виробу складної конфігурації можна наносити так, як зображено на рис. 2.21. У випадках, коли сферу важко відрізнити від інших поверхонь, наносять слово “Сфера” або знак згідно з рис.2.22. Діаметр знака сфери дорівнює розміру розмірних чисел на кресленні.
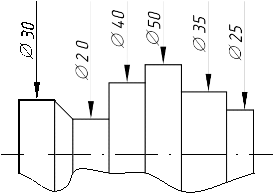
Рис. 2.21
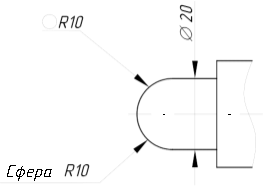
Рис. 2.22
- Розмір квадрата наносять так, як зображено на рис. 2.23. Висота знака “квадрат” дорівнює висоті цифр розмірних чисел на кресленні.
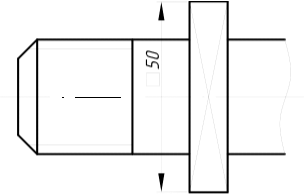
Рис. 2.23 Рис. 2.24
- Якщо креслення містить одне зображення деталі, то розмір її товщини або довжини наносять так, як це зображено на рис. 2.24 та рис. 2.25.

Рис. 2.25
- Розміри виробу завжди наносять номінальні, незалежно від масштабу зображення. Якщо елемент зображено з відхиленням від масштабу, то розмірне число підкреслюють (рис. 2.26). Це правило не поширюється на випадки, коли деякі елементи зображення важко викреслити або бажано збільшити їх зорове сприйняття, а також при зображенні в М1:1 тонких пластин, прокладок, шайб.

Рис. 2.26
- Розмірні лінії бажано наносити поза контуром зображення, в міру можливості розміщуючи внутрішні та зовнішні розміри деталі з різних боків зображення (рис. 2.27). Але розміри можна нанести і в середині контуру зображення, якщо креслення від цього не втрачає зрозумілості.

Рис. 2.27
- Нанесення розмірів на невидимому контурі дозволяють у тих випадках, коли це дозволяє відмовитися від викреслення додаткового зображення (рис. 2.28).
Рис. 2.28
- Для того, щоб вірно нанести розміри, необхідно спочатку вибрати бази для їх відліку.
Розмірні бази – це опорні оброблені поверхні деталі або геометричні осі основних її елементів, відносно яких визначають положення інших поверхонь, ліній або точок. При цьому враховують призначення деталі в машині або вузлі. Згідно з ГОСТом 21495-76 бази поділяють на конструкторські (основні та допоміжні), технологічні та вимірювальні. Конструкторські бази є координатними площинами, які дозволяють точно визначити положення у виробі будь-якої складальної одиниці або деталі.
Технологічна база визначає положення заготовки або виробу при їх виготовленні або ремонті.
Вимірювальна база визначає відносне положення заготовки або виробу та засобів вимірювання.
-
Базами відліку можуть бути:
- Площини, з яких починається обробка, наприклад, торцеві, привалкові та інші. На рис. 2.29 зображено деталь, у якої основні (конструкторські) бази – це привалкова площина А та геометрична вісь деталі. Від них відраховують розміри а, в, с, d діаметри 1, 2, і т. д.
- Прямі лінії, наприклад, осі симетрії, будь-які взаємно перпендикулярні кромки деталі та інше.
При цьому розміри, які відносяться до одного і того ж елемента (канавки, виступи і т. д.), рекомендується концентрувати в одному місці, розміщуючи їх на тому зображенні, на якому цей елемент зображений найчіткіше (рис. 2.30).
Рис. 2.29
- Точка. На рис. 2.31 зображено кулачок механізму автомата. Тут база – точка О (полюс системи полярних координат). Для відліку кутів базою служить пряма ОХ (полярна вісь).
- При нанесенні розмірів необхідно також ураховувати й технологію виготовлення деталі.
У конструкціях машин часто можна зустріти вали та інші круглі деталі, які обробляють на токарних або револьверних верстатах (рис. 2.32).
Рис. 2.32б ілюструє приклад неправильного нанесення розмірів і невдало вибраний варіант обробки такого валика, тому що обробити деталь з однієї установки в даному випадку неможливо (крім того, при обточуванні циліндра малого діаметра виникне велике осьове биття).
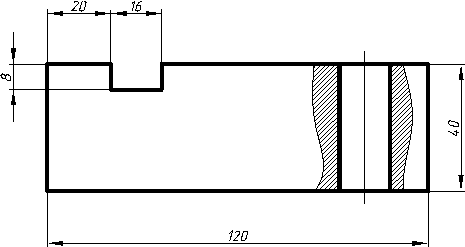
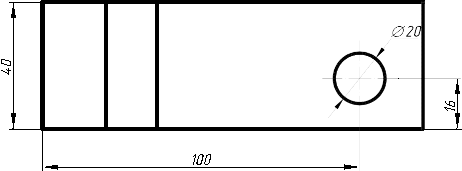
Рис. 2.30
![]()
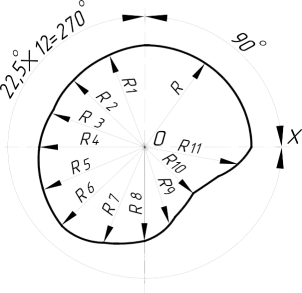
Рис. 2.31
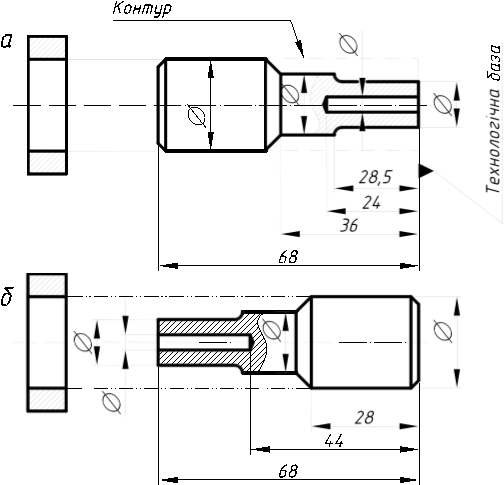
Рис. 2.32
- При нанесенні розмірів на креслення слід використовувати ряди чисел, яким треба надавати перевагу, враховуючи вимоги відповідних стандартів. Нормальні конусності й кути конусів (ГОСТ 8593-81) подано в табл. 2.5, нормальні лінійні розміри – в табл. 2.6, нормальні радіуси скруглень і фаски – в табл. 2.7 (ГОСТ 10948-64). При користуванні таблицями слід надавати перевагу першому ряду перед другим, другому – перед третім і т. д.
Таблиця 2.5
|
Конусність с |
Кут конуса α |
Конусність с |
Кут конуса α° |
|
1:500 |
6′52,5″ |
1:6 |
9°31′38,2″ |
|
1:200 |
17′11,3″ |
1:5 |
11°25′16,3″ |
|
1:100 |
34′22,6″ |
1:4 |
14°15′0,1″ |
|
1:50 |
1°8′45,2″ |
1:3 |
18°55′28,7″ |
|
1:30 |
1°54′34,9″ |
1:1,866025 |
30° |
|
1:20 |
2°51′51,1″ |
1:1,207107 |
45° |
|
1:15 |
3°49′5,9″ |
1:0,866025 |
60° |
|
1:12 |
4°46′18,8″ |
1:0,651613 |
75° |
|
1:10 |
5°43′29,3″ |
1:0,500000 |
90° |
|
1:8 |
7°9′9,6″ |
1:0,288675 |
120° |
|
1:7 |
8°10′16,4″ |
|
|
Таблиця 2.6
|
1-й ряд |
10; 11; 12; 14; 16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50; 56; 63; 71; 80; 90 |
|
2-й ряд |
10; 10.5; 11; 12; 13; 14; 16; 17; 18; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56; 60; 63; 67; 71; 75; 80; 85; 90; 95 |
Примітка: інші нормальні розміри отримують діленням або множенням чисел в інтервалі від 10 до 95 на 10n.
Таблиця 2.7
|
1-й ряд |
… 1.0; 1.6; 2.5; 4.0; 6.0; 10; 16; 25; 40… |
|
2-й ряд |
…1.0; 1.2; 1.6; 2.0; 2.5; 3.0; 4,0; 5,0; 6,0; 8,0; 10; 12; 16; 20; 25; 32; 40; 50… |
Запитання для самоперевірки.
- . Які розміри має зовнішня рамка формату А3?
- . Що називають масштабом зображення? Як позначають масштаб в основному написі креслення?
- . Які елементи креслення виконують суцільною тонкою лінією?
- . Яку висоту мають малі літери шрифту розміру 5?
- . Якою має бути мінімальна відстань між розмірною лінією та лінією контура при нанесенні розмірів?
- . Які знаки ставлять перед розмірним числом при нанесенні розміру радіуса або діаметра?
Завдання для самостійної роботи.
- . Накреслити зображення деталі у масштабі 4:1 (рис. 2.33).
- . Написати на полицях ліній-виносок назви ліній та їхнє функціональне призначення (рис. 2.34).
- . Нанести на зображення необхідні розміри деталі (рис. 2.35).
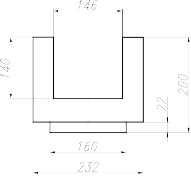
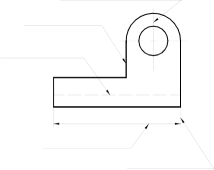
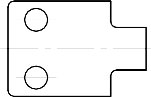
Рис. 2.33 Рис. 2.34 Рис. 2.35
- ГЕОМЕТРИЧНІ ПОБУДОВИ
2.3.1. Поділ відрізка на дві рівні частини.
2.3.2. Побудова перпендикуляра до прямої з точки, яка лежить поза прямою.
2.3.3. Поділ кола на три рівних частини.
2.3.4. Поділ кола на п’ять рівних частин.
2.4.5. Поділ кола на шість рівних частин.
2.3.6. Нахил.
2.3.7. Конусність.
2.3.8. Спряження.
Геометричною побудовою називаєть графічний метод розв’язування геометричних задач на площині за допомогою креслярських інструментів.
При вивченні розділу “Геометричне креслення” передбачається, що курсант володіє навиками користування креслярським інструментом та елементарними побудовами за допомогою кутника, лінійки, циркуля.
![]() 2.3.1. Поділ відрізка на дві рівні частини.
2.3.1. Поділ відрізка на дві рівні частини.
Цю побудову можна виконати за допомогою трикутника і циркуля. За допомогою трикутника через кінці А і В відрізка (рис. 2.37) проводять прямі під рівними кутами до відрізка АВ до їх взаємного перетину в точці С. Потім із точки С опускають перпендикуляр на АВ, який і поділить відрізок на дві рівні частини.
![]()
![]()
![]()
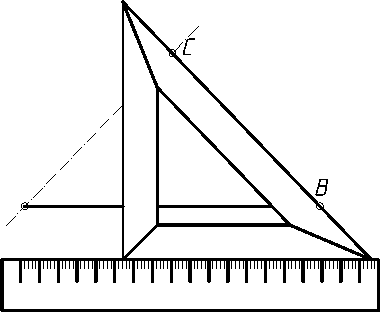
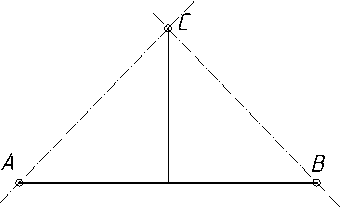

Рис. 2.37
Щоб поділити відрізок на дві рівні частини за допомогою циркуля
(рис. 2.38) з кінців А і В відрізка як із центрів радіусом R, більшим половини відрізка, проводять дуги до взаємного перетину в точках С і D. З’єднавши ці точки, ділять відрізок АВ точкою Е на дві рівні частини. Цей спосіб є також способом проведення перпендикуляра через середину відрізка.
![]()
![]()
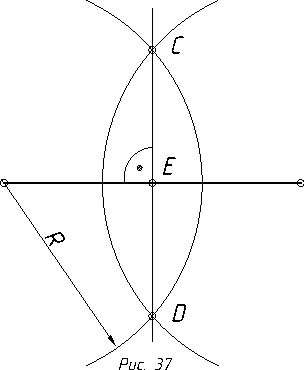
Рис. 2.38
2.3.2.Побудова перпендикуляра до прямої з точки, яка лежить поза прямою.
З точки С (рис. 2.39) як із центра проводять дугу кола довільного радіуса R, який перетинає пряму а в точках 1 і 2. Із цих точок як із центрів проводять дуги кіл також довільного радіуса R1 до взаємного перетину в точці D. Пряма, проведена через точки С і D, перпендикулярна до заданої прямої.
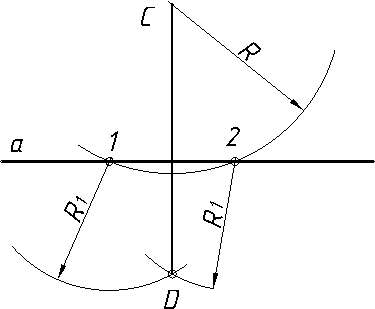
Рис. 2.39
2.3.3.Поділ кола на три рівних частини.
З точки С кола (рис. 2.40) радіусом R засікають на ньому точки 1 і 2. Дуга 1-2 і є третиною довжини кола. Радіусом, який дорівнює хорді 1-2, із точки 1 на колі засікають точку 3. Точки 1, 2 і 3 ділять коло на три рівних частини. Трикутник 1-2-3 рівносторонній, вписаний у коло.
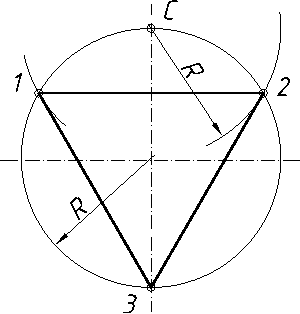
Рис. 2.40
2.3.4.Поділ кола на п’ять рівних частин.
Із середини радіуса-точки С (рис. 2.41), як із центра дугою радіуса CD засікають на діаметрі точку М. Відрізок DM визначає довжину сторони вписаного правильного п’ятикутника. Побудова вершин п’ятикутника зрозуміла із креслення.
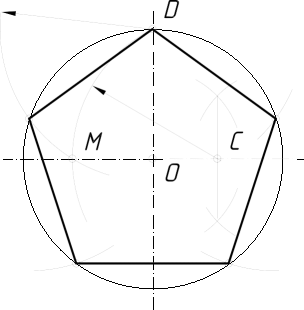
Рис. 2.41
2.4.5.Поділ кола на шість рівних частин.
Сторона правильного шестикутника, який вписаний в коло, дорівнює радіусу кола. Усі побудови зрозумілі з рис. 2.42.

Рис. 2.42
2.3.6. Нахил.
При викресленні багатьох технічних деталей доводиться будувати геометричні нахили, наприклад, при виготовленні профілю прокату, таких як швелер та двотавр, номер яких вказує на їх висоту в сантиметрах.
Нахилом прямої ВС відносно горизонтальної прямої АВ називають відношення i=h/l=tgφ, де φ– кут нахилу.
 На рис. 2.43 зображено побудову внутрішніх граней поличок швелера, нахил яких складає 10%.
На рис. 2.43 зображено побудову внутрішніх граней поличок швелера, нахил яких складає 10%.
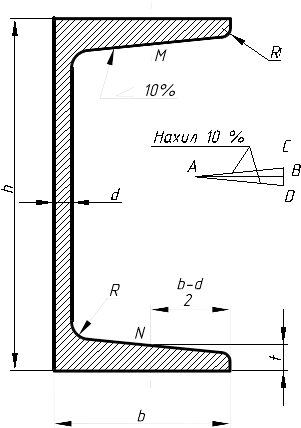
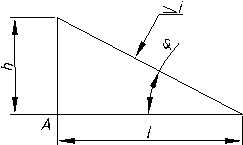
![]()
![]()
![]()
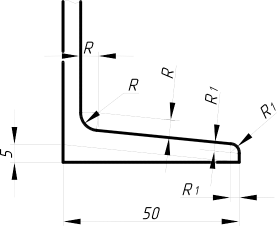
![]()
Рис. 2.43
Побудову нахилу поличок виконують у такій послідовності:
- Поряд з профілем на горизонтальній прямій АВ відкладають 10 довільних, однакової довжини відрізків, а на перпендикулярі в точці В відкладають з обидвох боків по одному такому ж відрізку. Гіпотенузи АС і АВ мають нахил 10%.
- Через точки М і N, які знаходяться на відстані (b-d)/2 від торця поличок і на висоті t від зовнішніх горизонтальних (нижньої і верхньої) граней поличок, проводять похилі лінії, відповідно паралельні до АС і AD. Після цього виконують заокруглення тупих кутів радіусами R і R1 (рис. 2.43). Аналогічно будують нахил поличок для двотаврових балок.
Знак нахилу ˃, вершина якого повинна бути направлена в бік нахилу, наносять перед розмірним числом, розміщуючи його безпосередньо біля зображення поверхні нахилу (рис. 2.43). Невеликий нахил на кресленні допускається зображувати збільшеним.
2.3.7. Конусність.
Конусністю називають відношення різниці діаметрів основ прямого кругового конуса до його висоти К=(D–d)/l. При одному і тому ж куті конусність у 2h рази більша за нахил (рис. 2.44).
![]()
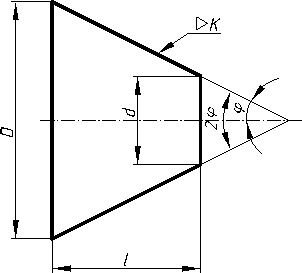
![]()
![]()
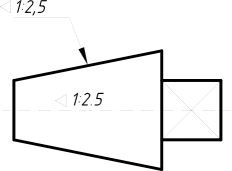
Рис. 2.44
Перед розмірним числом конусності наносять умовний знак, вершину якого направляють у бік вершини конуса (рис. 2.44).
2.3.8. Спряження.
Обриси багатьох технічних форм складаються з ліній, які плавно переходять одна в іншу. Плавний перехід однієї лінії в іншу називають спряженням. Із всієї багатоманітності спряжень різноманітних ліній можна виділити такі основні їх види: спряження прямої лінії з дугою кола, спряження двох по різному розміщених прямих ліній за допомогою дуги кола, спряження дуг двох кіл за допомогою прямої лінії і спряження дуг двох кіл за допомогою третьої.
Дуги кіл, за допомогою яких виконують спряження, називають дугами спряження. Для побудови дуги спряження необхідно на кресленні знайти її центр, радіус і точки спряження, в яких дуга спряження переходить у спряжені лінії. Задаючись одним із цих параметрів, інші можна визначити графічно.
При спряженні прямої лінії з дугою кола перша виконує роль дотичної до кола. В цьому випадку центр дуги кола О і точки спряження К лежить на перпендикулярі до спряженої прямої (рис. 2.45). При спряженні дуг двох кіл точка спряження К повинна лежати на лінії, яка з’єднує центри спряжених дуг (рис. 2.46).
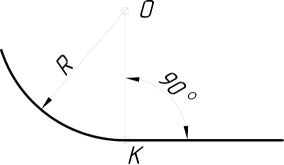
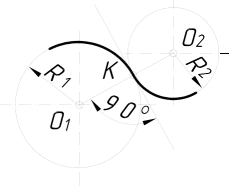
Рис. 2.45 Рис. 2.46
2.3.8.1.Спряження прямих ліній, які перетинаються за допомогою дуги.
Для побудови спряження двох взаємно перпендикулярних прямих а і в дугою кола заданого радіуса R (рис. 2.47) необхідно із точки перетину прямих як із центра провести дугу кола радіусом R до перетину з прямими в точках А і В (а). Із отриманих точок як із центрів тим же радіусом провести дуги кіл до взаємного перетину в точці О (б). Із точки О радіусом R провести дугу спряження (в). Точки А і В в даному випадку є точками спряження.
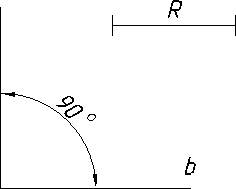
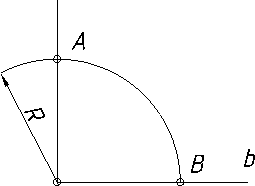
![]()
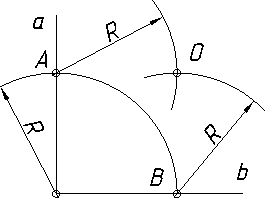
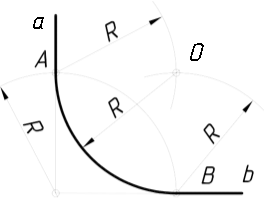
![]()
![]()
Рис. 2.47
Для побудови спряження двох прямих, які перетинаються, а і в, під гострим кутом дугою заданого радіуса R (рис. 2.48) необхідно визначити множину центрів кіл які віддалені від прямих на відстані R. Для цього на відстані R проводять прямі, які паралельні до заданих, до перетину в точці О (а). Дуга радіуса R, проведена із точки О як із центра, буде дугою спряження (б). Основи перпендикулярів, опущених із точки О на прямі а і в, будуть точками спряження.
Побудову спряження двох прямих, які перетинаються під тупим кутом дугою заданого радіуса R (рис. 2.49), виконують аналогічно з попереднім.
![]()
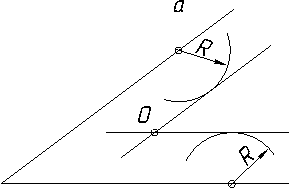
![]()
![]()

![]()
Рис. 2.48
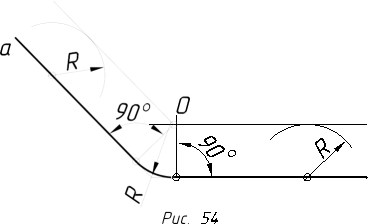
![]()
Рис. 2.49
2.3.8.2. Спряження паралельних прямих дугою кола.
Якщо на одній із прямих а і в задана точка спряження А (рис. 2.50), спряження виконують так. Із точки А опускають перпендикуляр на пряму в (а). Ділять відрізок АВ навпіл (б) і з точки О як із центра проводять дугу спряження радіусом ОА (в).
![]()
![]()
![]()
![]()
![]()
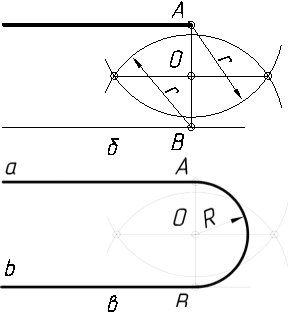
Рис. 2.50
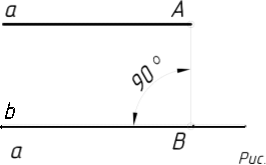 2.3.8.3. Спряження дуги кола радіуса R і прямої а дугою заданого радіуса R1.
2.3.8.3. Спряження дуги кола радіуса R і прямої а дугою заданого радіуса R1.
Для виконання цього спряження (рис. 2.51) спочатку визначають множину центрів дуг радіуса R1. Для цього на відстані R1 від прямої а проводять паралельну до неї пряму m, а із центра О радіусом (R+R1) дугу концентричного кола. Точка О1 буде центром дуги спряження. Точка спряження С, отримана на перпендикулярі, який опущений із точки О1 на пряму а, а точка В на прямій, яка з’єднує точки О і О1.
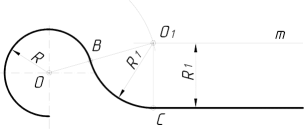
![]()
Рис. 2.51
2.3.8.4. Спряження дуг двох кіл за допомогою прямої лінії. Це спряження зводиться до побудови зовнішньої або внутрішньої дотичної до даних кіл (рис. 2.52).
Для проведення зовнішньої дотичної, яка спрягає два кола радіусами R і R1 (а), спочатку з’єднують центри кіл, потім відрізок ОО1 ділять точкою О2 навпіл, а із точки О проводять коло радіусом (R-R1), який дорівнює різниці радіусів заданих кіл (б). На цьому колі радіусом О2О засікають точки Е і D (в). Продовживши відрізки ОЕ і ОD до перетину з колом радіуса R, отримують точки спряження С і В (г). З’єднують точки Е і D із центром О1. Із точок С і В паралельно відрізкам О1Е і О1D проводять відрізки, які спрягають два кола. Точки спряження на колі радіуса R1 можна отримати, провівши з точки О1 перпендикуляри до відрізків О1Е і О1D.
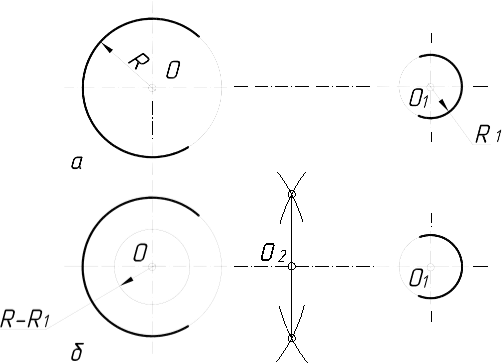
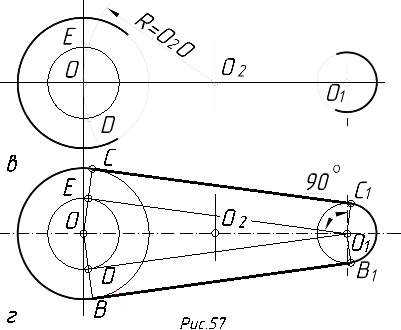
Рис. 2.52
Для побудови внутрішніх дотичних, які спрягають два кола радіусів R і R1 (рис. 2.53), із середини відрізка ОО1 точки О2 проводять дугу радіусом ОО2, а із центра О проводять дугу радіусом (R+R1), який дорівнює сумі радіусів заданих кіл (б). У перетині цих кіл позначають точки Е і D, які з’єднують з точкою О1. Дотичні, які спрягають два кола, будуть паралельними до відрізків ЕО1 і DO1 (в). Побудова точок спряження зрозуміла з креслення.

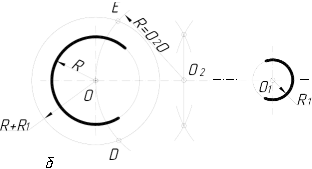
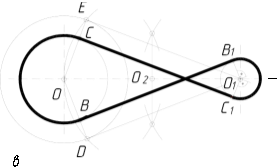
Рис. 2.53
2.3.8.5.Побудова спряження двох дуг кіл.
Спряження двох дуг кіл може бути зовнішнім і внутрішнім. На рис. 2.54а зображено зовнішнє спряження двох дуг кіл, а на рис 2.54б – внутрішнє. Точка спряження лежить на прямій, яка з’єднує центри кіл. Відстань між центрами в першому випадку повинна дорівнювати сумі радіусів кіл (R+R1), а в другому – різниці цих радіусів (R-R1). У точках спряження А кола мають спільну дотичну t.
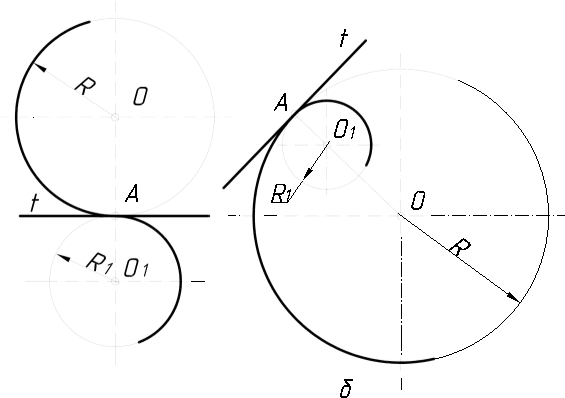
Рис. 2.54
-
 Побудова спряження двох дуг кіл дугою заданого радіуса.
Побудова спряження двох дуг кіл дугою заданого радіуса.
Такий вид спряження може бути зовнішнім, внутрішнім і змішаним. При зовнішньому спряженні дуги знаходяться з зовнішнього боку дуги спряження, тобто точки спряження є точками перегину.
На рис. 2.55 наведено приклад побудови зовнішнього спряження двох дуг кіл радіусів R і R1 за допомогою дуги радіуса R2. Із центра О радіусом (R+R2), а із центра О1 радіусом (R1+R2) проводять дуги до перетину в точці О2 (а). Точки спряження В і С лежать на лініях, які з’єднують точку О2 із центрами дуг О і О1. Із точки О2 як із центра проводять дугу спряження радіусом R2 (б).
Внутрішнє спряження дуг кіл за допомогою третьої характеризується тим, що спрягаємі дуги знаходяться в середині дуги спряження, тобто дуга спряження і спряжувальні дуги знаходяться по один бік дотичних, проведених через точки спряження. Точки спряження в цьому випадку є точками самодотику. На рис. 2.56 зображено внутрішнє спряження. Задані спряжувальні дуги радіусів R і R1 і радіус спряжувальної дуги R2. Із центра О проводять дугу радіусом (R2-R), а із центра О1 – дугу радіусом, який дорівнює ((R2-R1). У перетині цих дуг отримують точку О2 із центрами заданих кіл О і О1.
![]()
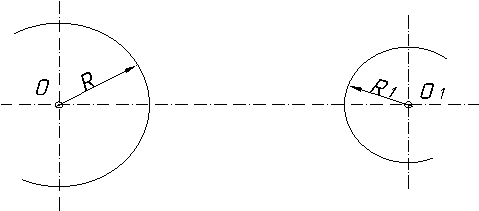
![]()
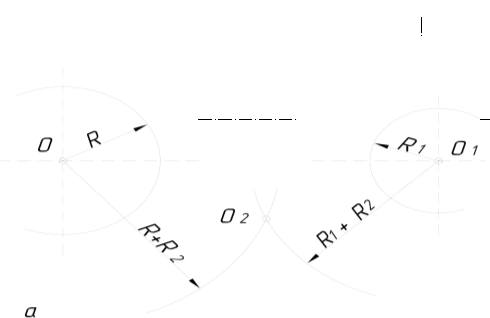
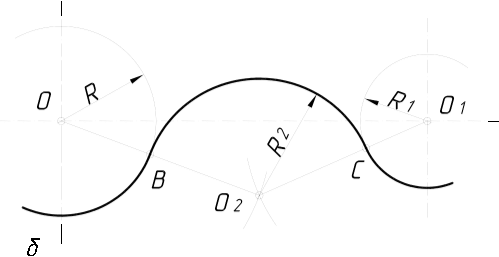
Рис. 2.55
![]()
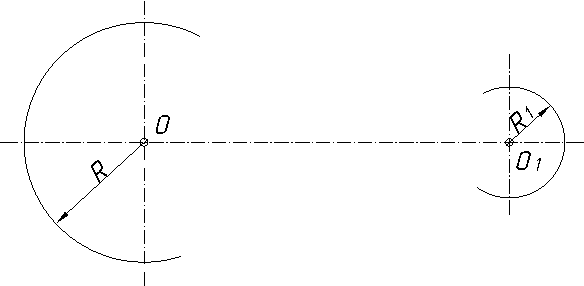

Рис. 2.56
Змішане спряження двох даних дуг кіл третьою дугою характеризується тим, що одна спряжувальна дуга знаходиться в середині дуги спряження, а інша поза нею, тобто одна точка спряження є точкою самодотику, а
інша – точкою перегину.
На рис. 2.57 наведено приклад змішаного спряження двох дуг кіл третьою дугою радіуса R2. Із центра О (а) проводять дугу радіусом (R2-R), а із центра О1
- радіусом (R2+R1). Перетин проведених дуг визначає центр дуги спряження. Дуга спряження з дугою радіуса R має внутрішнє спряження, а з дугою радіуса R1 – зовнішнє. Точка В – точка самодотику, а точка В1 – точка перегину.
На рис. 2.57б побудовано змішане спряження тих же дуг з тією різницею, що тепер дуга спряження з дугою радіуса R спрягається зовнішньо, а з дугою радіуса R1 – внутрішньо. Точка В стала точкою перегину, а точка В1 – точкою самодотику.
На рис. 2.58 наведено випадок змішаного спряження двох дуг кіл третьою дугою заданого радіуса R2, коли відстань а між центрами дуг менша суми їх радіусів (R+R1). Побудова зрозуміла з креслення.
![]()
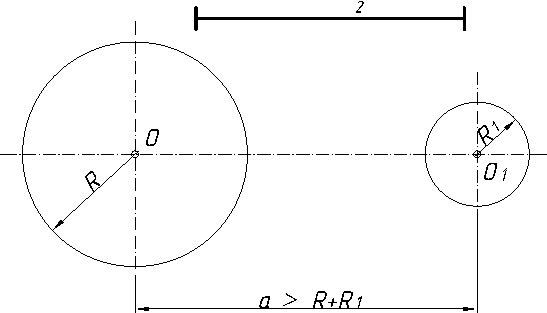

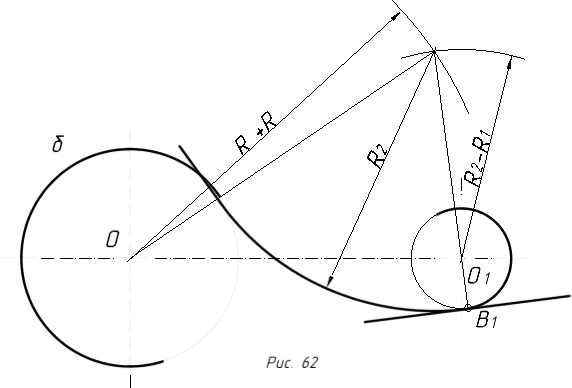
Рис. 2.57
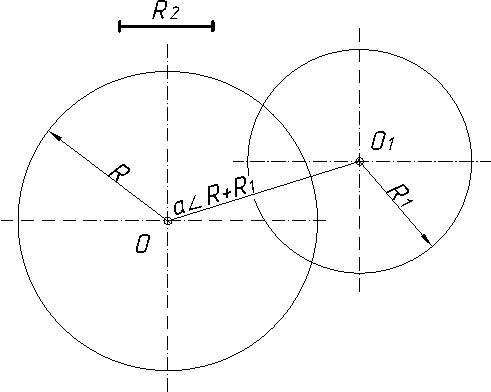

Рис. 2.58
Запитання для самоперевірки
1. Як побудувати перпендикуляр до прямої з точки, що лежить поза прямою.
2. Що називають спряженням? Які його основні елементи?
3. Що називають ухилом? Як вимірюють величину ухилу? Як позначають ухил на кресленні?
4. Що називають конусністю? Як вимірюють величину конусності? Як позначають конусність на кресленні?
Завдання для самостійної роботи
1. Поділити довільну пряму на п’ять рівних частин.
2. Через довільну точку, взяту на колі діаметром 30 мм, провести пряму, дотичну до цього кола.
3. Побудувати правильний шестикутник, сторона якого дорівнює 25 мм.
4. Побудувати спряження двох прямих (рис. 2.59) радіусом 20 мм. Відмітити центр спряження і точки спряження.
5. Побудувати спряження прямої з колом (рис. 2.60) радіусом 25 мм.


![]()
![]()
Рис. 2.59 Рис. 2.60
7. Накреслити поверхню, конусність якої дорівнює 1:5.
ЛІТЕРАТУРА
Основна
- Михайленко В.Є., Ванін В.В., Ковальов С.М. Інженерна та комп’ютерна графіка: Підручник для студентів вищих закладів освіти / За редакцією В.Є. Михайленко. – К.: Каравела, 2004. – 344 c.
-
Арустамов Х.А. Сборник задач по начертательной геометрии.
М.: Машиностроение, 1978. – 445 с.
Додаткова
- Бубенников А.Н. Начертательная геометрия. – М.: Высшая школа, 1985. – 288 с.
- Верхала А.П., Коваленко Б.Д., Багданов В.М. та ін.. Інженерна графіка: креслення, комп’ютерна графіка за науковою редакцією доктора педагогічних наук, професора А.П. Верхоли. Серія Вища освіта в Україні. – К.: Каравела, 2005. – 301 с.
- Михайленко В.Е., Найдиш В.М. Тлумачення термінів з прикладної геометрії інженерної та комп’ютерної графіки. – К.: Урожай, 1998. – 196 с.
-
Посвянский. Сборник задач по начертательной геометрии. –
М.: Высшая школа, 1978.-320 с.
Навчальне видання
Корх Майя Володимирівна
НАРИСНА ГЕОМЕТРІЯ ТА
ІНЖЕНЕРНА ГРАФІКА
Розділ «Нарисна геометрія»
НАВЧАЛЬНИЙ ПОСІБНИК
Підп. до друку
Формат 60х84/16. Папір офсет. Ум. друк. арк.
Тираж 50 пр. Зам. №
ОНМА, центр «Видавінформ»
65029, м. Одеса, Дідріхсона,8, корп.7
Свідоцтво ДК №1292 від 20.03.2003
Тел./факс:(0482)34-14-12
publish@ma/odessa.ua
1


про публікацію авторської розробки
Додати розробку