Розробка уроку геометрії для 8-го класу на тему "Теорема Піфагора"

8 клас

Без ентузіазму – ніякої математики!

Коли відкриваєш нове, не забувай старого

Навчився сам – навчи двох товаришів.

Мало хотіти, треба діяти!

Чому?!

Математика – гімнастика розуму!

 

Тема уроку: Теорема Піфагора

Мета уроку:

• ознайомити учнів зі змістом теореми Піфагора; показати застосування теореми при розв’язуванні задач;
• розвивати логічне мислення школярів, формувати навики самооцінки;
• виховувати інтерес до історії математики.

Обладнання уроку: комп’ютер, дошка, портрет Піфагора, плакати з усними вправами, малюнки до задач, картки для практичних робіт, математичне лото.

Тип уроку: урок засвоєння знань та умінь.

Методи і прийоми: пояснювально-ілюстративний метод, метод запитань і відповідей, наочний метод, словесний метод (бесіда, розповідь, діалог), постановка проблемних запитань, пошуковий метод.

Форми організації діяльності учнів: колективна форма роботи (фронтальне опитування, усна робота), індивідуальна робота (картки, кросворд).

 

Хід уроку

І. Організаційний момент.

Вчитель: Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання і нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір.

Пам 'ятка для учня

1.       Будь уважним.
2.       Активно пізнавай та аналізуй нове.
3.       Самостійно встановлюй зв'язки відомого з невідомим.
4.       Учись відчувати радість відкриття.

 

Я сподіваюсь на нашу співпрацю, свідоме засвоєння матеріалу уроку. Запишіть, будь-ласка, число, класна робота.

 У кулачному бою на  58-й Олімпіаді, яка проходила в 548 році до н.е. брав участь один із давньогрецьких математиків. Переказують, що через малий зріст судді не хотіли допускати його до змагань.

 - Можливо, - заперечив молодий вчений, - мій вигляд і не викликає у вас довіри. Але я буду наносити удари з такою математичною точністю, що супротивникові стане жарко. Моя глибока віра в число – це моє життєве кредо.

 І він додержав свого слова – став чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах.

 То ж нехай його слова: „Тимчасова невдача краща від тимчасової удачі” стануть девізом нашого уроку.

 

ІІ. Повідомлення теми уроку.

         Сьогодні на уроці я пропоную вивчити: теорему нареченої, теорему німфи, теорему метелика, теорему 100 биків, розглянути «втечу убогих» і «міст ослів».

У вас може виникнути запитання: чому так багато теорем на один урок? Цілком вірно: ці назви стосуються всього однієї теореми.

Щоб дізнатися про її автора, ви повинні розгадати кросворд та у виділеній частині прочитати закодоване слово.

Кросворд

			1
		2
			3
		4
	5
6
		7

 

1. Як називаються трикутники, сторони яких відповідно пропорційні?

2. Як називається відрізок, що виходить з вершини кута трикутника і ділить його навпіл?

3. Ім’ям якого вченого названо теорему: якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні?

4. Сторона прямокутного трикутника.

5. Хорда ділить коло на дві … .

6. Як називається сторона трикутника, що лежить проти прямого кута?

7. Як називається чотирикутник, у якого дві протилежні сторони паралельні?

Відповіді. 1. Подібні. 2. Бісектриса. 3. Фалес. 4. Катет. 5. Дуги. 6. Гіпотенуза. 7. Трапеція.

Закодоване слово: Піфагор.

Отже, ми сьогодні маємо вивчити теорему Піфагора.(записати тему у зошит!!!)

 ІІІ. Актуалізація опорних знань та умінь.

Вправа „Мозковий штурм”:

1. Який трикутник називають прямокутним?

2. Сформулюйте властивість катета, що лежить проти кута в 30⁰.

3. Продовжити речення:

• сума кутів у трикутнику дорівнює....
• кут, що дорівнює 90⁰ називають ....
• сума двох гострих кутів прямокутного трикутника дорівнює....
• сторони прямокутного трикутника, які утворюють прямий кут, називають ...

ІV.  Сприйняття й первинне усвідомлення нового матеріалу

1. Вступне слово вчителя.

Теорема Піфагора — одна з основних у евклідовій геометрії. Завдяки їй можна довести більшість тео­рем геометрії та розв'язати не одну задачу. Легенда стверджує, що Піфагор після відкриття цієї теореми на знак глибокої вдя­чності богам здійснив гетакомбу — приніс в жертву аж сто биків. Зрештою інші автори подібний вчинок приписують Фалесу за ві­дкриття ним того, що вписаний кут, який спирається на діаметр, є прямим. Як би там не було, але теорема Піфагора — справді фундаментальний геометричний факт, на якому базується уся теорія вимірювання геометричних фігур (їх довжин, площ і об'є­мів). Тому її потрібно добре засвоїти.

2. Усний журнал.

Двоє учнів підготували історичні відомості про Піфагора та теорему, що носить його ім'я. Вони розповідають їх класу.

Учень. Піфагор жив у VI ст. до н.е. в Давній Греції. Він народився близько 580 р. до н.е. на острові Са­мос. Батьком Піфагора був Мнесарх, різьбяр по кош­товних каменях. Ім'я матері Піфагора невідоме.

Учениця. Піфагор багато подорожував, його ім'я було оточене багатьма легендами, тому тепер важ­ко визначити, що зробив він сам, а що запозичив у інших. Залежність між сторонами прямокутного трикутника була відома ще за 1000 років до Піфагора в Давніх Вавилоні та Єгипті. Піфагору, оче­видно, належить доведення цієї теореми і широке застосування її під час розв'язування задач.

Учень. Землеміри Стародавнього Єгипту для побудови прямого кута чинили так. Мотузок діли­ли вузлами на 12 рівних частин і кінці зв'язували. Потім мотузок натягували на землі так, щоб утво­рився трикутник із сторонами 3, 4 і 5 поділок.

 

Кут трикутника, протилежний стороні, яка має 5 поділок, був прямий. Тому прямо­кутний трикутник із сторонами 3, 4, 5 одиниць називають єгипетським або піфагоровим.

 

 

 

 

3. Вивчення теореми Піфагора

Практична робота: (учні отримують картки) (Додаток 1)

Завдання:

1. ^{Виміряйте довжини всіх сторін трикутника.}
2. ^{Обчисліть квадрати довжин сторін.}
3. ^{Знайдіть суму квадратів катетів.}
4. ^{Порівняйте знайдену суму із квадратом гіпотенузи.}
5. ^{Зробіть висновок.}

 Вчитель. У всіх вийшло, що a² + b² = с² ?

Цю закономірність і виражає теорема Піфагора, якій присвячений наш урок. «Квадрат гіпотенузи дорівнює сумі квадратів катетів» саме так звучить ця теорема.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отже, теорема Піфагора – це теорема, яка відображає зв’язок між катетами і гіпотенузою в прямокутному трикутнику.

V. Робота за теоремою Піфагора.

1.     Розв'язування задач за готовими рисунками.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

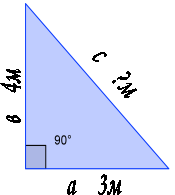
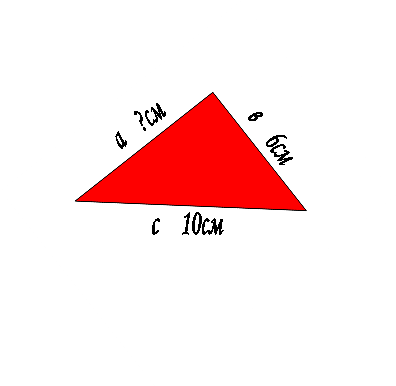
3. Фізкультхвилинка для зняття втоми з очей.

 

 

Вчитель. А чи потрібна теорема Піфагора в житті? Давайте подивимось.

VІ. Формування практичних умінь

1. Розв’язування задач (використовуються малюнки до задач).

Ці задачі не прості,

Застосуєш їх в житті.

Щоб їх добре розв'язати,

Геометрію потрібно знати.

 

А) Знайдіть довжину приставленої до будинку драбини, якщо нижній кінець знаходиться на відстані 3 м від будинку, а верхній – на стику стіни й даху. Висота стіни будинку дорівнює 4 м.

 

 

 

 

 

 

 

 

 

 

 

Дано: ∆ АВС, С = 90⁰, АС= 3 м, ВС= 4 м

 Знайти: АВ

Розв’язання

 АВ – гіпотенуза ∆ АВС. За теоремою Піфагора АВ² = АС² + ВС²; АВ² = 3² + 4² = 9+ 16 = 25. АВ = = 5 (м).

 Відповідь. 5 м.

 Б) Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ₁ однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб ялинка стояла вертикально.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( АВ =

 

 В) Розрахуйте необхідну довжину електричного проводу, який треба провести від дому висотою 2,5 м, до стовба - висотою 8,5 м. (Відстань між об'єктами 8 м)

 

 

 

 

 

 

 

 

 

 

 

 

Відповідь: 10 м.

 

Г) Задача індійського математика ХІІ ст. Бхаскари.

 

 

 

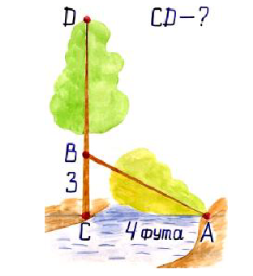
"На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка,

Верхушка склонилась у края реки,

Осталось три фута всего от ствола.

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?"

 

Відповідь: 8 футів

 

2. Вправа „Оціни себе”.

Тест

 1. Як називаються сторони прямокутного трикутника, які утворюють гострий кут?

   а) катети     б) гіпотенуза        в) катет і гіпотенуза  г) два катети і гіпотенуза

 2. Як читається теорема Піфагора?

 а) квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його катетів

 б) квадрат гіпотенузи прямокутного трикутника дорівнює різниці квадратів його катетів

 в) гіпотенуза прямокутного трикутника дорівнює сумі катетів

 г) с² = а² – в²

3. Як називають прямокутний трикутник, сторони якого дорівнюють 3 м,   4 м, 5м?

   а) вавілонський     б) єгипетський        в) індійський

 

 4. Катети прямокутного трикутника дорівнюють 5 і 12 см. Чому дорівнює гіпотенуза трикутника?

                  а) 15 см         б) 14 см         в) 13 см            г) 16 см

 5. Гіпотенуза прямокутного трикутника дорівнює 10 см, а один з катетів 8 см. Чому дорівнює другий катет?

                  а) 25 см          б) 6 см            в) 5 см             г) 1 см

 

VІІ. Домашнє завдання: вивчити п.16, ст. 116, повторити п.15, ст 113.

 Середній рівень: № 529

  Достатній рівень: № 529, 533.

               

VІІІ. Підведення підсумків уроку.

• Яке відкриття ми сьогодні зробили?
• Хто зможе нагадати, як формулюється теорема Піфагора?
•   Яку практичну користь дає нам теорема Піфагора?
•   До яких трикутників застосовують теорему Піфагора?

 

Отже, сьогодні ви познайомилися з найвідомішою теоремою планіметрії – теоремою Піфагора. Тому люди пам'ятають Піфагора дві з половиною тисячі років. Ось чому серед знаменитих олімпійських чемпіонів він довго залишиться найвідомішим, тому що йому випало щастя перемогти не тільки супротивників, але й перемогти час.

Діти, попереду у вас ще багато різних теорем життєвих та геометричних. Можливо, з часом теорема Піфагора буде здаватися вам дуже простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему – теорему Піфагора, – цікаву, могутню, вічну.

А закінчити урок я хочу словами:

Життя – театр, а всі ми в нім актори,

Ми знаємо багато різних див,

Та пам’ятати будем Піфагора,

Що теорему «золоту» створив.

Ось і закінчився наш урок.

Час невпинно й швидко так летить.

Ви до знань зробили новий крок.

Хай у всьому завжди вам щастить!

Дякую, що працювали гарно,

Часу ви не витрачали марно,

Дякую за дисципліну на уроці

І бажаю успіхів у цьому  році!

Оцінювання відповідей учнів, коментоване оголошення оцінок за урок.

(Додаток 1)

Практична робота                     

 

^{1. Виміряйте довжини всіх сторін.}

^{2. Обчисліть квадрати довжин сторін.}

^{3. Знайдіть суму квадратів катетів.}

^{4. Порівняйте знайдену суму із квадратом гіпотенузи.}

^{5. Висловіть своє припущення.}

Катет: а		а²		а² + в²
Катет:  в		в²
Гіпотенуза: с		с²