Урок "Площа прямокутника" (Геометрія 8 клас)

Про матеріал

Пропоную розробку уроку з геометрії з теми "Площа прямокутника". До уроку розроблена презентація, яка доповнює урок, підібрано цікаві задачі, розроблено кросворд до уроку. Матеріали будуть корисними вчителям математики.

Перегляд файлу

Тема уроку: Поняття площі. Площа прямокутника.

Мета уроку: дати поняття площі, визначити властивості площі, вивести формулу для знаходження площі прямокутника, прямокутного трикутника;

розвивати логічне мислення, інтелектуальні і творчі здібності учнів, вміння робити висновки, пізнавальну активність;

формувати математичну та інформаційну компетентність;

виховувати старанність, працьовитість, наполегливість, свідоме ставлення до навчання.

Тип уроку: урок формування нових знань.

Методи: бесіда з елементами розповіді, інформаційно-комунікаційні, евристичні, практичні.

Обладнання: комп’ютер, проектор, екран.

Хід уроку

I. Організаційний етап

Перевірка готовності учнів до уроку, наявність зошитів, приладдя.

II. Актуалізація опорних знань

Урок супроводжується презентацією.

Епіграф:
«Предмет математики настільки серйозний, що не можна втрачати нагоди зробити його трішки цікавішим» Блез Паскаль

Сьогодні випала саме така нагода, бо математика є дивовижною вчителькою в мистецтві спрямовувати думки, наводити порядок, викорчовувати безглуздя. Мислити правильно потрібно всім: і робітникові, і інженерові, і вченому, і художнику, і архітектору, і поету.

Задача. Ремонтуючи клас влітку, необхідно було розрахувати кількість фарби для підлоги. Скільки потрібно банок по 2,8 кг, якщо на 1 м² приблизно витрачається 120 г фарби.

Що необхідно, щоб розв’язати цю задачу? Правильно, знати площу підлоги. Якщо довжина класу 11 м, а ширина 6 м, то площа 66 м². Отже, потрібно 120 г * 66 м²= 7920 г = 7,92 кг фарби. А банок потрібно 7,92 : 2,8  2,82  3!

ІІІ. Оголошення теми і мети уроку

Отже, тема уроку: Площа. Площа прямокутника.

На уроці ми визначимо властивості площі, виведемо формулу для знаходження площі прямокутника, прямокутного трикутника; розв’яжемо задачі на знаходження площі. Будьте старанні, наполегливі, відповідальні.

IV. Засвоєння нового матеріалу

Будь-який плоский многокутник займає частину площини. Якщо цю частину площини виразити деяким числом, то дістанемо площу многокутника. Площу позначають буквою S.

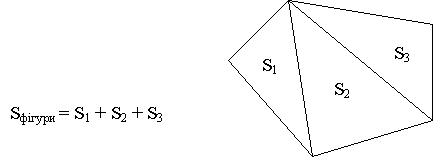Зрозуміло, що площа будь-якої фігури дорівнює сумі площ частин, з яких вона складається.

З попередніх класів ви знаєте, що площу квадрата зі стороною а можна обчислити S = a².

Будемо вважати формулу площі квадрата основною і приймемо її без доведення. Для інших фігур формули площі треба виводити, спираючись на основні властивості площі. Сформулюємо їх.

Площа – це додатна величина.
Рівні фігури мають рівні площі.
Якщо фігура розбивається на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площ її частин.
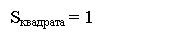
Площа квадрата зі стороною, що дорівнює одиниці вимірювання, дорівнює одиниці.

Одиниці вимірювання площі коротко записуємо так: 1 см² або 1 м².

Деякі одиниці вимірювання площі мають спеціальні назви: ар ( площа квадрата зі стороною 10 м), гектар (площа квадрата зі стороною 100 м), 1 а = 100 м² (ар ще називають «сотка»), 1 га = 10000 м², 1 акр = 4047 м². Аруру – антична міра виміру площі, аруру = 0,024 га.

Математики придумали власну жартівливу одиницю для вимірювання жіночої краси – міліелен. Свою назву одиниця краси отримала на честь Єлени Троянської (найгарнішою з жінок, через яку розгорілася однойменна війна) а визначається як «кількість краси, достатню для того, щоб запустити одне судно». Якщо вірити Гомеру, заради самої прекрасної Єлени спустили на воду аж 1186 суден з цілою армією озброєних до зубів воїнів.

Площа прямокутника

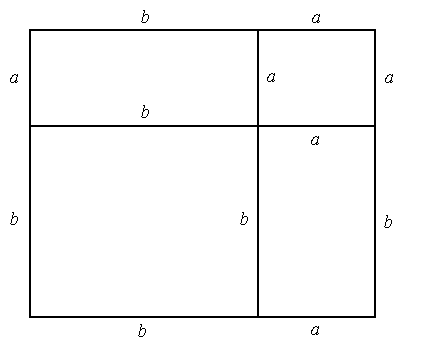
S = ab.

Доведемо цю формулу

Добудуємо даний прямокутник до квадрата зі стороною а + b. Тоді площа квадрата можна знайти S = (а + b)².

З іншого боку площа квадрата складається із площ двох квадратів зі сторонами а і b і площ двох рівних прямокутників зі сторонами а і b.

S_{квадрата} = 2S_{прямокутника} + a² + b².

Отже, (а + b)² = 2S_{прямокутника} + a² + b², або а² + 2аb + b² = 2S_{прямокутника} + a² + b².

Звідси, S_{прямокутника} = ab.

Прямокутний трикутник це половина прямокутника, тобто діагональ прямокутника ділить його на два рівних прямокутних трикутника, з катетами а і b.

Тому площу прямокутного трикутника можна знайти за формулою S = .

Якщо фігури мають рівні площі, то такі фігури називаються рівновеликими.

V. Практичне закріплення вивченого матеріалу

1. Сторони квадратів 100 м і 150 м. Знайдіть сторону третього квадрата, площа якого дорівнює сумі площ двох заданих.

Дано: а₁ = 100 м, а₂ = 150 м;

S₃ = S₁ + S₂.

Знайти: а₃.

Розв’язання

S₁ = 100² = 10000 (м²), S₂ = 150² = 22500 (м²), S₃ = 10000 + 22500 = 32500 (м²).

а₃ = √32500 = 50√13 ≈ 180 (м).

Відповідь: 50√13 ≈ 180 м.

2. Знайти сторони прямокутника, якщо його периметр 74 см, а площа 3 м².

Дано: АВСD - прямокутник;

Р = 74 дм,

S = 3 м².

Знайти: сторони.

Розв’язання.

Позначимо сторони АВ = а, ВС = b, тоді складемо і розв’яжемо систему рівнянь:

2(а + b)2 = 74, а + b = 37, а = 37 – b,

аb = 300; аb = 300; b(37 – b) = 300;

Розв’яжемо квадратне рівняння: b² – 37b + 300 = 0, b₁ = 12, або b₂ = 25.

b₁ = 12, або b₂ = 25,

а₁ = 25, або а₂ = 12.

Отже, сторони прямокутника 12 дм і 25 дм.

Відповідь: 12 дм, 25 дм.

3. Україна – одна з найбільших європейських держав, її площа 604 тис. км². На скільки квадратних кілометрів площа України більша за площу Франції (544 тис. км²), Швеції (450 тис. км²)?

Відповідь: на 60 тис. км², на 154 тис. км².

4. Сад має форму прямокутника із сторонами 80 і 25 м. Половину усієї площі засаджено яблунями. Для кожної яблуні відведено 40 м². Скільки яблунь у саду?

Відповідь: 50 яблунь.

5. Щоб посіяти гречку на 1 м² потрібно 15 г гречки. Скільки грамів гречки потрібно, щоб засіяти ділянку 40 м²?

Відповідь: 600 г.

6. Знайдіть площу заштрихованої частини квадрату, сторона якого 4 см.