Розробка уроку на тему "Множення многочлена на многочлен".

7 клас      Алгебра

 

Тема уроку. Множення многочлена на многочлен.

Мета уроку. Продовжити формувати вміння і навички множення многочлена на многочлен; розвивати логічне мислення, уважність, vпeвнeнicть у власних силах; виховувати активність, бажання здобувати знання та формувати в учнів різні групи компетенцій:

1. Соціальні — бути готовим до самостійного пошуку розв"язання проблеми, прояву ініціативи, формувати вміння проводити бесіду;
2. Полікультурні - розвиток уміння застосовувати отримані знання на практиці; опанувати засади культурного спілкування в ході обговорення питань уроку, розвивати вміння вести групову бесіду; робити висновки;
3. Інформаційні - одержання додаткової інформації з історії розвитку математики та уміння використовувати її, розширення кругозору;
4. Самоосвітні та саморозвиваючі — удосконалювати вміння школяра працювати з книгою, розвивати готовність навчатися, пам"ять, увагу, творчий підхід до вирішення проблеми.

Тип уроку : формування вмінь і навичок.

Обладнання: карточки із завданнями, кольорова крейда, портрет

Георгія Вороного та Ісаака Ньютона, таблиця   «Многочлени».

Підручник: Істер О.С. Алгебра : Підручник для 7 кл. загальноосвіт.

навч. закл. - К.: Генеза. 2015-256с.

Девіз уроку: " Знати , мислити, вміти, діяти"

Хід уроку

І. Перевірка домашнього завдання.

1. Черговий перевіряє наявність домашнього завдання.
2. Відповіді до прикладів з домашнього завдання написано на дошці зазделегідь. Учні здійснюють самоперевірку.
3. Повторення теоритичних питань. Інтерактивна вправа " Мікрофон".

•         Який вираз називають одночленом ?
•          Що називають степенем одночлена ?
•          Дайте означення многочлена.

•               Що називають членами многочлена ?
•               Які члени многочлена називають подібними?
•                    Що називають степенем многочлена?
•                   Сформулюйте правило множення многочлена на многочлен?
•               Як множать більше ніж два многочлени?

4. Прочитай записи по різному:

а) (а + b)(с —d);

б) ( а + b ) с .

II. Мотивація навчальної діяльності та повідомлення теми уроку.

Відомий давньогрецький філософ і вчений Арістотель ( 384 — 322 до н.е) сказав : " Розум полягає не тільки в знанні, але й в умінні застосовувати знання до справи".

На сьогоднішньому уроці, який буде присвячений многочлену, ви це покажете. Ми з вами розв"яжемо вправи на множення многочленів, дізнаємося про історію цього терміну та про зв"язок алгебри і геометрії. Я хочу сказати , що дана тема про дії над многочленами є фундамен­тальною у формуванні вмінь виконувати тотожні перетворення алгебраїчних виразів у 7 класі. А також є складовим компонентом у завданнях на перетворення цілих виразів у 8 класі. Повідомлення теми уроку.

III. Формування вмінь і навичок розв'язування вправ.

Інтерактивна частина.

1. Робота у міні - групах:

а) Кожна група отримує картку, яку треба заповнити . Після розв'язання отриманих вправ, групи по колу міняються картками . Друга група перевіряє роботу першої групи і виправляє помилки, після чого картки здаються вчителю, а перша - другої.

Зразок картки

 Заповнити таблицю

№ п/п		Назва	Степінь	Коефіцієнти
1.
2.	7
3.
4.
5.
6.

 

б) Заповніть порожні клітинки ( умови записані на дошці):

(І група): (a + b)(с-d) =____-ad+bc____bd

(II група): (3 m-р )(m + р ) = 3­­­­____+3mp____-p

 

Після виконання , представник від групи заповнює клітинки на дошці

 в) Знайдіть помилку в розв'язанні та наведіть правильне розв"язання:

І група: (с-8)(d + 1 ) = сd-8 с + с + 8d + 8

II група : ( а + аb-b) (а-b) = 2а+ ab+ 2 аb - 2аb - аb- 3b

г) Виконайте дії та виберіть правильну відповідь:

(а + b)(-а+аb-b)

 Відповідь: а) а +  2а² b-2ab²- b³

б) -а³- 2аb +2ab + b

в) а³+ b³

г) - а - b

2.               Творче завдання.

( ∆ + O)(□ + ♣) =

3.               " Мозковий штурм "

Поясніть зміст формули

*(а + b)(с + d) = ас + bс + аd + bа, використовуючи даний малюнок.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

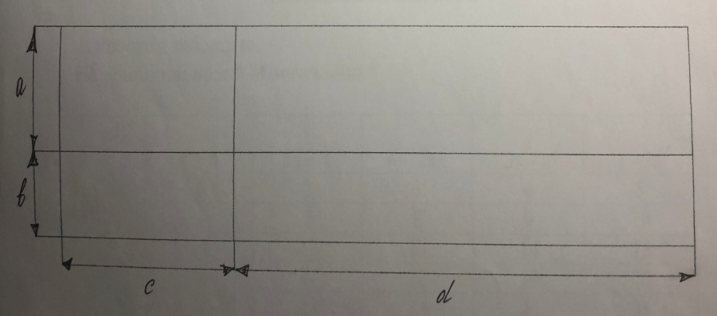
Пропоную всім висловити свої ідеї, коментарі. Усі пропозиції записуються на дошці в порядку їх оголошення. На закінчення обговорюємо й оцінюємо запропоновані ідеї, робимо висновок.

Висновок : Це геометрична інтерпретація множення многочленів. З малюнка видно, що площа прямокутника із сторонам (а + b)і(с+d )дорівнює сумі площ чотирьох прямокутників, які відповідно дорівнюють ас, аd, bс і bd. Проте таким способом можна ілюструвати цю рівність лише для додатних чисел.

Цей запис показує практичне застосування алгебри та геометрії. Він ілюструє тісний зв"язок цих двох наук.

4. Звіт про виконання творчого завдання .

а) Історична довідка про множення многочленів .

Формули множення многочленів стародавні вавилоняни знали ще 4000 років тому, але тоді ще не існувало установленого тепер символічного запису, тому ці формули були виражені словесно. Та й взагалі алгебраїчні задачі вони розв'язували геометрично, подаючи величини у вигляді прямолінійних відрізків. Добуток чисел ав розглядали як прямокутник зі сторонами завдовжки а і в, число а - як квадрат із стороною а і т.д. Такі словесні записи були громіздкими, а тому їх використання гальмувало розвиток алгебри як науки.

Лише в XVIII ст. Ньютон першим серед видатних учених повністю відмовився від геометричної алгебри, реформувавши її на новій сучасній основі.

б) Різні способи множення многочленів.

Записувати множення многочленів можна по - різному. Найчастіше компоненти записують у рядок, як ми це робили.

Але варто знати ,що многочлени також можна множити в стовпчик, наприклад:

                                                    

                                                   

А зараз ознайомтеся як множити многочлен на многочлен за допомогою таблиці:

		x	-1
X 2		2x	-x -2

 

Завдання : виконайте множення многочлена на многочлен одним із вказаних способів.

 

в) Спосіб роботи з літературою.

Ще зі студенських років відомий математик Єрмаков В.П. виробив оригінальний спосіб роботи з науковою літературою, завдяки якому він міг швидко орієнтуватися в найскладніших питаннях математики і робити самостійні відкриття в різних її галузях. Він спочатку читав вступ до твору, щоб дізнатися, які положення буде доводити автор, потім із закінчення дізнавався, чого автор досяг, і нарешті, зазирнувши десь посередині твору, виявляв, яким методом користувався автор у своїх дослідженнях. Потім закривав твір, і якщо досліджуване питання, на його думку було варте уваги, сам намагався добути всі результати самостійно. Користуючись цим методом, вчений, опрацювавши кілька фундаментальних творів, написав блискучі оригінальні праці.

Єрмаков В.П. запропонував читачам видання "Журнал элементарной математики" написати твір на тему " Розкладання многочленів на множники..." Кращим виявився твір учня Прилуцької гімназії Георгія Вороного , який і було надруковано в другому томі журналу. Успіх окрилив юнака і визначив життєвий шлях майбутнього математика.

Виконання вправ іі підручника.

а) Фронтально ( один учень біля дошки ) № 346;

б) Колективне розв'язування №348

в) Коментоване розв'язування № 350

Індивідуальне завдання

Робота з таблицею. На дошці таблиця Многочлени

В А	а + 4	5а+1	а— 2ах		1-2а
2а- 3	1	2	3	4	5
5а +1	6	7	8	9	10
а + 2х	11	12	13	14	15
	16	17	18	19	20
2х-5а	21	22	23	24	25

 

Кожен учень виконує індивідуальне завдання самостійно під тим номером, під яким його прізвище записано у класному журналі.

Завдання. Виконати множення многочленів.

Наприклад. Учень під № 1 виконує завдання (2а-3)*(а + 4).

ІY.Підсумок уроку

Рефлексивна бесіда

На аркушу паперу, що передається з парти на парту, прошу намалювати довільну геометричну фігуру в тому місці, яке відображає ваше розуміння теми на уроці.

 

 

1. Ми сьогодні повторили...

2. Ми сьогодні виконували...

3. Ми сьогодні дізналися ...

4. Що викликало найбільшу цікавість ?

V. Повідомлення домашнього завдання.

Повторити §9-11, виконати № 345, 349.

Творче завдання. Виконати множення двох довільних двочленів у стовпчиик або за допомогою таблиці.

Використана література

1. Учитель року - 2004. Цикли уроків з математики. - X.:" Основа", 2005.

2. Конфорович А Г, У пошуках інтеграла. - К.: Рад. Шк., 1990.

3. Алгебра. Пробные учебники для 6-8 классов средней школы. Матер, для ознакомления М.: Просвещение, 1981.

4. Бевз Г.П. Методика викладання алгебри. Посіб. для вч. - К | Рад. Шк 1971.